HEURISTIC ALGORITHMS FOR A JOBSHOP PROBLEM WITH MINIMIZING

HEURISTIC ALGORITHMS FOR A JOB-SHOP PROBLEM WITH MINIMIZING TOTAL JOB TARDINESS Yuri N. Sotskov 1, Omid Gholami 2, Frank Werner 3 1. United Institute of Informatics Problems, Minsk, Belarus, e-mail: sotskov@newman. bas-net. by 2. Islamic Azad university - Mahmudabad Branch, Mahmudabad, Iran, e-mail: gholami@iaumah. ac. ir 3. Faculty of Mathematics, Otto-von-Guericke-University, Magdeburg, Germany , e-mail: frank. werner@ovgu. de OPTIMA 2012, Costa da Caparica, Portugal September 23 -30, 2012 1

OUTLINE OF THE TALK Introduction Literature Review for Single-Track Railway Systems Problem Setting in Terms of a Job-Shop Mixed (Disjunctive) Graph Formulation of a Job-Shop Scheduling Problem Heuristic Algorithms Computational Results 2
INTRODUCTION Train road map in Belarus 3

LITERATURE REVIEW FOR SINGLE-TRACK RAILWAY PROBLEMS Szpigel (1973): B&B algorithm, results for 5 sections and 10 trains Cai and Goh (1994): greedy algorithm Carey and Lockwood (1995): binary mixed integer programming model Mladenovic and Cangalovic (2007): constraint programming approach Zhou and Zhong (2007): B&B algorithm, resource-constrained project scheduling problem Liu and Kozan (2011): no-wait condition for prioritized trains, recursive procedure Sotskov and Gholami (2012): shifting bottleneck procedure 4

PROBLEM SETTING IN TERMS OF A JOB-SHOP set of railroad sections (machines) ◦ M ={ M 1, M 2, …, Mm } set of trains (jobs) ◦ J ={ J 1, J 2, …, Jn } the sequence of the job operations on the corresponding machines is given for any job Ji : ◦ Oi = (Oi 1 , Oi 2 , … , Oini ) 5
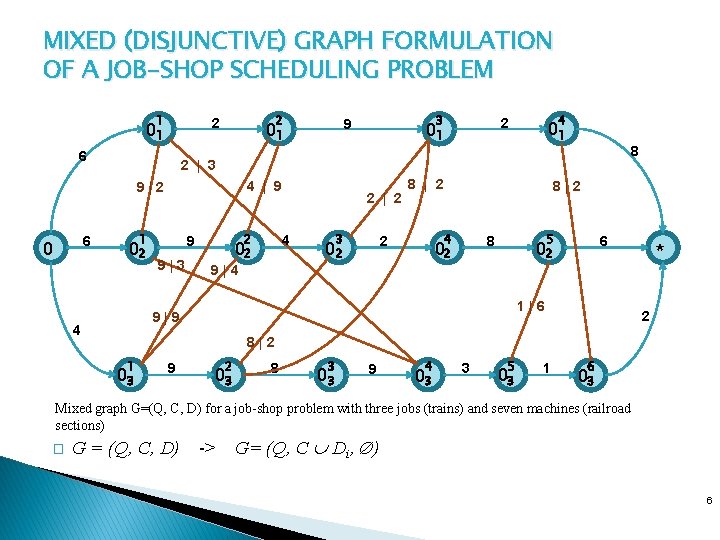
MIXED (DISJUNCTIVE) GRAPH FORMULATION OF A JOB-SHOP SCHEDULING PROBLEM 1 2 2 01 6 6 4 2 01 01 8 2 | 3 4 | 9 9|2 0 3 9 01 1 02 2 9 9|3 4 02 9|4 2 | 2 3 8 | 2 4 2 02 8|2 5 8 02 1|6 9|9 4 6 02 * 2 8|2 1 03 9 2 03 8 3 03 9 4 03 3 5 03 1 6 03 Mixed graph G=(Q, C, D) for a job-shop problem with three jobs (trains) and seven machines (railroad sections) � G = (Q, C, D) -> G= (Q, C Di, Ø) 6

HEURISTIC ALGORITHMS Algorithms: � � � Ordinal-algorithm Max. PT-algorithm Min. PT-algorithm Priority rules for comparing conflict jobs: � � � Release time Completion time Due date 7
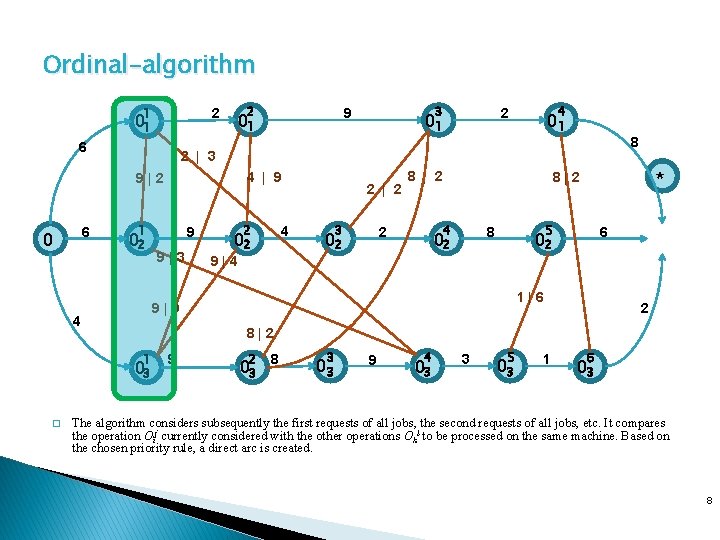
Ordinal-algorithm 1 2 01 6 2 6 4 | 9 1 02 9 9|3 2 4 02 9|4 2 | 2 01 3 8 | 2 8 4 2 02 * 8|2 5 8 02 6 02 1|6 9|9 4 2 8|2 1 03 � 4 2 01 2 | 3 9|2 0 3 9 01 9 2 03 8 3 03 9 4 03 3 5 03 1 6 03 The algorithm considers subsequently the first requests of all jobs, the second requests of all jobs, etc. It compares the operation Oij currently considered with the other operations Okl to be processed on the same machine. Based on the chosen priority rule, a direct arc is created. 8
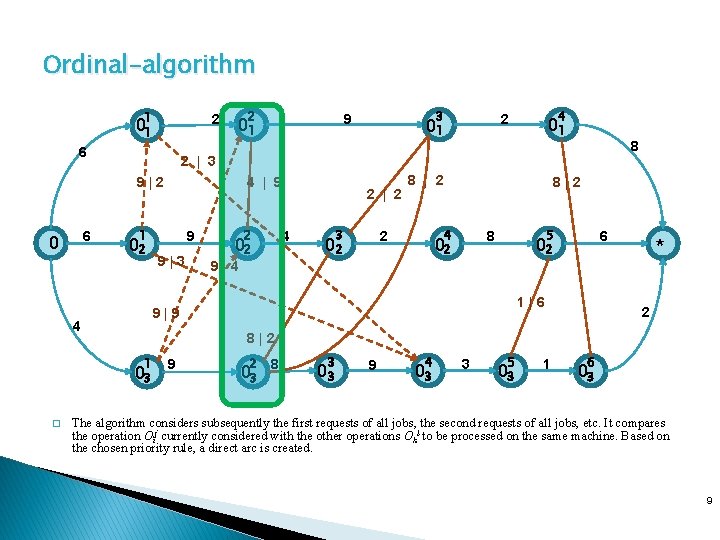
Ordinal-algorithm 1 2 01 6 2 6 4 | 9 1 02 9 9|3 2 4 02 9|4 2 | 2 01 3 8 | 2 8 4 2 02 8|2 5 8 02 6 02 1|6 9|9 4 * 2 8|2 1 03 � 4 2 01 2 | 3 9|2 0 3 9 01 9 2 03 8 3 03 9 4 03 3 5 03 1 6 03 The algorithm considers subsequently the first requests of all jobs, the second requests of all jobs, etc. It compares the operation Oij currently considered with the other operations Okl to be processed on the same machine. Based on the chosen priority rule, a direct arc is created. 9
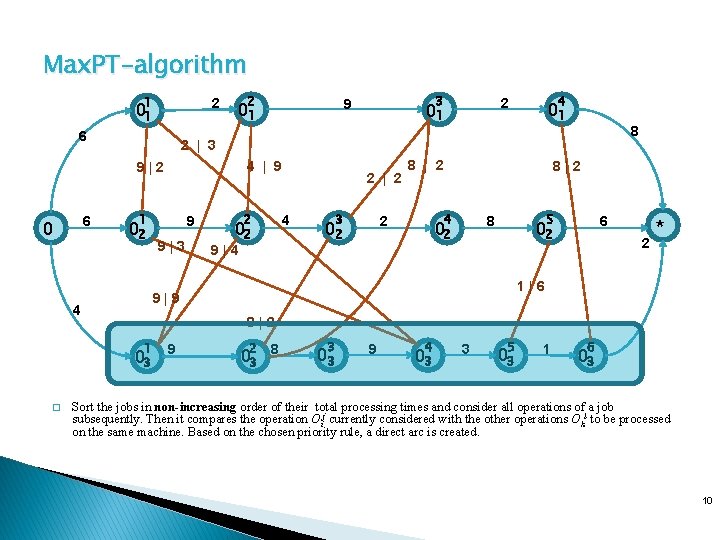
Max. PT-algorithm 1 2 01 6 2 6 4 | 9 1 02 9 9|3 2 4 02 9|4 2 | 2 01 3 8 | 2 8 4 2 02 8|2 5 8 02 6 02 2 * 1|6 9|9 4 8|2 1 03 � 4 2 01 2 | 3 9|2 0 3 9 01 9 2 03 8 3 03 9 4 03 3 5 03 1 6 03 Sort the jobs in non-increasing order of their total processing times and consider all operations of a job subsequently. Then it compares the operation Oij currently considered with the other operations Okl to be processed on the same machine. Based on the chosen priority rule, a direct arc is created. 10
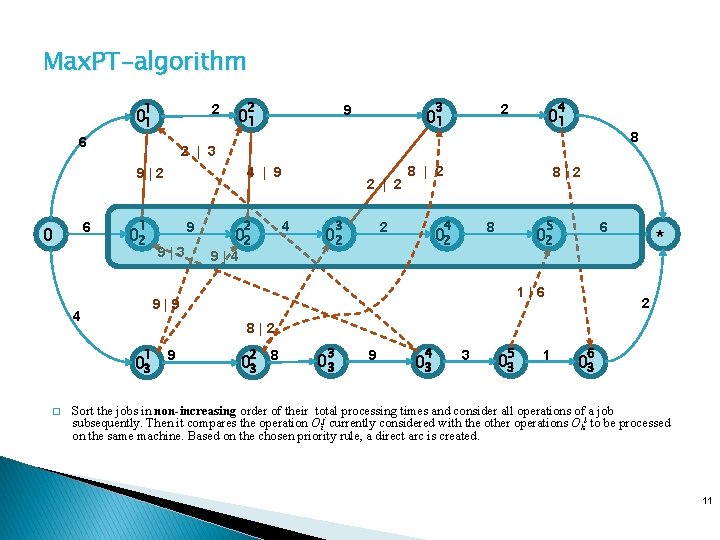
Max. PT-algorithm 1 2 01 6 2 6 4 | 9 1 02 01 9 9|3 2 4 02 9|4 2 | 2 3 8 | 2 8 4 2 02 8|2 5 8 02 6 02 1|6 9|9 4 * 2 8|2 1 03 � 4 2 01 2 | 3 9|2 0 3 9 01 9 2 03 8 3 03 9 4 03 3 5 03 1 6 03 Sort the jobs in non-increasing order of their total processing times and consider all operations of a job subsequently. Then it compares the operation Oij currently considered with the other operations Okl to be processed on the same machine. Based on the chosen priority rule, a direct arc is created. 11
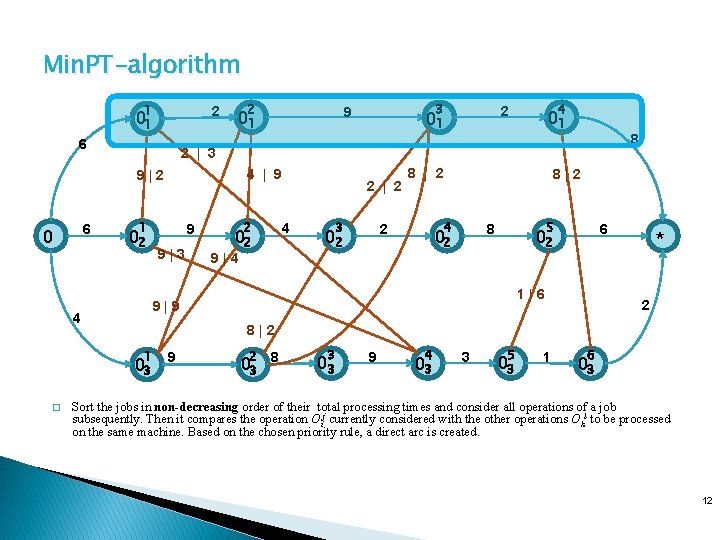
Min. PT-algorithm 1 2 01 6 2 6 4 | 9 1 02 9 9|3 2 4 02 9|4 2 | 2 01 3 8 | 2 8 4 2 02 8|2 5 8 02 6 02 1|6 9|9 4 * 2 8|2 1 03 � 4 2 01 2 | 3 9|2 0 3 9 01 9 2 03 8 3 03 9 4 03 3 5 03 1 6 03 Sort the jobs in non-decreasing order of their total processing times and consider all operations of a job subsequently. Then it compares the operation Oij currently considered with the other operations Okl to be processed on the same machine. Based on the chosen priority rule, a direct arc is created. 12
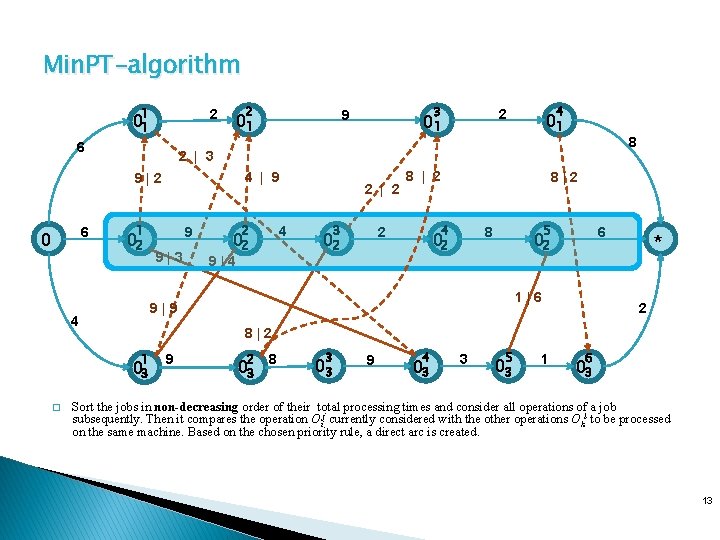
Min. PT-algorithm 1 2 01 6 2 6 4 | 9 1 02 9 9|3 2 4 02 9|4 2 | 2 01 3 8 | 2 8 4 2 02 8|2 5 8 02 6 02 1|6 9|9 4 * 2 8|2 1 03 � 4 2 01 2 | 3 9|2 0 3 9 01 9 2 03 8 3 03 9 4 03 3 5 03 1 6 03 Sort the jobs in non-decreasing order of their total processing times and consider all operations of a job subsequently. Then it compares the operation Oij currently considered with the other operations Okl to be processed on the same machine. Based on the chosen priority rule, a direct arc is created. 13
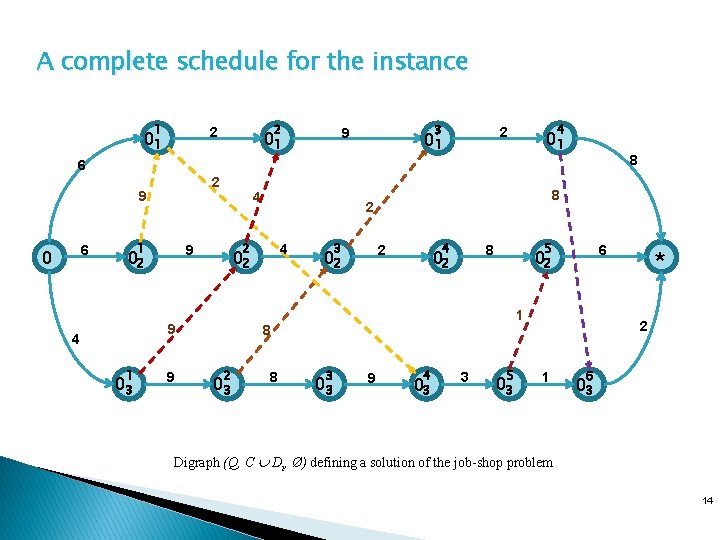
A complete schedule for the instance 1 2 2 01 3 9 01 4 2 01 01 8 6 2 9 6 0 1 4 2 9 02 4 1 03 9 4 02 9 8 2 3 4 2 02 5 8 02 1 8 2 03 8 6 02 3 03 9 4 03 3 5 03 * 2 1 6 03 Digraph (Q, C Di, Ø) defining a solution of the job-shop problem 14
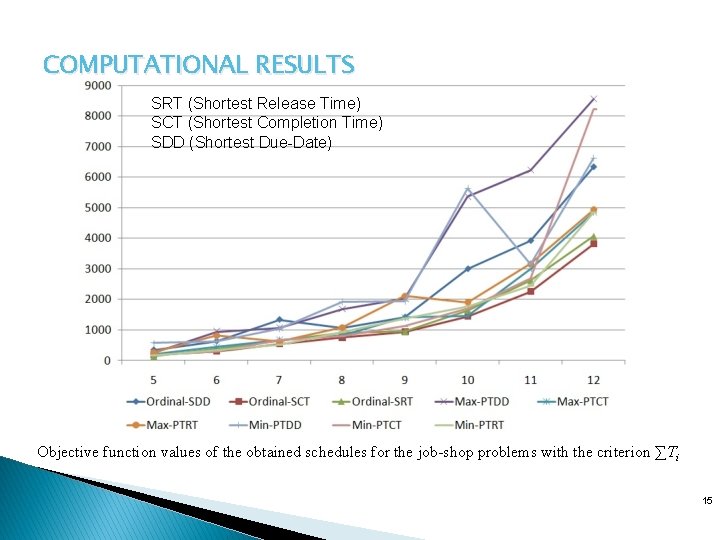
COMPUTATIONAL RESULTS SRT (Shortest Release Time) SCT (Shortest Completion Time) SDD (Shortest Due-Date) Objective function values of the obtained schedules for the job-shop problems with the criterion ∑Ti 15
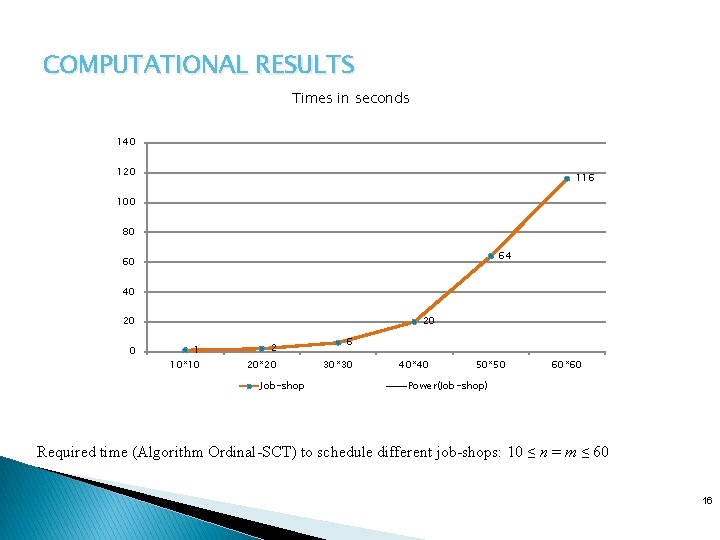
COMPUTATIONAL RESULTS Times in seconds 140 120 116 100 80 64 60 40 20 1 2 10*10 20*20 Job-shop 6 30*30 40*40 50*50 60*60 Power(Job-shop) Required time (Algorithm Ordinal-SCT) to schedule different job-shops: 10 ≤ n = m ≤ 60 16
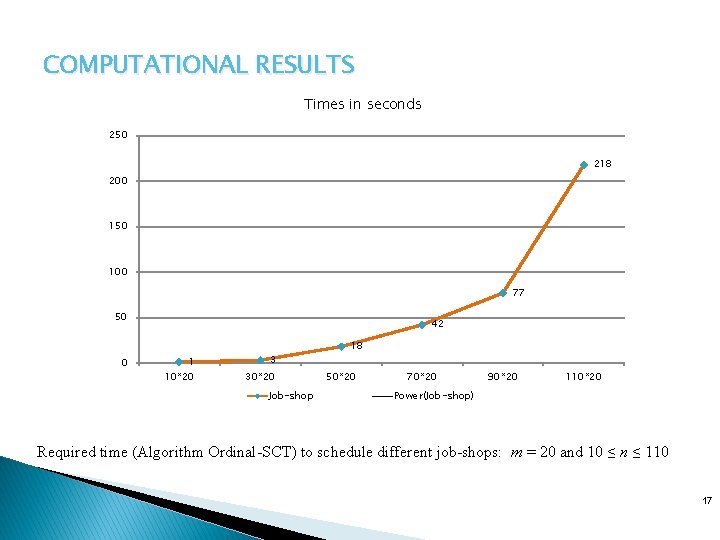
COMPUTATIONAL RESULTS Times in seconds 250 218 200 150 100 77 50 0 42 1 10*20 3 30*20 Job-shop 18 50*20 70*20 90*20 110*20 Power(Job-shop) Required time (Algorithm Ordinal-SCT) to schedule different job-shops: m = 20 and 10 ≤ n ≤ 110 17
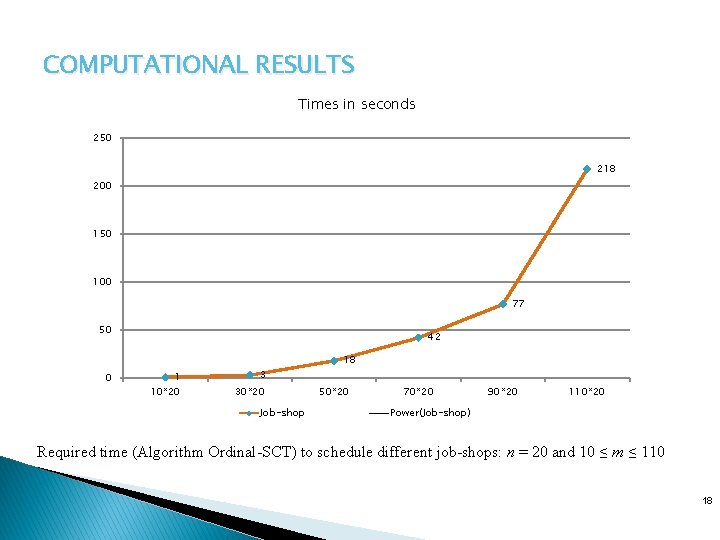
COMPUTATIONAL RESULTS Times in seconds 250 218 200 150 100 77 50 0 42 1 10*20 3 30*20 Job-shop 18 50*20 70*20 90*20 110*20 Power(Job-shop) Required time (Algorithm Ordinal-SCT) to schedule different job-shops: n = 20 and 10 ≤ m ≤ 110 18

COMPUTATIONAL RESULTS Ranking for ∑Ti ----------- 1. Ordinal-SCT 2. Ordinal-SRT 3. Min-PTRT 4. Min-PTCT Intel Core 2 Due CPU, 2. 00 GHz, Ram 2 GB, Windows 7 Ultimate, Borland Delphi programming language. Best constructive algorithm for the train scheduling problem among the tested ones is the Ordinal-SCT (Shortest Completion Time) algorithm. 5. Max-PTCT 6. Max-PTRT 7. Ordinal-SDD 8. Min-PTDD 9. Max-PTDD 19
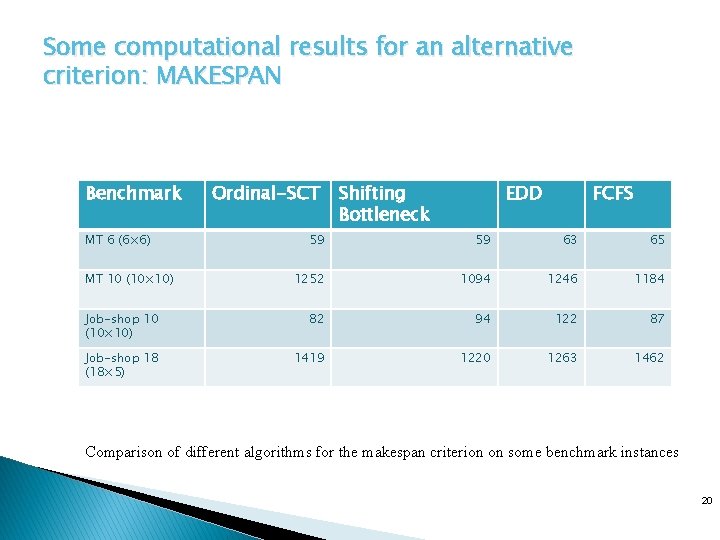
Some computational results for an alternative criterion: MAKESPAN Benchmark MT 6 (6× 6) Ordinal-SCT Shifting Bottleneck EDD FCFS 59 59 63 65 1252 1094 1246 1184 Job-shop 10 (10× 10) 82 94 122 87 Job-shop 18 (18× 5) 1419 1220 1263 1462 MT 10 (10× 10) Comparison of different algorithms for the makespan criterion on some benchmark instances 20

Thanks Heuristic Algorithms for a Job-Shop Problem with Minimizing Total Job Tardiness Yuri N. Sotskov 1, Omid Gholami 2, Frank Werner 3 1. United Institute of Informatics Problems, Minsk, Belarus, e-mail: sotskov@newman. bas-net. by 2. Islamic Azad university - Mahmudabad Branch, Mahmudabad, Iran, e-mail: gholami@iaumah. ac. ir 3. Faculty of Mathematics, Otto-von-Guericke-University, Magdeburg, Germany , e-mail: frank. werner@ovgu. de 21
- Slides: 21