Heteroscedasticity Jennifer Lehman Hossein Salehi Jacob Tenney Heteroscedasticity

Heteroscedasticity Jennifer Lehman Hossein Salehi Jacob Tenney

Heteroscedasticity Presentation Agenda � Story � Definition � Detection � Consequences � Solutions

This is Our Story �In this presentation, we will use an example from Personal Financial Planning. �Two variables: Annuities (Y) and Accumulated Wealth (X)
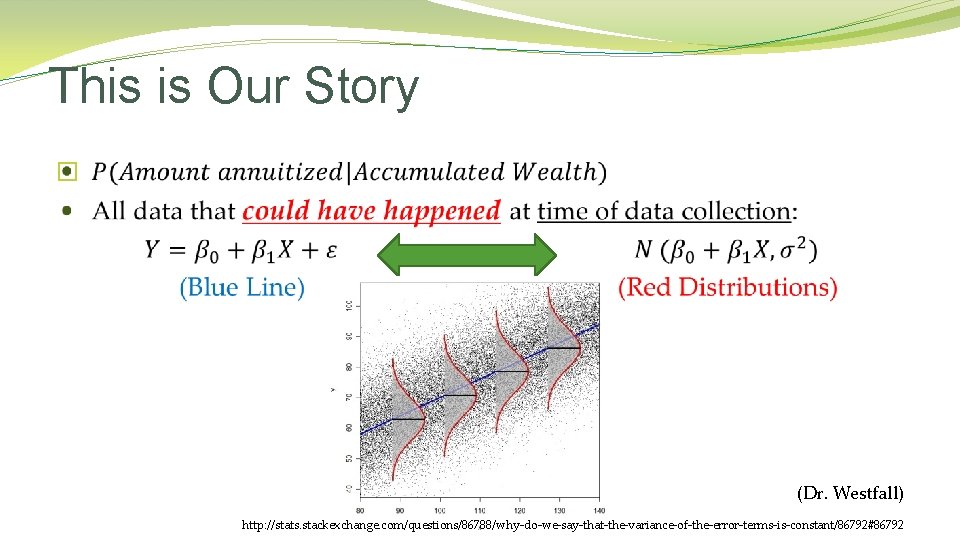
This is Our Story � (Dr. Westfall) http: //stats. stackexchange. com/questions/86788/why-do-we-say-that-the-variance-of-the-error-terms-is-constant/86792#86792

This is Our Story �

Definition Assumptions in Linear Regression Models The data generating process has: 1. Correct Functional Specification (Linearity) 2. Normality 3. Uncorrelated Error Terms (Conditional Independence) 4. Constant Variance (Homoscedasticity) (Dr. Westfall)
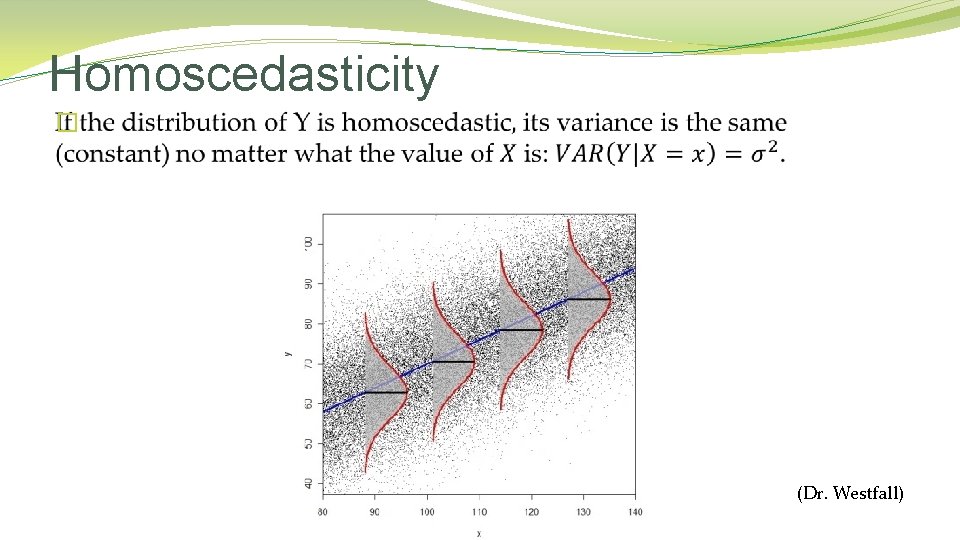
Homoscedasticity � (Dr. Westfall)
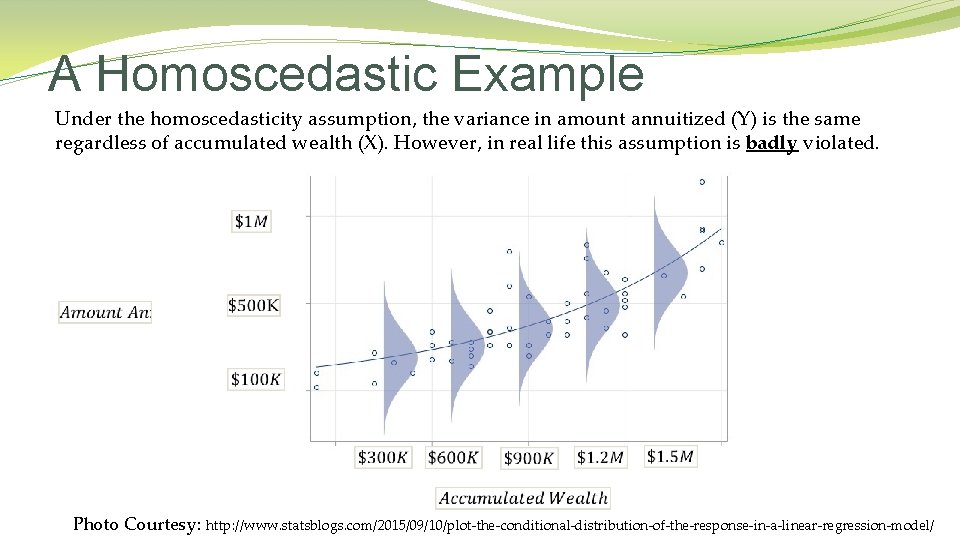
A Homoscedastic Example Under the homoscedasticity assumption, the variance in amount annuitized (Y) is the same regardless of accumulated wealth (X). However, in real life this assumption is badly violated. Photo Courtesy: http: //www. statsblogs. com/2015/09/10/plot-the-conditional-distribution-of-the-response-in-a-linear-regression-model/
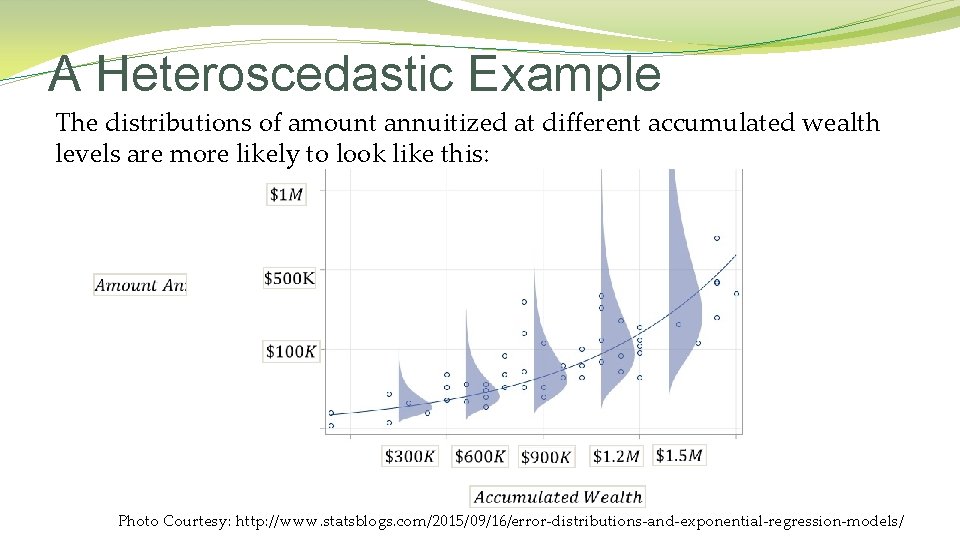
A Heteroscedastic Example The distributions of amount annuitized at different accumulated wealth levels are more likely to look like this: Photo Courtesy: http: //www. statsblogs. com/2015/09/16/error-distributions-and-exponential-regression-models/
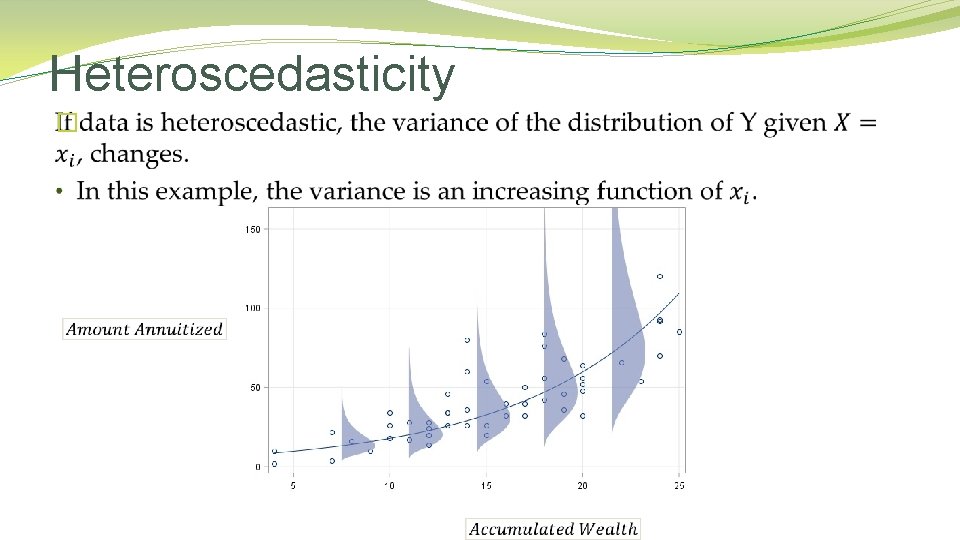
Heteroscedasticity �

Covariance Matrix Comparison � Homoscedasticity Heteroscedasticity

Detection �Plots �Use scatterplot to show the absolute residuals In our “amount annuitized” simulation, heteroscedasticity is evident from the data. However, this is not always the case.

Detection �

Detection CONCERNS BENEFITS TESTS GRAPHS • Transparency • Objective measure of what is explainable • “Practical Importance” is easily determined by chance alone • Larger sample sizes point us closer to the best • Sometimes required by journals answer when well-chosen graphs are used • All assumptions are violated, but the • Interpretation requires practice, judgment and question is how badly. statistical knowledge • Assumptions are null hypotheses, which • Generating good graphs requires skill and cannot be proven true. practice • Sample size: 1. Small sample: Low power, likely to fail to reject the null. 2. Large sample: Everything is significant • Tests are not perfectly objective. (Dr. Westfall, Feb. 2 reading material)

The Consequences of Heteroscedasticity 1. Wrong Standard Error: Heteroscedasticity causes the OLS estimates of the SE to be biased, leading to unreliable hypothesis testing. The variance formula tends to underestimate the true variance of the OLS estimate. 2. Inefficient OLS Estimate: Heteroscedasticity typically causes OLS to no longer be the minimum variance estimator (of all the linear unbiased estimators) (Lung-fei Lee, Ohio State University, Lectures 2001) (Walter Sosa-Escudero, 2009) (Blunch, 2011)

Ordinary Least Squares � (Paul Johnson, Oct. 2005)

Ordinary Least Squares �

The Consequences of Heteroscedasticity in Examples �
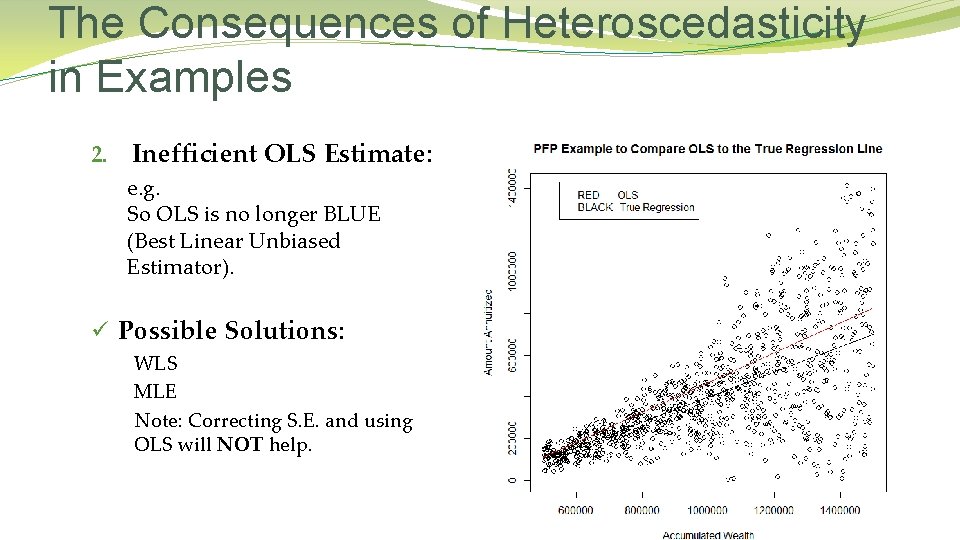
The Consequences of Heteroscedasticity in Examples 2. Inefficient OLS Estimate: e. g. So OLS is no longer BLUE (Best Linear Unbiased Estimator). ü Possible Solutions: WLS MLE Note: Correcting S. E. and using OLS will NOT help.

Solutions § Transformations § Weighted Least Squares § OLS with corrected standard errors § MLE

Solutions § Transformations § Weighted Least Squares § OLS with corrected standard errors § MLE
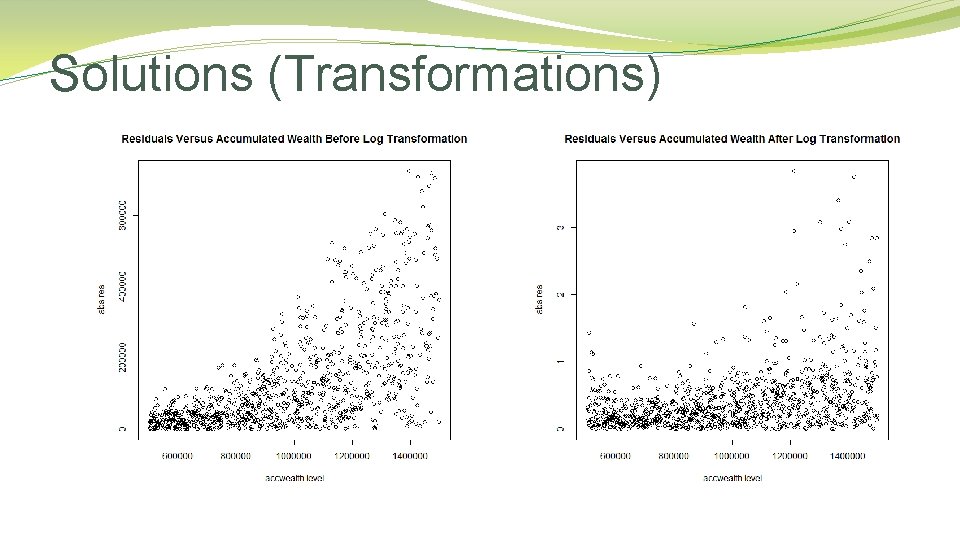
Solutions (Transformations)

Concerns with Transformations § Journals may not like it § Harder to interpret § It might not work, so we need to go back to the other solutions.

Solutions § Transformations § Weighted Least Squares § OLS with corrected standard errors § MLE

Covariance Matrix Comparison § Recall from what we discussed earlier, Homoscedasticity Heteroscedasticity

Comparing OLS and WLS OLS WLS Variance Function Sum of Squared Residuals Beta Estimates (Paul Johnson, Oct. 2005) (Ingo Ruczinski, Chapter 5)

Comparing OLS & WLS � (Maria L. Durban Reguera, UC 3 M reading material)
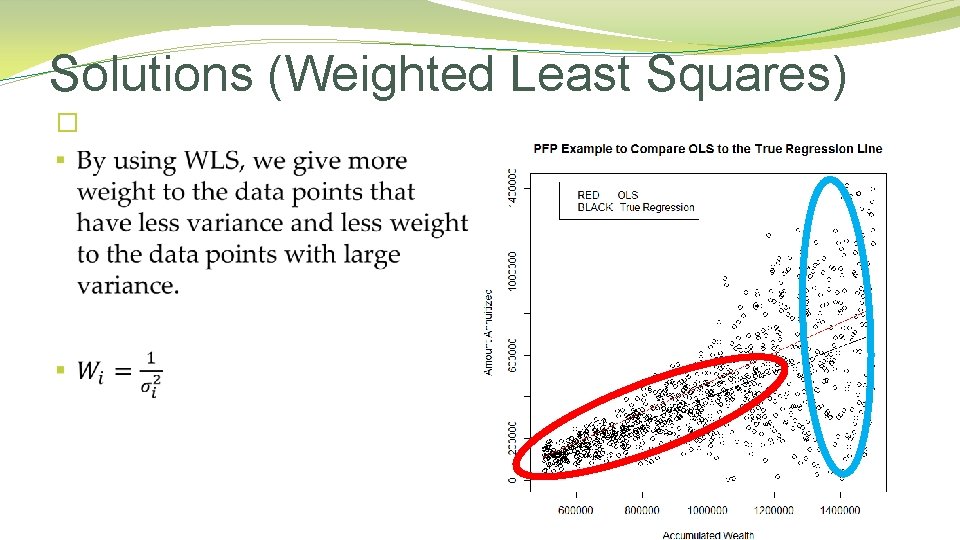
Solutions (Weighted Least Squares) �
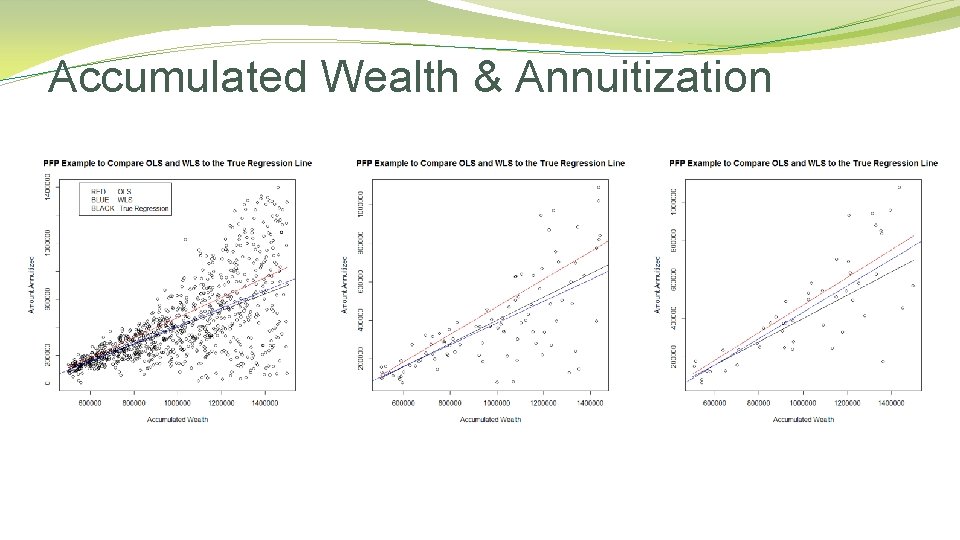
Accumulated Wealth & Annuitization
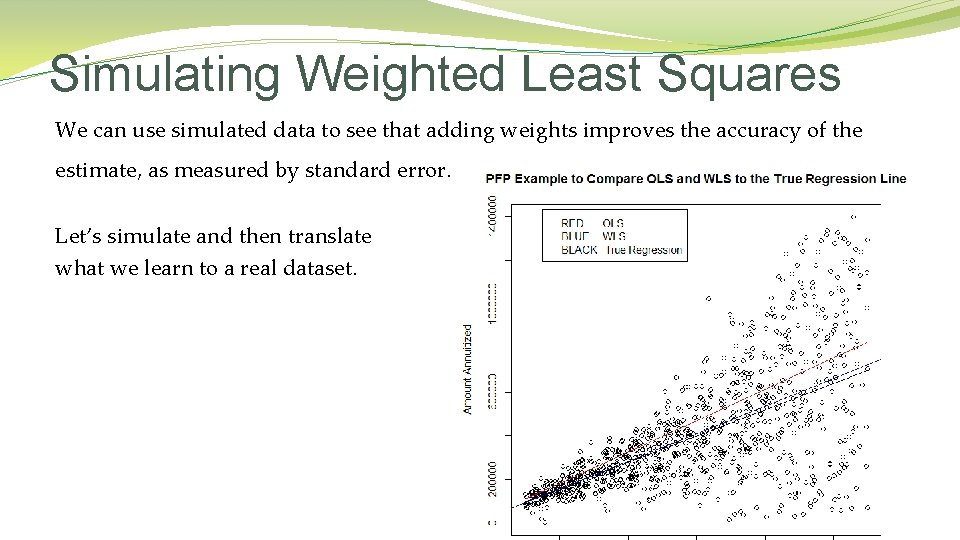
Simulating Weighted Least Squares We can use simulated data to see that adding weights improves the accuracy of the estimate, as measured by standard error. Let’s simulate and then translate what we learn to a real dataset.

Benefits of WLS § With the right weight function, the estimates are efficient and MLE.

Problems with WLS § BUT … How do we determine the weights when we do not know the variances? (Cosma Shalizi, Oct. 2009)

Problems with WLS § What if … The Oracle may be out or too creepy to visit. (Cosma Shalizi, Oct. 2009)

Weighted Least Squares �

Solutions § Transformations § Weighted Least Squares § OLS with corrected standard errors § MLE

Ordinary Least Squares � (Paul Johnson, Oct. 2005)

OLS With Corrected Standard Errors (Consistent Covariance Matrix) �

Other Solutions �

Wrapping Up � Story � Definition � Detection � Consequences � Solutions

Reference Page �Dr. Westfall �Niels-Hugo Blunch, 2011, Using Econometrics A Practical Guide, Pearson. �Walter Sosa-Escudero, 2009, Heteroscedasticity and WLS �http: //halweb. uc 3 m. es/esp/Personal/personas/durban/esp/web/notes/gls. pdf �Ingo Ruczinski webpage: http: //www. biostat. jhsph. edu/~iruczins/teaching/jf/ch 5. pdf �Paul Johnson, Oct. 2005. �Maria L. Durban Reguera, reading material: http: //halweb. uc 3 m. es/esp/Personal/personas/durban/esp/web/notes/gls. pdf �Cosma Shalizi, Oct. 2009, Extending Linear Regression: Weighted Least Squares, Heteroskedasticity, Local Polynomial Regression �Westfall and Henning , 2013, Understanding Advanced Statistical Methods �Drew Dimmery, April 2012, Robust SEs in R, http: //www. drewdimmery. com/robustses-in-r/

Photo Credit Page � Slide 4: http: //stats. stackexchange. com/questions/86788/why-do-we-say-that-the-variance-ofthe-error-terms-is-constant/86792#86792 � Slide 5: http: //www. statsblogs. com/2015/09/10/plot-the-conditional-distribution-of-theresponse-in-a-linear-regression-model/ � Slide 6: http: //www. statsblogs. com/2015/09/16/error-distributions-and-exponential-regression -models/ � Slides 33 and 34: Cosma Shalizi, Oct. 2009.

Thank you & Enjoy Your Spring Break!
- Slides: 42