Herramientas Computacionales Trabajo con vectores en MATLAB Patricio

Herramientas Computacionales Trabajo con vectores en MATLAB Patricio Poblete Maíra Marques Enero 2015

MATLAB Los vectores vienen en dos sabores Vector fila (separados por espacios o comas) >> x = [10 20 30] x = 10 20 30 Vector columna (separados por punto y coma o cambios de línea) >> y = [3; 2; 1] y = 3 2 1 3

MATLAB Los vectores del mismo tipo y tamaño se pueden sumar y restar. >> x=[5, -3, 8] x = 5 -3 8 >> y=[1, 7, -6] y = 1 7 -6 >> x+y ans = 6 4 2 4

MATLAB Una operación matemáticamente importante es el producto interno entre un vector fila y un vector columna: x = 30 10 20 >> x * y ans = 100 y = 3 2 1 % 10*3 +20*2 + 30*1 5

MATLAB La operación de trasposición x’ transforma un vector x de fila a columna y viceversa. Norma euclidiana de un vector x: >> sqrt( x * x' ) ans = 37. 417 6

MATLAB En MATLAB, una operación mucho más usada es el producto componente a componente (. *). Se aplica a dos vectores del mismo tipo y tamaño, y el resultado es el vector de los productos de las componentes respectivas. >> x = [5 3 2 x = 5 3 >> y = [2 1 4 y = 2 1 >> z = x. * y z = 10 3 6] 2 3] 4 6 3 8 18 7

MATLAB Graficar la función x*sin(x) para x en [0, 6π] >> x = linspace(0, 6*pi); >> y = x. * sin(x); >> plot(x, y) >> grid 8

MATLAB División componente a componente (. /) Ejemplo: Calcular 1+1/2+1/3+1/4+1/5 >> unos = ones(1, 5) unos = 1 1 1 >> n = 1: 5 n = 1 2 3 4 5 >> fracciones = unos. / n fracciones = 1. 00000 0. 50000 0. 33333 0. 25000 0. 20000 >> sum(fracciones) ans = 2. 2833 >> sum( 1. /(1: 5) ) ans = 2. 2833 9

MATLAB Elevación a potencia (. ^) Ejemplo: Cálculo de la norma euclidiana >> x = [10 20 30] x = 10 20 30 >> sqrt(sum( x. ^2 )) ans = 37. 417 10

MATLAB Corregir un test de alternativas Respuestas del 1 al 5, un cero indica respuesta omitida. El operador == compara por igualdad, retorna 0 ó 1. >> plantilla = [4 2 5 1 4 3 2 5 1 3 2] plantilla = 4 2 5 1 4 3 2 >> respuestas = [4 0 5 2 4 0 2 3 1 0 1] respuestas = 4 0 5 2 4 0 2 >> sum( plantilla==respuestas ) ans = 5 5 1 3 3 1 2 0 1 11

MATLAB Ejercicio: Repetir lo anterior, descontando ¼ por cada respuesta incorrecta (exceptuando las omitidas) 12

MATLAB >> sum(plantilla==respuestas) – sum(plantilla~=respuestas & respuestas~=0)/4 ans = 4. 2500 >> correctas = sum(plantilla==respuestas) correctas = 5 >> correctas – (length(plantilla)-correctassum(respuestas==0))/4 ans = 4. 2500 13

MATLAB Tiro al blanco 14

MATLAB Lanzar dardos al azar sobre un círculo inscrito en un cuadrado de 1 x 1, calculando la fracción de ellos que caen dentro del círculo 15

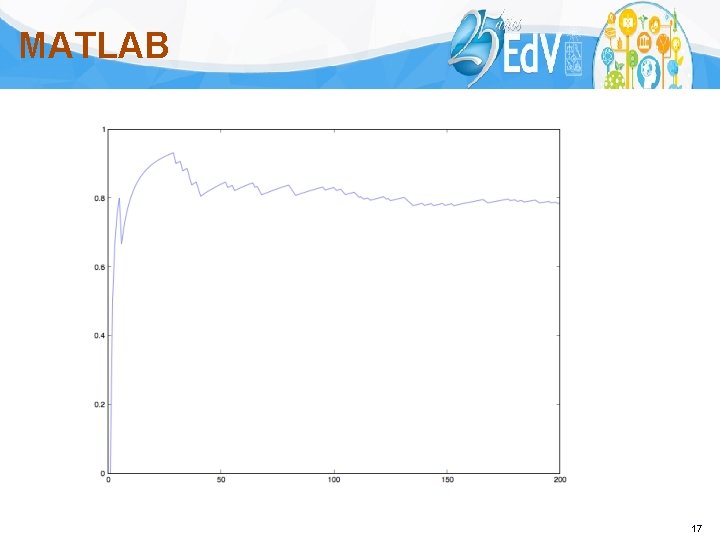
MATLAB >> >> x=rand(1, 200); y=rand(1, 200); in=(x-1/2). ^2+(y-1/2). ^2<=1/4; acum=cumsum(in); n=1: 200; fraccion=acum. /n; plot(n, fraccion) 16

MATLAB 17

MATLAB Ejercicio: Realizar el experimento con más lanzamientos y ver si se mantiene la tendencia. ¿A qué número converge? 18

MATLAB Triángulo de Pascal Son los coeficientes de la expansión de (x+y)n para n=0, 1, 2, … 1 1 1 2 3 4 1 3 6 1 4 1 19

MATLAB De la segunda fila en adelante, cada número es la suma de los dos que están inmediantamente encima de él (suponiendo que las filas se extienden con ceros hacia los lados) 1 1 1 2 3 4 1 3 6 1 4 1 20

MATLAB Ejercicio: Dado un vector a de largo 10 que contiene una fila del triángulo de Pascal (con un cero al inicio y rellena de ceros al final), calcular la siguiente fila y dejarla en el mismo vector a. El vector inicial sería: >> a=zeros(1, 10); a(2)=1 a = 0 1 0 0 0 0 21

MATLAB 22

MATLAB Solución “clásica” >> for i=2: 10 b(i)=a(i-1)+a(i); end >> a=b Solución “estilo MATLAB” >> a(2: 10)=a(1: 9)+a(2: 10) 23

MATLAB 24