Herons method for finding the area of a

Heron, also Hero ( c 1 st century AD) Greek mathematician and inventor. He

Find the area of a triangle with side lengths 13 cm, 14 cm and

Find the area of a triangle with side lengths 8 cm, 10 cm and

The method we used to calculate the area of a triangle given its 3

We found earlier that: • a triangle with sides 13 cm, 14 cm and

The area of a right angled triangle whose. Triangles 3 side lengths Such triangles

Such triangles are known as Heron’s Triangles They have integer side lengths and integer

Another example of a pair of “Pythagorean triple” triangles added and subtracted to create

Slides: 26

Download presentation

Heron’s method for finding the area of a triangle © T Madas

Heron, also Hero ( c 1 st century AD) Greek mathematician and inventor. He devised many machines such as a fire engine, a water organ, several coin operated devices and the earliest known form of a steam engine, shown opposite. He proved that the angle of incidence in optics is equal to the angle of reflection. In Mathematics he is credited with a formula which gives the area of a triangle if its three sides are known. © T Madas

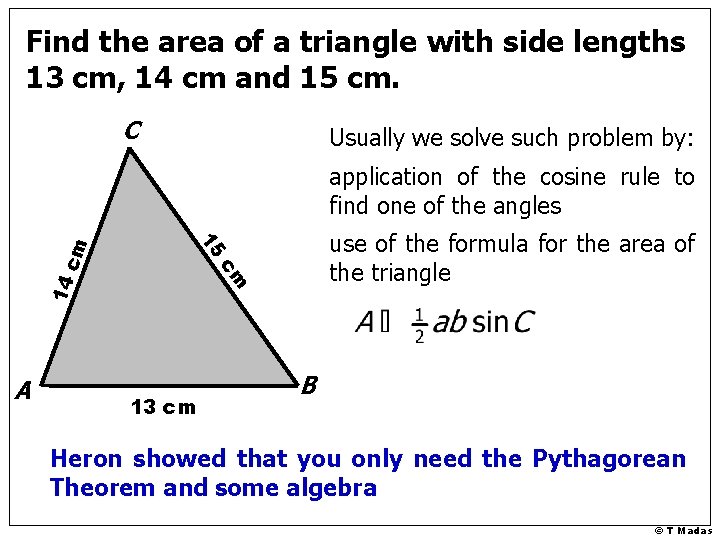
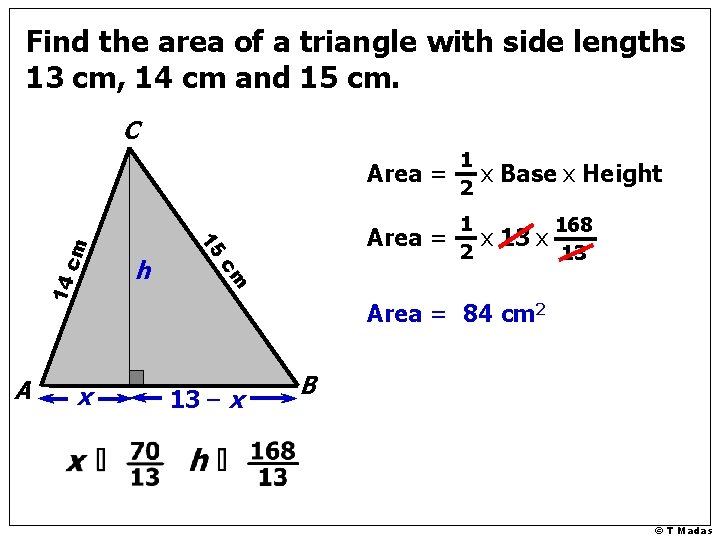
Find the area of a triangle with side lengths 13 cm, 14 cm and 15 cm. C Usually we solve such problem by: 14 cm A use of the formula for the area of the triangle 15 cm application of the cosine rule to find one of the angles 13 cm B Heron showed that you only need the Pythagorean Theorem and some algebra © T Madas

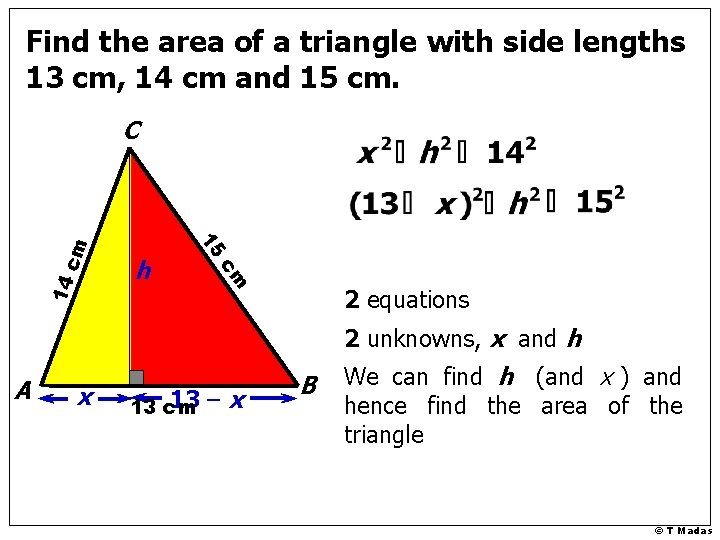
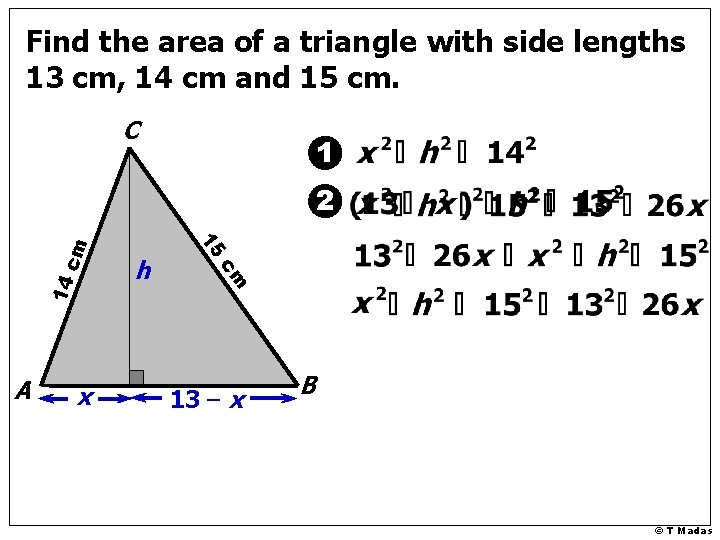
Find the area of a triangle with side lengths 13 cm, 14 cm and 15 cm. 14 cm h 15 cm C 2 equations 2 unknowns, x and h A x 13 13 cm –x B We can find h (and x ) and hence find the area of the triangle © T Madas

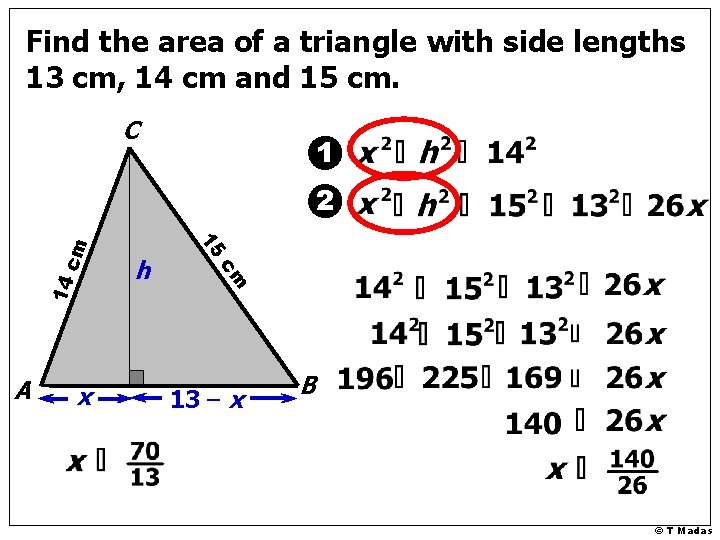
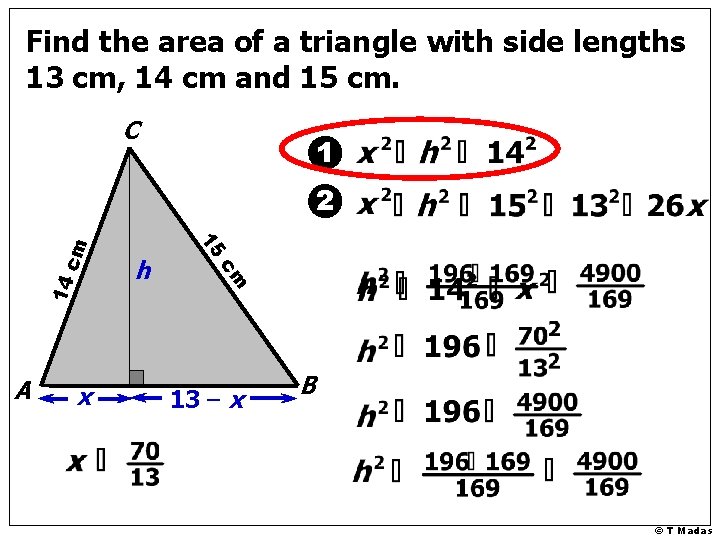
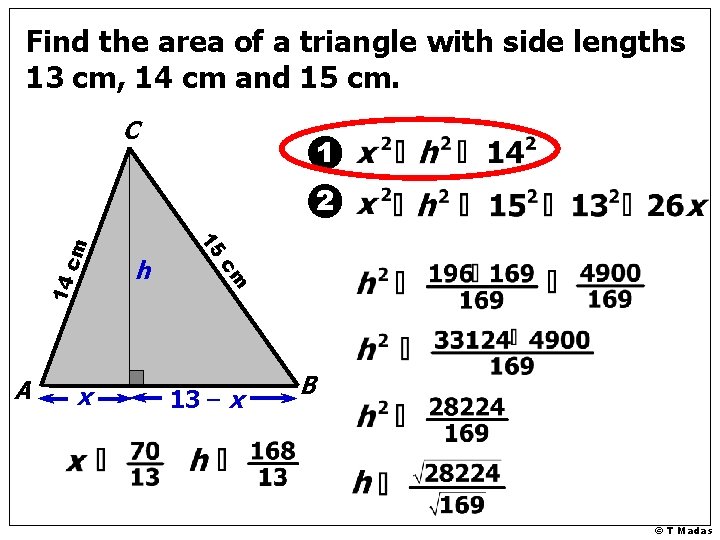
Find the area of a triangle with side lengths 13 cm, 14 cm and 15 cm. C 1 14 x cm A h 15 cm 2 13 – x B © T Madas

Find the area of a triangle with side lengths 13 cm, 14 cm and 15 cm. 14 x Area = 1 2 x Base x Height Area = 1 2 168 13 x cm A h 15 cm C Area = 84 cm 2 13 – x B © T Madas

Take notes on another example © T Madas

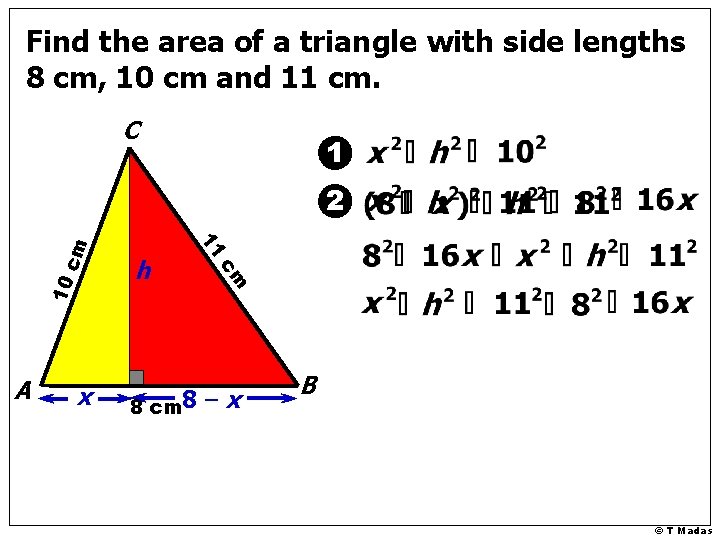
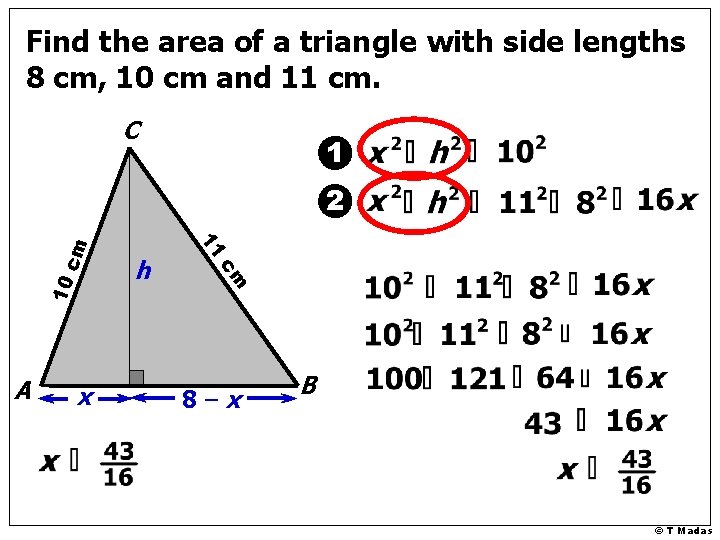
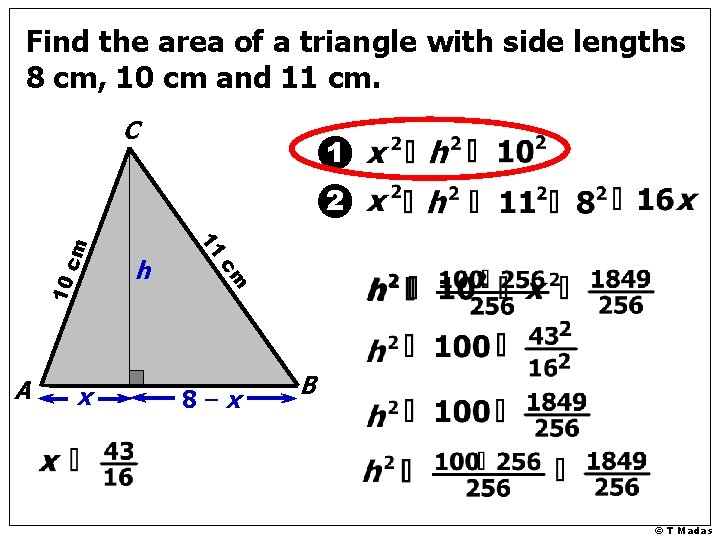
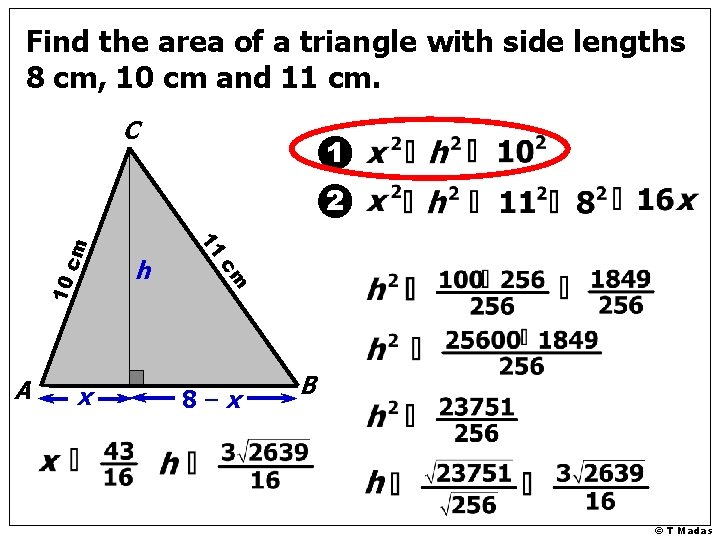
Find the area of a triangle with side lengths 8 cm, 10 cm and 11 cm. C 1 10 x cm A h 11 cm 2 8 cm 8 – x B © T Madas

Find the area of a triangle with side lengths 8 cm, 10 cm and 11 cm. C 1 10 x cm A h 11 cm 2 8–x B © T Madas

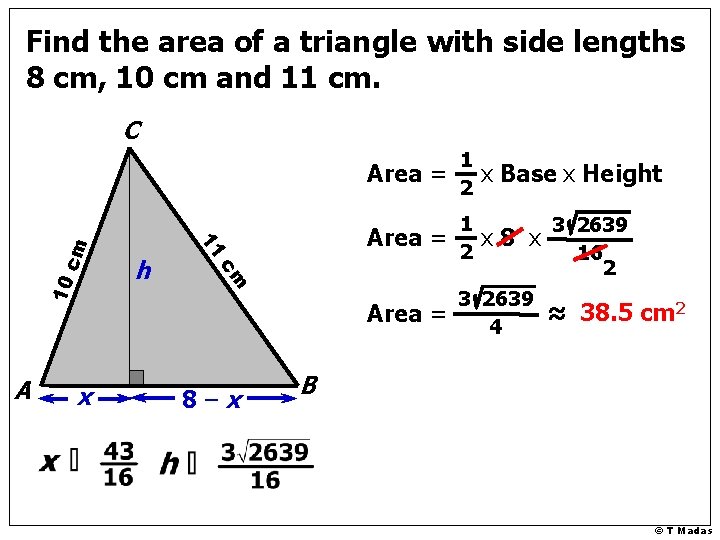
Find the area of a triangle with side lengths 8 cm, 10 cm and 11 cm. 10 x Area = 1 2 Area = 3 2639 4 cm A h 11 cm C 8–x x Base x Height x 8 x 3 2639 16 2 ≈ 38. 5 cm 2 B © T Madas

The method we used to calculate the area of a triangle given its 3 sides, can be generalised to a triangle with sides a, b and c. We can obtain a general result known as Heron’s formula. It states that the area of triangle of side lengths a, b and c is given by: A = s (s – a ) (s – b ) (s – c ) where s = 1 (a 2 +b+c) [The algebra for deriving the general case, is a bit more involved and has been omitted] © T Madas

We found earlier that: • a triangle with sides 13 cm, 14 cm and 15 cm has area 84 cm 2 • a triangle with sides 8 cm, 10 cm and 11 cm has area ≈ 38. 53 cm 2 Using Heron’s formula: © T Madas

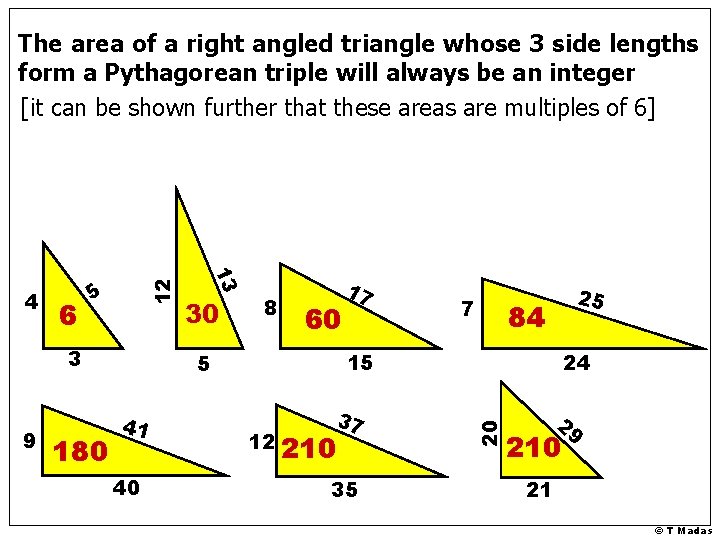
3 9 180 30 8 60 40 7 25 84 15 5 41 17 37 12 210 35 24 20 6 5 13 4 12 The area of a right angled triangle whose 3 side lengths form a Pythagorean triple will always be an integer [it can be shown further that these areas are multiples of 6] 29 210 21 © T Madas

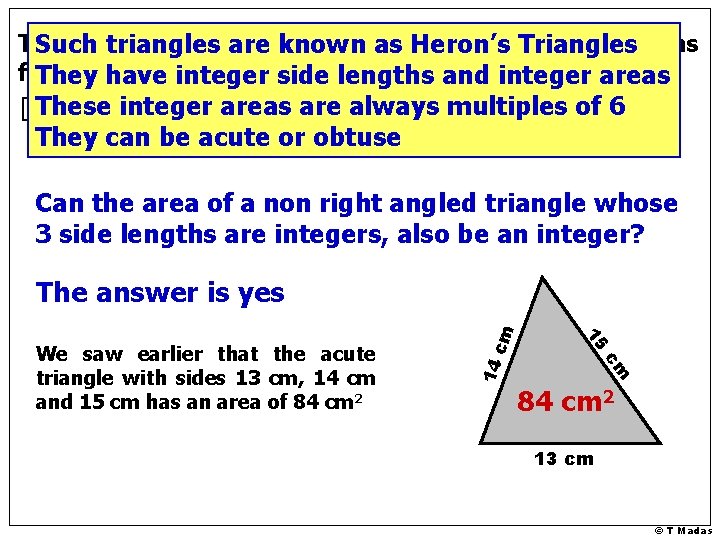
The area of a right angled triangle whose. Triangles 3 side lengths Such triangles are known as Heron’s form a Pythagorean always beinteger an integer They have integertriple side will lengths and areasthat arethese always of of 6 6] [it. These can beinteger shown further areasmultiples are multiples They can be acute or obtuse Can the area of a non right angled triangle whose 3 side lengths are integers, also be an integer? cm 14 15 We saw earlier that the acute triangle with sides 13 cm, 14 cm and 15 cm has an area of 84 cm 2 cm The answer is yes 84 cm 2 13 cm © T Madas

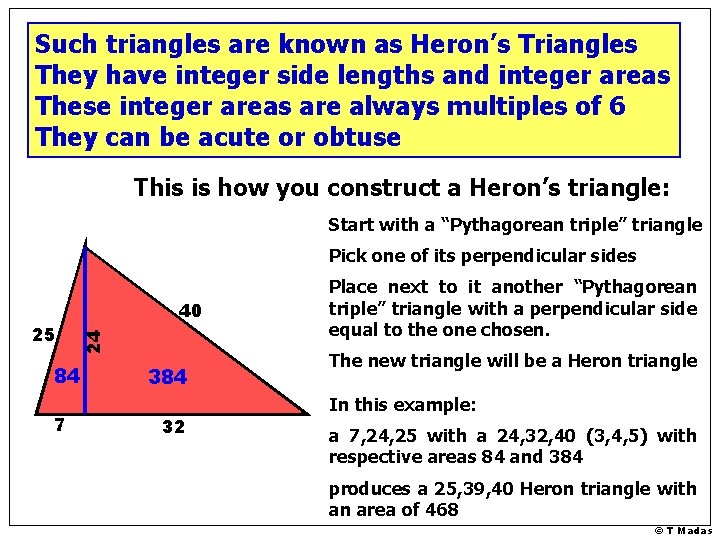
Such triangles are known as Heron’s Triangles They have integer side lengths and integer areas These integer areas are always multiples of 6 They can be acute or obtuse This is how you construct a Heron’s triangle: Start with a “Pythagorean triple” triangle Pick one of its perpendicular sides 24 25 40 84 7 384 32 Place next to it another “Pythagorean triple” triangle with a perpendicular side equal to the one chosen. The new triangle will be a Heron triangle In this example: a 7, 24, 25 with a 24, 32, 40 (3, 4, 5) with respective areas 84 and 384 produces a 25, 39, 40 Heron triangle with an area of 468 © T Madas

Such triangles are known as Heron’s Triangles They have integer side lengths and integer areas These integer areas are always multiples of 6 They can be acute or obtuse We can always produce a second Heron triangle using the same 2 Pythagorean triangles: 24 25 25 40 subtracting: a 7, 24, 25 from a 24, 32, 40 (3, 4, 5) with respective areas 84 and 384 produces a 25, 32, 40 Heron triangle with an area of 300 7 7 32 © T Madas

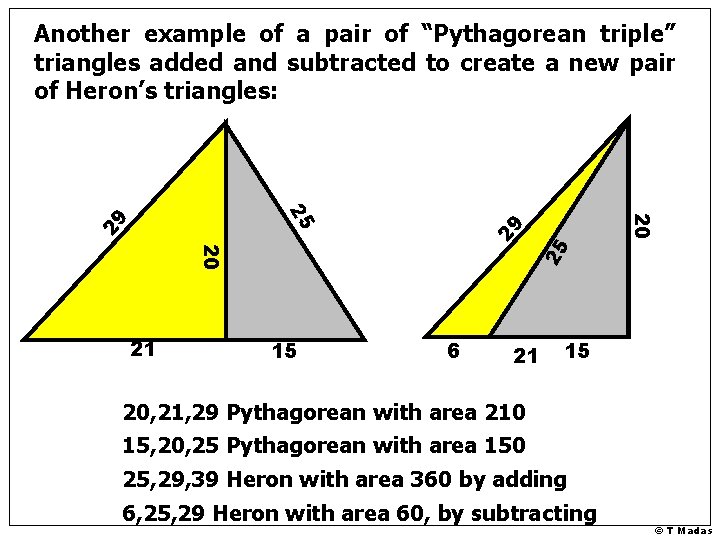
Another example of a pair of “Pythagorean triple” triangles added and subtracted to create a new pair of Heron’s triangles: 29 29 20 25 25 20 21 15 6 21 15 20, 21, 29 Pythagorean with area 210 15, 20, 25 Pythagorean with area 150 25, 29, 39 Heron with area 360 by adding 6, 25, 29 Heron with area 60, by subtracting © T Madas