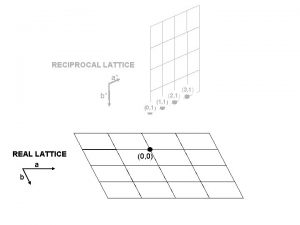
here Reciprocal Lattice Ewald Sphere Construction q Reciprocal















- Slides: 45

here) Reciprocal Lattice & Ewald Sphere Construction q Reciprocal lattice. Reciprocal Crystal. Part of MATERIALS SCIENCE & A Learner’s Guide ENGINEERING AN INTRODUCTORY E-BOOK Anandh Subramaniam & Kantesh Balani Materials Science and Engineering (MSE) Indian Institute of Technology, Kanpur- 208016 Email: anandh@iitk. ac. in, URL: home. iitk. ac. in/~anandh http: //home. iitk. ac. in/~anandh/E-book. htm q Structure factor calculations. q Ewald sphere construction. q Diffraction patterns. Diffraction Patterns q The concepts of reciprocal lattice, structure factor calculations (and sometimes Ewald sphere construction) often ‘strike terror’ in the hearts of students. q However, these concepts are not too difficult if the fundamentals are understood in 1 D and then extended to 3 D. Read these slides in parallel

Reciprocal Lattice and Reciprocal Crystals Why study reciprocal lattices? Often the concepts related to reciprocal lattice strikes terror in the minds of students. As we shall see this is not too difficult if concepts are first understood in 1 D. q A crystal resides in real space. The diffraction pattern# resides in Reciprocal Space. q In a diffraction experiment (e. g. powder diffraction using X-rays, selected area diffraction in a TEM), a part of this reciprocal space is usually sampled. q The diffraction pattern from a crystal (in Fraunhofer diffraction geometry), consists of a periodic array of spots (sharp peaks of intensity) [1]. (Click here to know the conditions under which this is satisfied). q From the real lattice the reciprocal lattice can be geometrically constructed. The properties of the reciprocal lattice are ‘inverse’ of the real lattice → planes ‘far away’ in the real crystal are closer to the origin in the reciprocal lattice. q As a real crystal can be thought of as decoration of a lattice with motif; a reciprocal crystal can be visualized as a Reciprocal Lattice decorated with a motif* of Intensities. Reciprocal Crystal = Reciprocal Lattice + Intensities as Motif* q The reciprocal of the ‘reciprocal lattice’ is nothing but the real lattice! q Planes in real lattice become points in reciprocal lattice and vice-versa. I. e. the information needed is the geometry of the lattice. * Clearly, this is not the “crystal motif”- but a motif consisting of “Intensities”. # The complete diffraction pattern (not the one observed in an experiment). The one observed in an experiment is a subset of this, which can be found by the Ewald Sphere construction. [1] The diffraction pattern can be obtained by Fourier transform of the crystal in real space.

A motivation for constructing reciprocal lattices q In diffraction patterns (Fraunhofer geometry & under conditions listed here: (Click here to know the conditions under which this is satisfied). ) (e. g. SAD), planes are mapped as spots (ideally points). This as you will remember is the Bragg’s viewpoint of diffraction. Hence, we would like to have a construction which maps planes in a real crystal as points. q Apart from the use in ‘diffraction studies’ we will see that it makes sense to use reciprocal lattice when we are dealing with planes. q The crystal ‘resides’ in Real Space, while the diffraction pattern ‘lives’ in Reciprocal Space. q As the index of the plane increases → the interplanar spacing decreases → and ‘planes start to crowd’ in the real lattice (refer figure). Hence, it is a ‘nice idea’ to work in reciprocal space (i. e. work with the reciprocal lattice), especially when dealing with planes. As index of the plane increases, the interplanar spacing decreases In the figure the axes and origin are chosen locally

formal definition in 3 D Let us start with a one dimensional lattice and construct the reciprocal lattice Real Lattice Natura l origin of the r eciproc al lattic e O Reciprocal Lattice § The periodic array of points with lattice parameter ‘a’ is transformed to a reciprocal lattice with periodicity of ‘ 1/a’. § The reciprocal lattice point at a distance of 1/a from the origin (O), represents the whole set of points (at a, 2 a, 3 a, 4 a, …. ) in real space. § The reciprocal lattice point at ‘ 2/a’ comes from a set of points with fractional lattice spacing a/2 (i. e. with periodicity of a/2). The lattice with periodicity of ‘a’ is a subset of this lattice with periodicity of a/2. (Refer next slide). § The reciprocal lattice has a natural origin (labelled ‘O’). As we shall see it is indexed ‘ 0’.

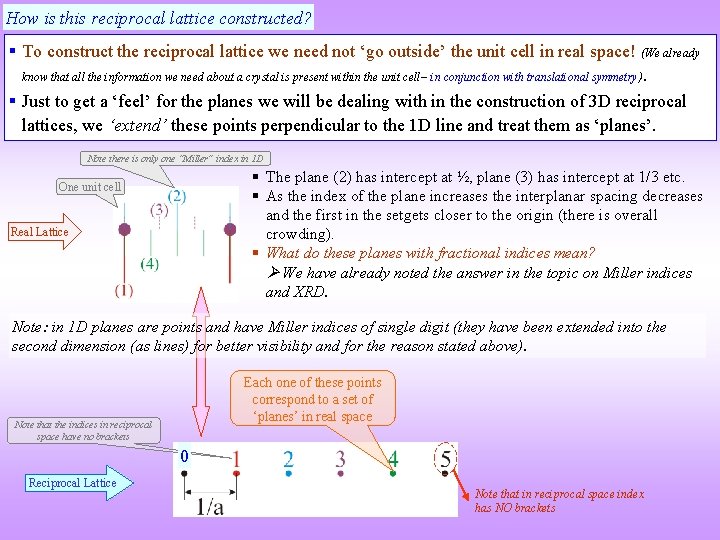
How is this reciprocal lattice constructed? § To construct the reciprocal lattice we need not ‘go outside’ the unit cell in real space! (We already know that all the information we need about a crystal is present within the unit cell– in conjunction with translational symmetry). § Just to get a ‘feel’ for the planes we will be dealing with in the construction of 3 D reciprocal lattices, we ‘extend’ these points perpendicular to the 1 D line and treat them as ‘planes’. Note there is only one “Miller” index in 1 D § The plane (2) has intercept at ½, plane (3) has intercept at 1/3 etc. § As the index of the plane increases the interplanar spacing decreases and the first in the setgets closer to the origin (there is overall crowding). § What do these planes with fractional indices mean? We have already noted the answer in the topic on Miller indices and XRD. One unit cell Real Lattice Note: in 1 D planes are points and have Miller indices of single digit (they have been extended into the second dimension (as lines) for better visibility and for the reason stated above). Each one of these points correspond to a set of ‘planes’ in real space Note that the indices in reciprocal space have no brackets 0 Reciprocal Lattice Note that in reciprocal space index has NO brackets

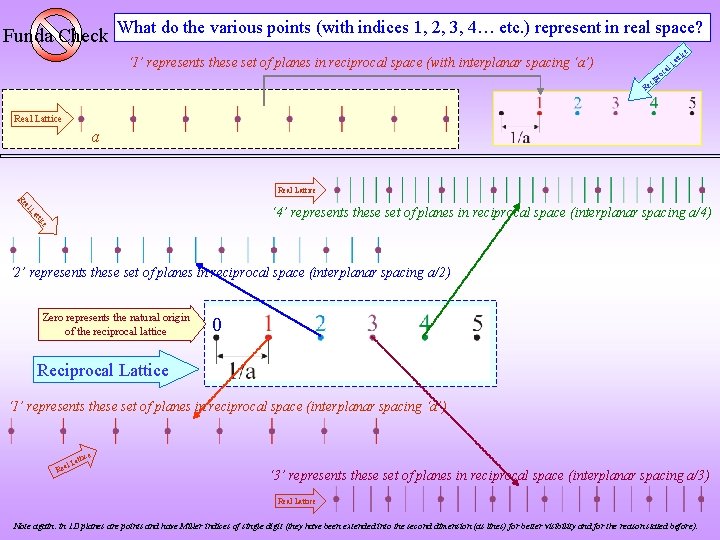
Funda Check What do the various points (with indices 1, 2, 3, 4… etc. ) represent in real space? ce tti ‘ 1’ represents these set of planes in reciprocal space (with interplanar spacing ‘a’) a l. L a cip c ro Re Real Lattice al Re ice tt La ‘ 4’ represents these set of planes in reciprocal space (interplanar spacing a/4) ‘ 2’ represents these set of planes in reciprocal space (interplanar spacing a/2) Zero represents the natural origin of the reciprocal lattice 0 Reciprocal Lattice ‘ 1’ represents these set of planes in reciprocal space (interplanar spacing ‘a’) l Rea Lat tice ‘ 3’ represents these set of planes in reciprocal space (interplanar spacing a/3) Real Lattice Note again: in 1 D planes are points and have Miller indices of single digit (they have been extended into the second dimension (as lines) for better visibility and for the reason stated before).

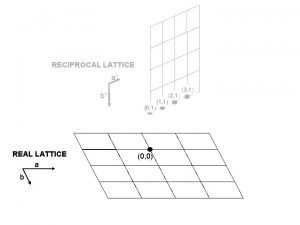
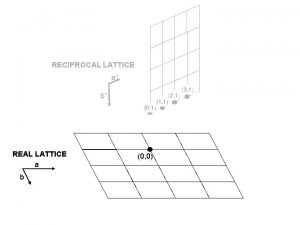
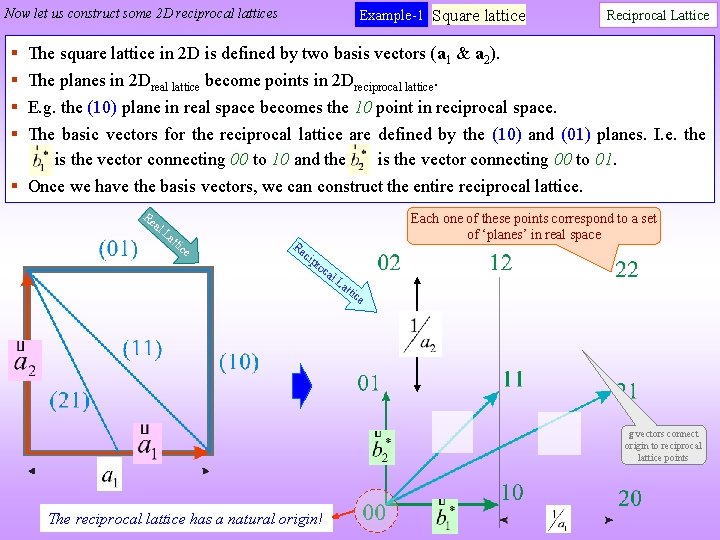
Now let us construct some 2 D reciprocal lattices § § Example-1 Square lattice Reciprocal Lattice The square lattice in 2 D is defined by two basis vectors (a 1 & a 2). The planes in 2 Dreal lattice become points in 2 Dreciprocal lattice. E. g. the (10) plane in real space becomes the 10 point in reciprocal space. The basic vectors for the reciprocal lattice are defined by the (10) and (01) planes. I. e. the is the vector connecting 00 to 10 and the is the vector connecting 00 to 01. § Once we have the basis vectors, we can construct the entire reciprocal lattice. Re al La tti c e Re Each one of these points correspond to a set of ‘planes’ in real space cip ro ca l. L att ice g vectors connect origin to reciprocal lattice points The reciprocal lattice has a natural origin!

§ If we overlay the real and reciprocal lattices then we can see that: 11 vector in reciprocal space is orthogonal to the (11) planes in real space. § I. e. planes in real space are orthogonal to the corresponding reciprocal lattice vector. The 11 vector in reciprocal space is : Any general vector in a 2 D reciprocal lattice is given by: This can be generalized to 3 D as: Note that the indices corresponding to the real spaces planes; i. e. h, k & l are retained as subscripts to the vector g in the reciprocal space. Overlay of real and reciprocal lattices Note that vectors in reciprocal space are perpendicular to planes in real space (as constructed!) But do not measure distances from the figure!

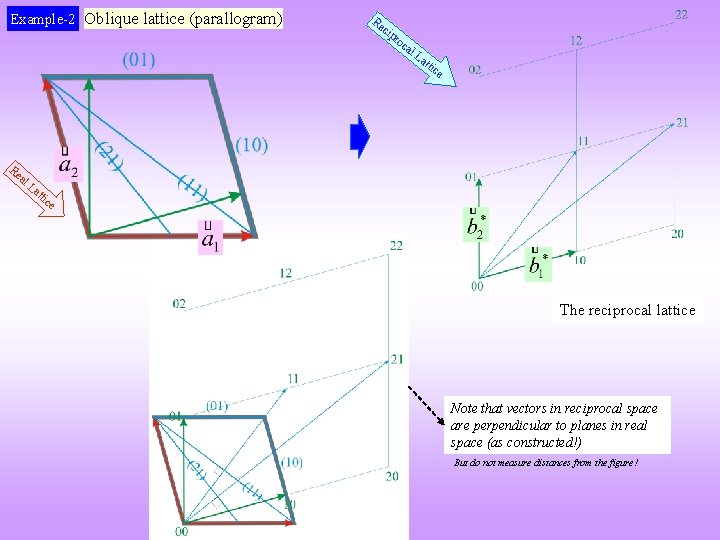
Example-2 Oblique lattice (parallogram) Re cip ro ca l. L att ice Re al La tt ice The reciprocal lattice Note that vectors in reciprocal space are perpendicular to planes in real space (as constructed!) But do not measure distances from the figure!

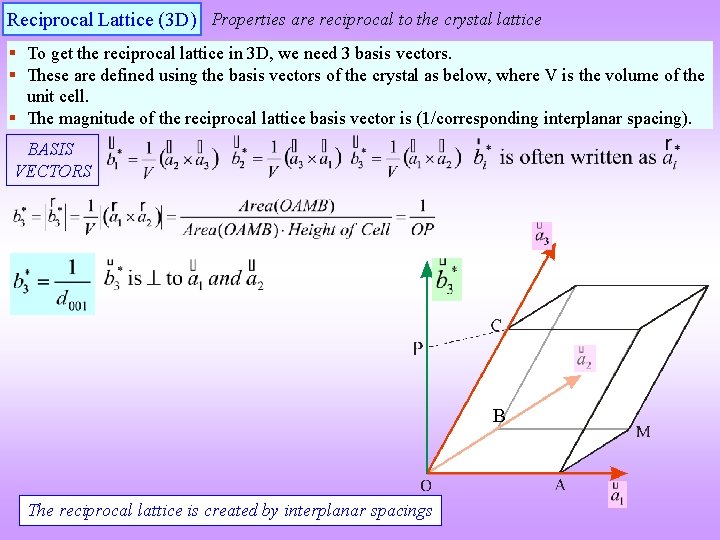
Reciprocal Lattice (3 D) Properties are reciprocal to the crystal lattice § To get the reciprocal lattice in 3 D, we need 3 basis vectors. § These are defined using the basis vectors of the crystal as below, where V is the volume of the unit cell. § The magnitude of the reciprocal lattice basis vector is (1/corresponding interplanar spacing). BASIS VECTORS B The reciprocal lattice is created by interplanar spacings

Some properties of the reciprocal lattice and its relation to the real lattice § A reciprocal lattice vector is to the corresponding real lattice plane § The length of a reciprocal lattice vector is the reciprocal of the spacing of the corresponding real lattice plane § Planes in the crystal become lattice points in the reciprocal lattice Note that this is an alternate geometrical construction of the real lattice. § Reciprocal lattice point represents the orientation and spacing of a set of planes. Notation for basis vectors Basis vectors in real space Basis vectors in reciprocal space (lattice) Basis vectors in reciprocal space (crystal) General vector in real space General vector in reciprocal space Lattice translation vectors (UC basis vectors) Reciprocal Crystal: basis vectors New notation of UC. “May be” identical to the basis vectors of the reciprocal lattice

Going from the reciprocal lattice to diffraction spots in an experiment q A Selected Area Diffraction (SAD) pattern in a TEM is similar to a section through the reciprocal lattice (or more precisely the reciprocal crystal, wherein each reciprocal lattice point has been decorated with a certain intensity). q The reciprocal crystal has all the information about the atomic positions and the atomic species (i. e. I have to look into both the positions of the points and the intensities decorating them). Revision+ q Reciprocal lattice* is the reciprocal of a primitive lattice and is purely geometrical does not deal with the intensities decorating the points. Physics comes in from the following: q For non-primitive cells ( lattices with additional points) and for crystals having motifs ( crystal = lattice + motif) the Reciprocal lattice points have to be weighed in with the corresponding scattering power (|Fhkl|2) (Where F is the structure factor). Some of the Reciprocal lattice points go missing (or may be scaled up or down in intensity). Making of Reciprocal Crystal: Reciprocal lattice decorated with a motif of scattering power (as intensities). q The Ewald sphere construction further can select those points (regions of reciprocal space), which can be observed in a diffraction experiment. q The intensity actually observed in an experiment depends on the ‘detector set-up’. * as considered here

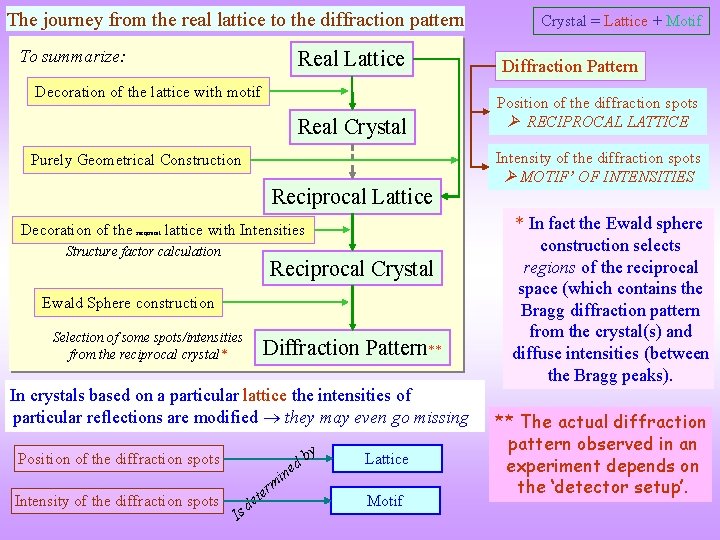
The journey from the real lattice to the diffraction pattern To summarize: Real Lattice Decoration of the lattice with motif Real Crystal Purely Geometrical Construction Reciprocal Lattice Decoration of the reciprocal lattice with Intensities Structure factor calculation Reciprocal Crystal Ewald Sphere construction Selection of some spots/intensities from the reciprocal crystal* Diffraction Pattern** In crystals based on a particular lattice the intensities of particular reflections are modified they may even go missing Position of the diffraction spots Intensity of the diffraction spots de s I mi r te ne y b d Lattice Motif Crystal = Lattice + Motif Diffraction Pattern Position of the diffraction spots RECIPROCAL LATTICE Intensity of the diffraction spots MOTIF’ OF INTENSITIES * In fact the Ewald sphere construction selects regions of the reciprocal space (which contains the Bragg diffraction pattern from the crystal(s) and diffuse intensities (between the Bragg peaks). ** The actual diffraction pattern observed in an experiment depends on the ‘detector setup’.

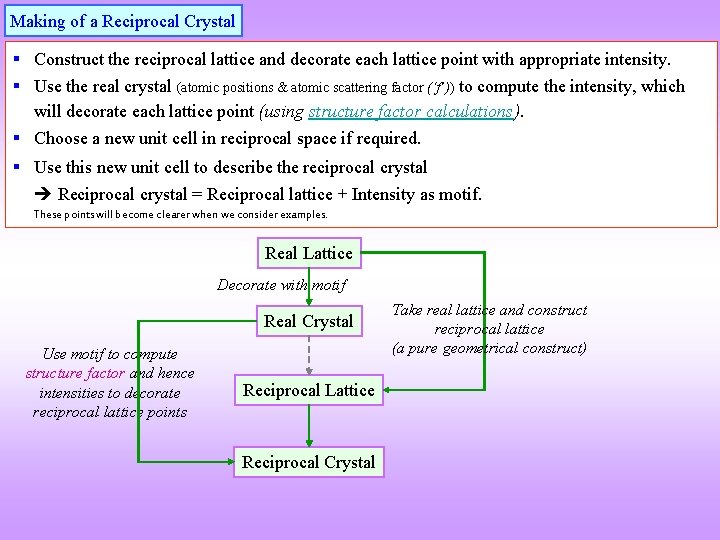
Making of a Reciprocal Crystal § Construct the reciprocal lattice and decorate each lattice point with appropriate intensity. § Use the real crystal (atomic positions & atomic scattering factor (‘f’)) to compute the intensity, which will decorate each lattice point (using structure factor calculations). § Choose a new unit cell in reciprocal space if required. § Use this new unit cell to describe the reciprocal crystal Reciprocal crystal = Reciprocal lattice + Intensity as motif. These points will become clearer when we consider examples. Real Lattice Decorate with motif Real Crystal Use motif to compute structure factor and hence intensities to decorate reciprocal lattice points Reciprocal Lattice Reciprocal Crystal Take real lattice and construct reciprocal lattice (a pure geometrical construct)

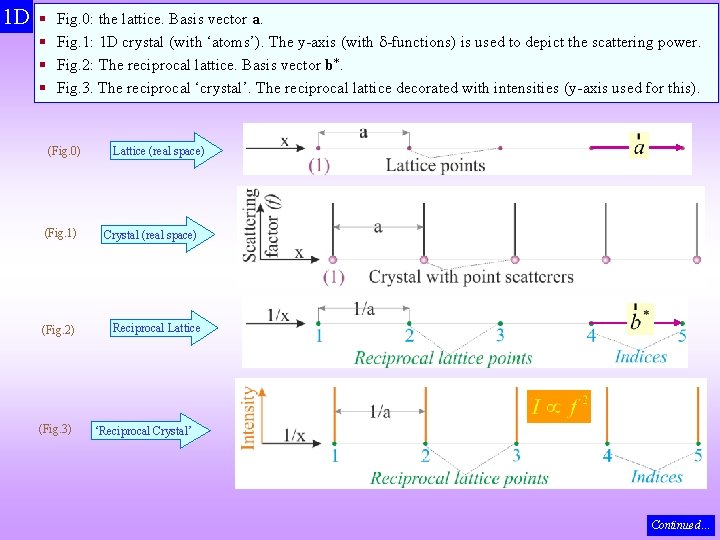
Reciprocal crystal in 1 D (& 2 D) q Let us consider a 1 D lattice with lattice parameter ‘a’ (Fig. 0, next slide). Patch of an infinite lattice shown. The lattice points also correspond to the set of (1) planes. q Let us decorate this lattice with point scatterers (i. e. we do not have to consider the dimension of the scatteres) (Fig. 1). The scattering factor (f) is shown as -functions at each lattice point (y-axis). This is equivalent to the atomic scattering factor for atoms. q The reciprocal lattice can be constructed from the real lattice (Fig. 2). The x-axis has dimensions of [1/distance] and lattice spacing is 1/a. The reciprocal lattice points have been indexed as 1, 2, 3, etc. , which correspond to (1) , (2), (3) ‘planes’ (actually points in 1 D) in the real space lattice. q The reciprocal crystal is constructed from the reciprocal lattice by weighing the same with intensities (i. e. structure factor). This is shown as -functions along the y-axis (Fig. 3). Continued…

1 D § § Fig. 0: the lattice. Basis vector a. Fig. 1: 1 D crystal (with ‘atoms’). The y-axis (with -functions) is used to depict the scattering power. Fig. 2: The reciprocal lattice. Basis vector b*. Fig. 3. The reciprocal ‘crystal’. The reciprocal lattice decorated with intensities (y-axis used for this). (Fig. 0) Lattice (real space) (Fig. 1) Crystal (real space) (Fig. 2) Reciprocal Lattice (Fig. 3) ‘Reciprocal Crystal’ Continued…

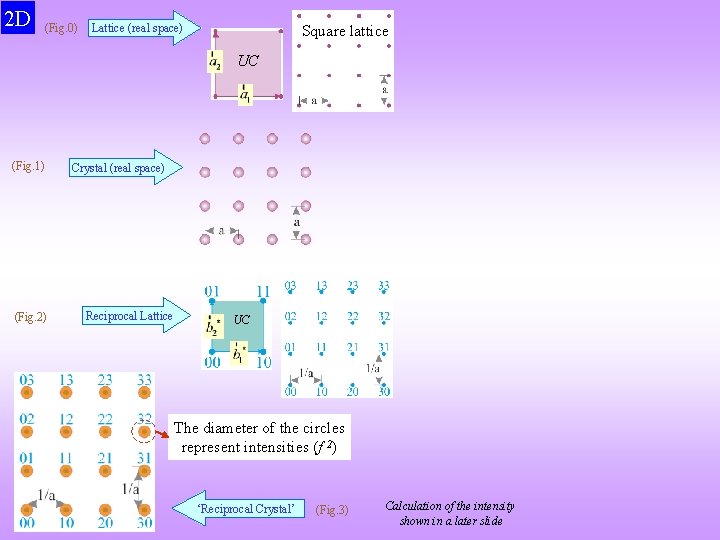
2 D (Fig. 0) Lattice (real space) Square lattice UC (Fig. 1) (Fig. 2) Crystal (real space) Reciprocal Lattice UC The diameter of the circles represent intensities (f 2) ‘Reciprocal Crystal’ (Fig. 3) Calculation of the intensity shown in a later slide

Q&A How to calculate the intensities, which decorate the reciprocal lattice (say in 2 D)? § We have to perform structure factor calculations (click here: Structure Factor Calculations). § For this we use the formula as below. In 3 D In 2 D Meaning of the terms is explained in the slides on Structure Factor Calculations There is only one ‘atom’ (scatterer) at (0, 0) For the square crystal At each reciprocal lattice point resides an intensity f 2

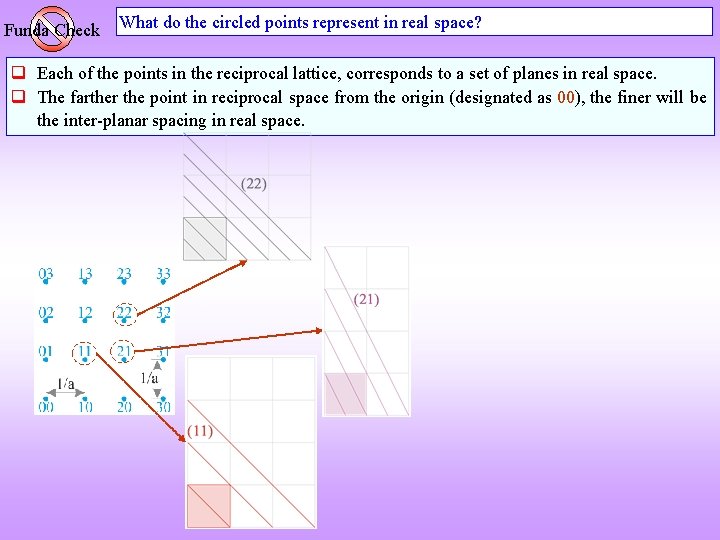
Funda Check What do the circled points represent in real space? q Each of the points in the reciprocal lattice, corresponds to a set of planes in real space. q The farther the point in reciprocal space from the origin (designated as 00), the finer will be the inter-planar spacing in real space.

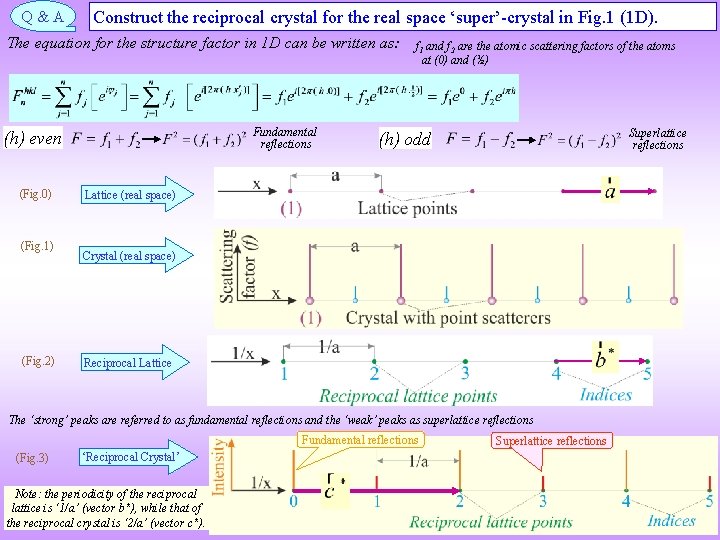
Q&A Construct the reciprocal crystal for the real space ‘super’-crystal in Fig. 1 (1 D). The equation for the structure factor in 1 D can be written as: Fundamental reflections (h) even (Fig. 0) (Fig. 1) (Fig. 2) f 1 and f 2 are the atomic scattering factors of the atoms at (0) and (½) Superlattice reflections (h) odd Lattice (real space) Crystal (real space) Reciprocal Lattice The ‘strong’ peaks are referred to as fundamental reflections and the ‘weak’ peaks as superlattice reflections Fundamental reflections (Fig. 3) ‘Reciprocal Crystal’ Note: the periodicity of the reciprocal lattice is ‘ 1/a’ (vector b*), while that of the reciprocal crystal is ‘ 2/a’ (vector c*). Superlattice reflections

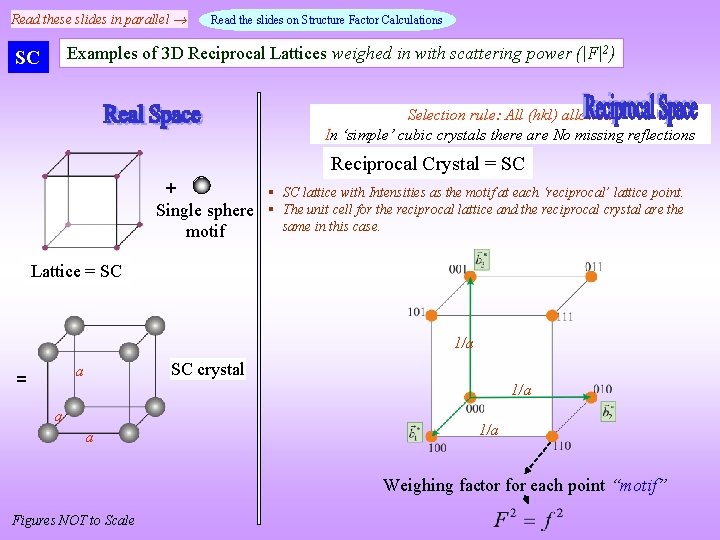
Read these slides in parallel Read the slides on Structure Factor Calculations Examples of 3 D Reciprocal Lattices weighed in with scattering power (|F|2) SC Selection rule: All (hkl) allowed In ‘simple’ cubic crystals there are No missing reflections Reciprocal Crystal = SC + § Single sphere § motif SC lattice with Intensities as the motif at each ‘reciprocal’ lattice point. The unit cell for the reciprocal lattice and the reciprocal crystal are the same in this case. Lattice = SC 1/a SC crystal a = 1/a a a 1/a Weighing factor for each point “motif” Figures NOT to Scale

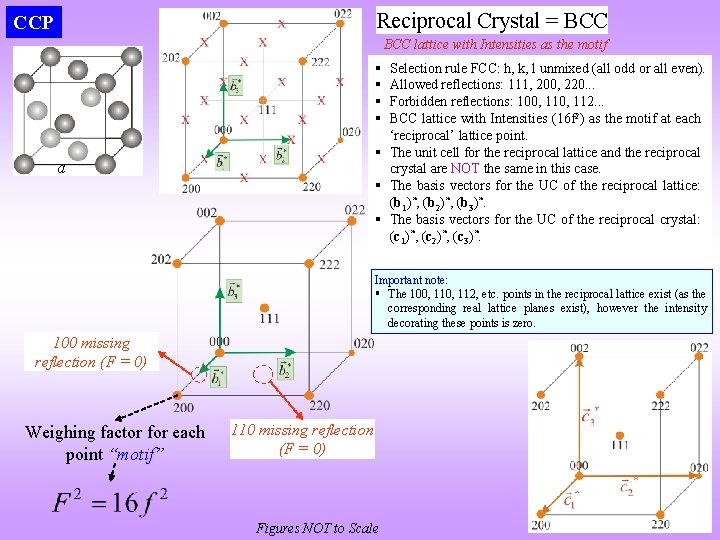
Reciprocal Crystal = BCC CCP BCC lattice with Intensities as the motif § § Selection rule FCC: h, k, l unmixed (all odd or all even). Allowed reflections: 111, 200, 220. . . Forbidden reflections: 100, 112. . . BCC lattice with Intensities (16 f 2) as the motif at each ‘reciprocal’ lattice point. § The unit cell for the reciprocal lattice and the reciprocal crystal are NOT the same in this case. § The basis vectors for the UC of the reciprocal lattice: (b 1)*, (b 2)*, (b 3)*. § The basis vectors for the UC of the reciprocal crystal: (c 1)*, (c 2)*, (c 3)*. a Important note: § The 100, 112, etc. points in the reciprocal lattice exist (as the corresponding real lattice planes exist), however the intensity decorating these points is zero. 100 missing reflection (F = 0) Weighing factor for each point “motif” 110 missing reflection (F = 0) Figures NOT to Scale

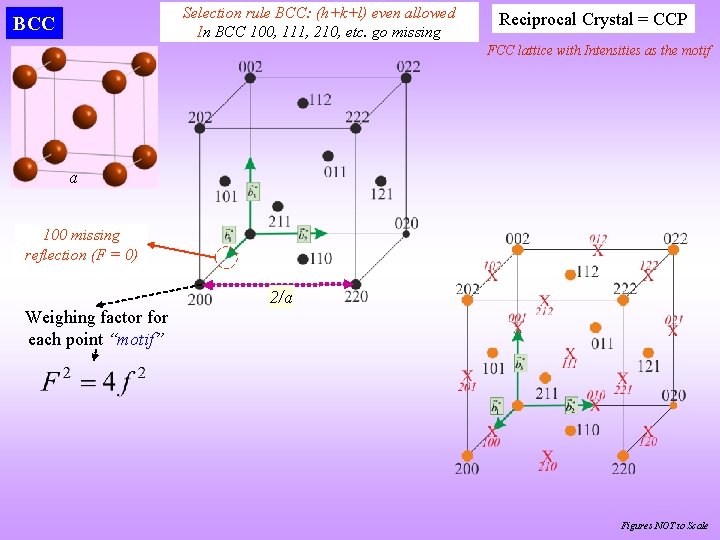
Selection rule BCC: (h+k+l) even allowed In BCC 100, 111, 210, etc. go missing BCC Reciprocal Crystal = CCP FCC lattice with Intensities as the motif a 100 missing reflection (F = 0) 2/a Weighing factor for each point “motif” Figures NOT to Scale

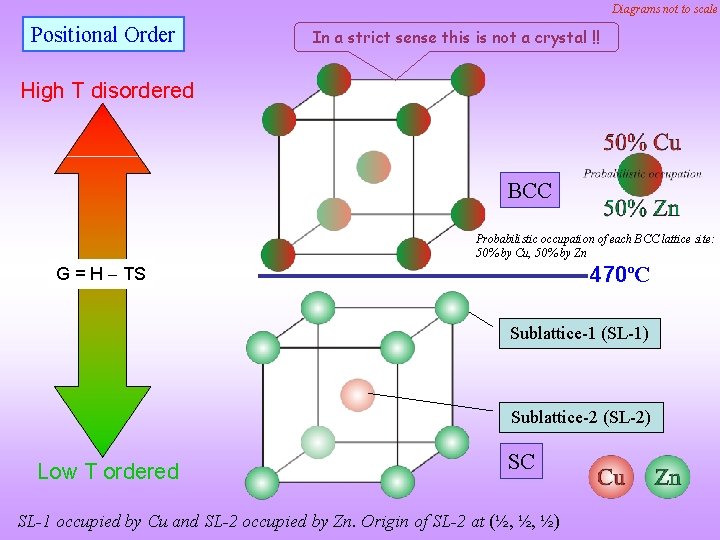
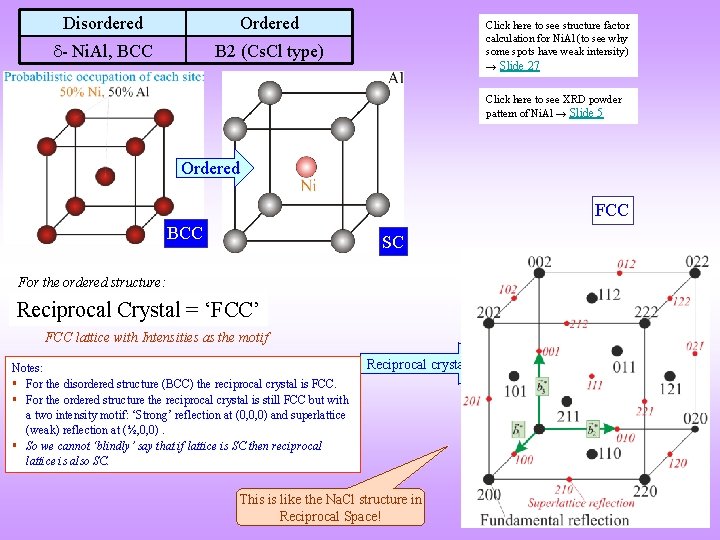
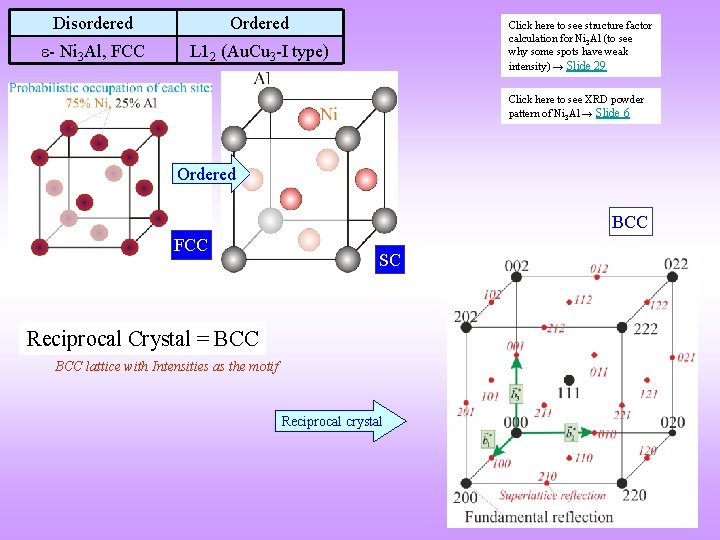
Order-disorder transformation and its effect on diffraction pattern q When a disordered structure becomes an ordered structure (at lower temperature), the symmetry of the structure is lowered and certain superlattice spots appear in the Reciprocal Lattice/crystal (and correspondingly in the appropriate diffraction patterns). Superlattice spots are weaker in intensity than the spots in the disordered structure. q An example of an order-disorder transformation is in the Cu-Zn system: the high temperature structure can be referred to the BCC lattice and the low temperature structure to the SC lattice (as shown next). Another examples are as below. q The phenomenon is associated with diffuse scattering (presence of lower ‘diffuse’ intensity) between the Braggs’ peaks. This is not considered here. Disordered Ordered - Ni. Al, BCC B 2 (Cs. Cl type) - Ni 3 Al, FCC L 12 (Au. Cu 3 -I type) Click here to know more about Superlattices & Sublattices Click here to know more about Ordered Structures

Diagrams not to scale Positional Order In a strict sense this is not a crystal !! High T disordered BCC Probabilistic occupation of each BCC lattice site: 50% by Cu, 50% by Zn 470ºC G = H TS Sublattice-1 (SL-1) Sublattice-2 (SL-2) Low T ordered SC SL-1 occupied by Cu and SL-2 occupied by Zn. Origin of SL-2 at (½, ½, ½)

Disordered Ordered - Ni. Al, BCC B 2 (Cs. Cl type) Click here to see structure factor calculation for Ni. Al (to see why some spots have weak intensity) → Slide 27 Click here to see XRD powder pattern of Ni. Al → Slide 5 Ordered FCC BCC SC For the ordered structure: Reciprocal Crystal = ‘FCC’ FCC lattice with Intensities as the motif Notes: § For the disordered structure (BCC) the reciprocal crystal is FCC. § For the ordered structure the reciprocal crystal is still FCC but with a two intensity motif: ‘Strong’ reflection at (0, 0, 0) and superlattice (weak) reflection at (½, 0, 0). § So we cannot ‘blindly’ say that if lattice is SC then reciprocal lattice is also SC. Reciprocal crystal This is like the Na. Cl structure in Reciprocal Space!

Disordered Ordered - Ni 3 Al, FCC L 12 (Au. Cu 3 -I type) Click here to see structure factor calculation for Ni 3 Al (to see why some spots have weak intensity) → Slide 29 Click here to see XRD powder pattern of Ni 3 Al → Slide 6 Ordered BCC FCC SC Reciprocal Crystal = BCC lattice with Intensities as the motif Reciprocal crystal

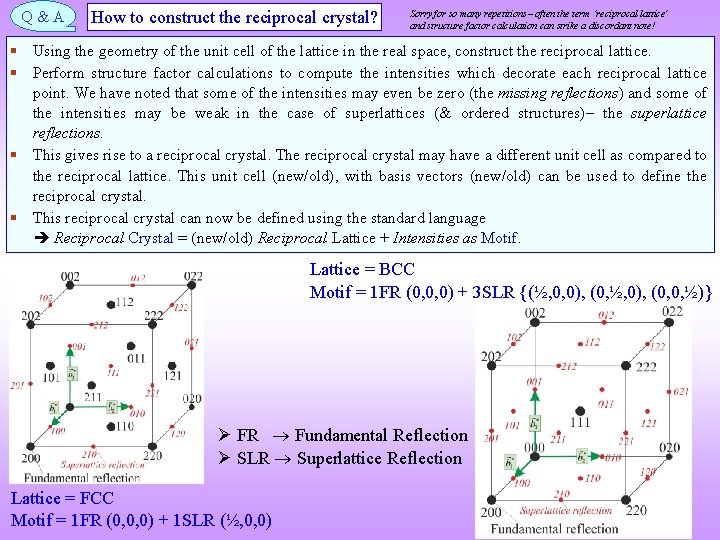
Q&A How to construct the reciprocal crystal? Sorry for so many repetitions often the term ‘reciprocal lattice’ and structure factor calculation can strike a discordant note! § Using the geometry of the unit cell of the lattice in the real space, construct the reciprocal lattice. § Perform structure factor calculations to compute the intensities which decorate each reciprocal lattice point. We have noted that some of the intensities may even be zero (the missing reflections) and some of the intensities may be weak in the case of superlattices (& ordered structures) the superlattice reflections. § This gives rise to a reciprocal crystal. The reciprocal crystal may have a different unit cell as compared to the reciprocal lattice. This unit cell (new/old), with basis vectors (new/old) can be used to define the reciprocal crystal. § This reciprocal crystal can now be defined using the standard language Reciprocal Crystal = (new/old) Reciprocal Lattice + Intensities as Motif. Lattice = BCC Motif = 1 FR (0, 0, 0) + 3 SLR {(½, 0, 0), (0, ½, 0), (0, 0, ½)} FR Fundamental Reflection SLR Superlattice Reflection Lattice = FCC Motif = 1 FR (0, 0, 0) + 1 SLR (½, 0, 0)

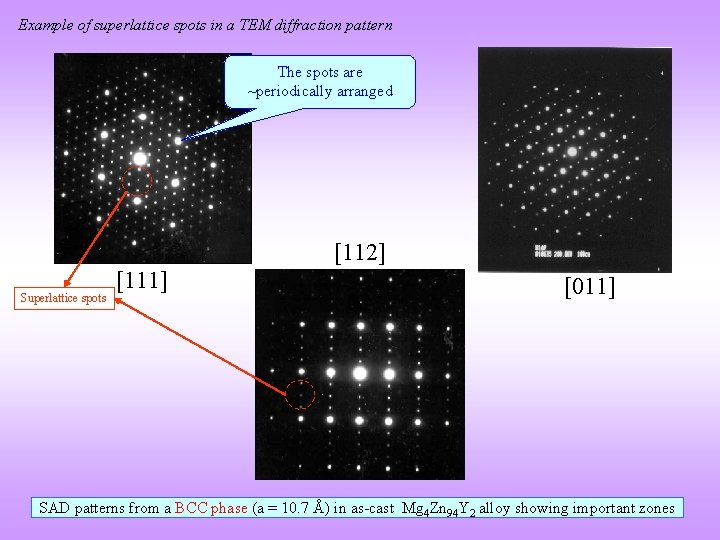
Example of superlattice spots in a TEM diffraction pattern The spots are ~periodically arranged [112] Superlattice spots [111] [011] SAD patterns from a BCC phase (a = 10. 7 Å) in as-cast Mg 4 Zn 94 Y 2 alloy showing important zones

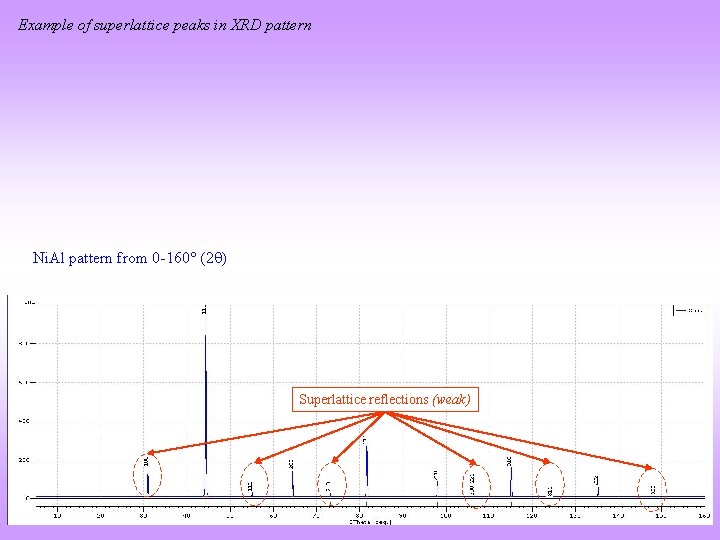
Example of superlattice peaks in XRD pattern Ni. Al pattern from 0 -160 (2 ) Superlattice reflections (weak)

The Ewald Sphere * Paul Peter Ewald (German physicist and crystallographer; 1888 -1985) q The reciprocal crystal is a map of the crystal in reciprocal space → but it does not tell us which spots/reflections would be observed in an actual experiment. q The Ewald sphere construction selects those points/regions of reciprocal space, which can be observed in a diffraction experiment. q The intensities which may be actually observed in a diffraction experiments depends on the ‘detection system’. Circular of a Colloquium held at Max-Planck-Institut für Metallforschung (in honour of Prof. Ewald) 7. Paul-Peter-Ewald-Kolloquium Freitag, 17. Juli 2008 13: 30 Joachim Spatz (Max-Planck-Institut für Metallforschung) Begrüßung 13: 45 Heribert Knorr (Ministerium für Wissenschaft, Forschung und Kunst Baden-Württemberg Begrüßung 14: 00 Stefan Hell (Max-Planck-Institut für Biophysikalische Chemie) Nano-Auflösung mit fokussiertem Licht 14: 30 Antoni Tomsia (Lawrence Berkeley National Laboratory) Using Ice to Mimic Nacre: From Structural Materials to Artificial Bone 15: 00 Pause Kaffee und Getränke 15: 30 Frank Gießelmann(Universität Stuttgart) Von ferroelektrischen Fluiden zu geordneten Dispersionen von Nanoröhren: Aktuelle Themen der Flüssigkristallforschung 16: 00 Verleihung des Günter-Petzow-Preises 2008 16: 15 Udo Welzel (Max-Planck-Institut für Metallforschung) Materialien unter Spannung: Ursachen, Messung und Auswirkungen- Freund Feind ab 17: 00 Sommerfest des Max-Planck-Instituts für Metallforschung organisiert von: Max-Planck-Institut für Metallforschung Institut für Theoretische und Angewandte Physik, Institut für Metallkunde, Institut für Nichtmetallische Anorganische Materialien der Universität Stuttgart Programmt

The Reciprocal Lattice & the Ewald Sphere Readers may refer to Cullity’s book (A 15 -4) for a nice account of the same. § The reciprocal lattice points are the values of momentum transfer for which the Bragg’s equation is satisfied. § For diffraction to occur the scattering vector must be equal to a reciprocal lattice vector. § Geometrically if the origin of reciprocal space is placed at the tip of ki then diffraction will occur only for those reciprocal lattice points that lie on the surface of the Ewald sphere. § Here, for illustration, we consider a 2 D section thought the Ewald Sphere (the ‘Ewald Circle’). Construction of the Ewald sphere is considered next. Bragg’s equation revisited This is Bragg’s equation in reciprocal space Rewrite § Draw a circle with diameter 2/ § Construct a triangle with the diameter as the hypotenuse and 1/dhkl as a side: AOP (any triangle inscribed in a circle with the diameter as the hypotenuse is a right angle triangle: APO = 90 ): § The angle opposite the 1/d side is hkl (from the rewritten Bragg’s equation)

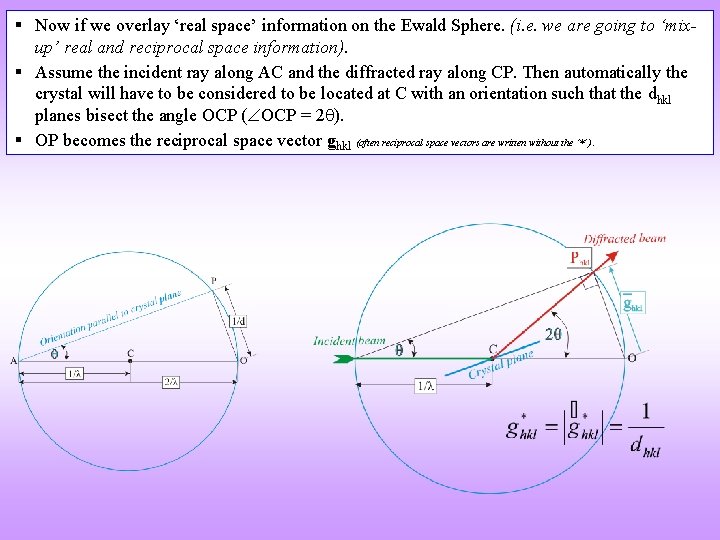
§ Now if we overlay ‘real space’ information on the Ewald Sphere. (i. e. we are going to ‘mixup’ real and reciprocal space information). § Assume the incident ray along AC and the diffracted ray along CP. Then automatically the crystal will have to be considered to be located at C with an orientation such that the dhkl planes bisect the angle OCP ( OCP = 2 ). § OP becomes the reciprocal space vector ghkl (often reciprocal space vectors are written without the ‘*’).

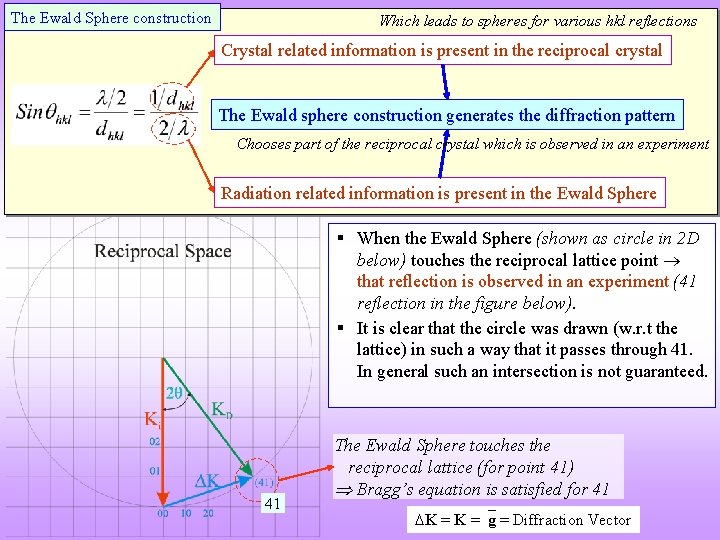
The Ewald Sphere construction Which leads to spheres for various hkl reflections Crystal related information is present in the reciprocal crystal The Ewald sphere construction generates the diffraction pattern Chooses part of the reciprocal crystal which is observed in an experiment Radiation related information is present in the Ewald Sphere § When the Ewald Sphere (shown as circle in 2 D below) touches the reciprocal lattice point that reflection is observed in an experiment (41 reflection in the figure below). § It is clear that the circle was drawn (w. r. t the lattice) in such a way that it passes through 41. In general such an intersection is not guaranteed. 41 The Ewald Sphere touches the reciprocal lattice (for point 41) Bragg’s equation is satisfied for 41 K = g = Diffraction Vector

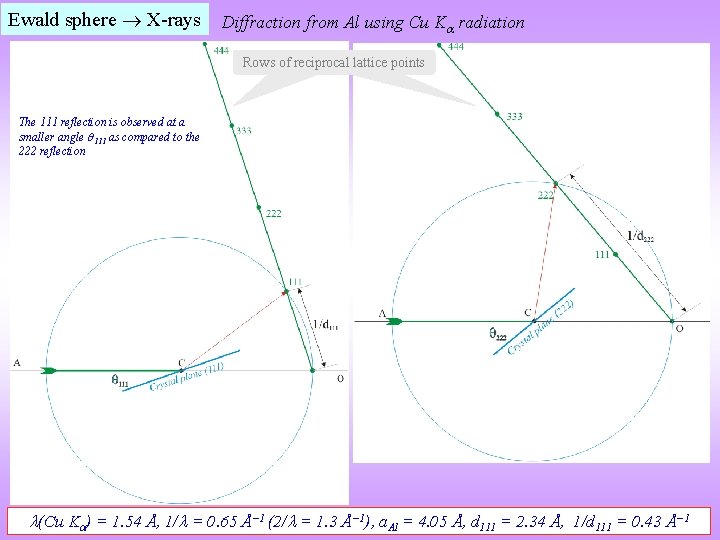
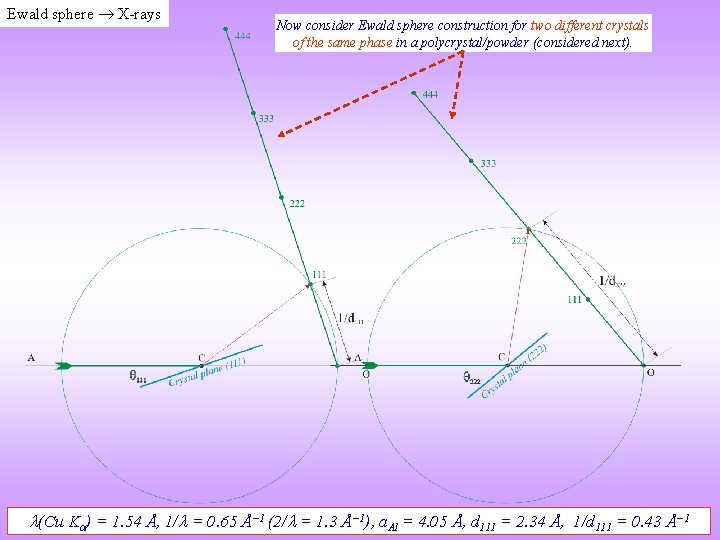
Ewald sphere X-rays Diffraction from Al using Cu K radiation Row of Rows of reciprocal lattice points The 111 reflection is observed at a smaller angle 111 as compared to the 222 reflection (Cu K ) = 1. 54 Å, 1/ = 0. 65 Å− 1 (2/ = 1. 3 Å− 1), a. Al = 4. 05 Å, d 111 = 2. 34 Å, 1/d 111 = 0. 43 Å− 1

Ewald sphere X-rays Now consider Ewald sphere construction for two different crystals of the same phase in a polycrystal/powder (considered next). (Cu K ) = 1. 54 Å, 1/ = 0. 65 Å− 1 (2/ = 1. 3 Å− 1), a. Al = 4. 05 Å, d 111 = 2. 34 Å, 1/d 111 = 0. 43 Å− 1

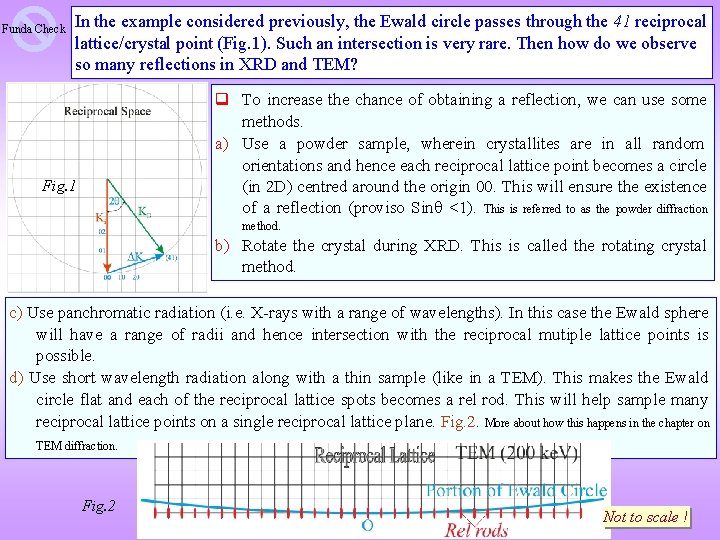
Funda Check In the example considered previously, the Ewald circle passes through the 41 reciprocal lattice/crystal point (Fig. 1). Such an intersection is very rare. Then how do we observe so many reflections in XRD and TEM? q To increase the chance of obtaining a reflection, we can use some methods. a) Use a powder sample, wherein crystallites are in all random orientations and hence each reciprocal lattice point becomes a circle (in 2 D) centred around the origin 00. This will ensure the existence of a reflection (proviso Sin <1). This is referred to as the powder diffraction Fig. 1 method. b) Rotate the crystal during XRD. This is called the rotating crystal method. c) Use panchromatic radiation (i. e. X-rays with a range of wavelengths). In this case the Ewald sphere will have a range of radii and hence intersection with the reciprocal mutiple lattice points is possible. d) Use short wavelength radiation along with a thin sample (like in a TEM). This makes the Ewald circle flat and each of the reciprocal lattice spots becomes a rel rod. This will help sample many reciprocal lattice points on a single reciprocal lattice plane. Fig. 2. More about how this happens in the chapter on TEM diffraction. Fig. 2 Not to scale !

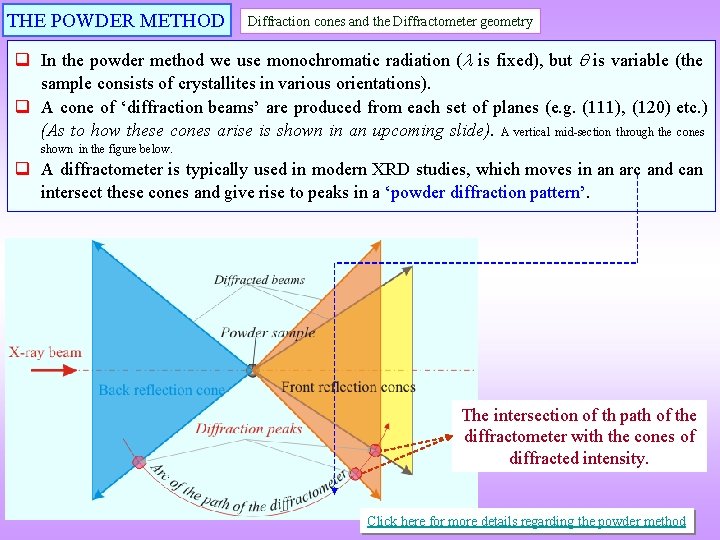
THE POWDER METHOD Diffraction cones and the Diffractometer geometry q In the powder method we use monochromatic radiation ( is fixed), but is variable (the sample consists of crystallites in various orientations). q A cone of ‘diffraction beams’ are produced from each set of planes (e. g. (111), (120) etc. ) (As to how these cones arise is shown in an upcoming slide). A vertical mid-section through the cones shown in the figure below. q A diffractometer is typically used in modern XRD studies, which moves in an arc and can intersect these cones and give rise to peaks in a ‘powder diffraction pattern’. The intersection of th path of the diffractometer with the cones of diffracted intensity. Click here for more details regarding the powder method

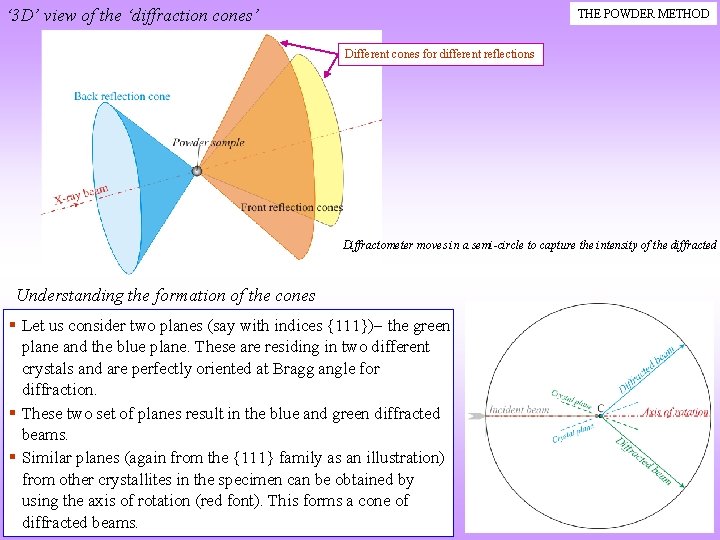
‘ 3 D’ view of the ‘diffraction cones’ THE POWDER METHOD Different cones for different reflections Diffractometer moves in a semi-circle to capture the intensity of the diffracted Understanding the formation of the cones § Let us consider two planes (say with indices {111}) the green plane and the blue plane. These are residing in two different crystals and are perfectly oriented at Bragg angle for diffraction. § These two set of planes result in the blue and green diffracted beams. § Similar planes (again from the {111} family as an illustration) from other crystallites in the specimen can be obtained by using the axis of rotation (red font). This forms a cone of diffracted beams.

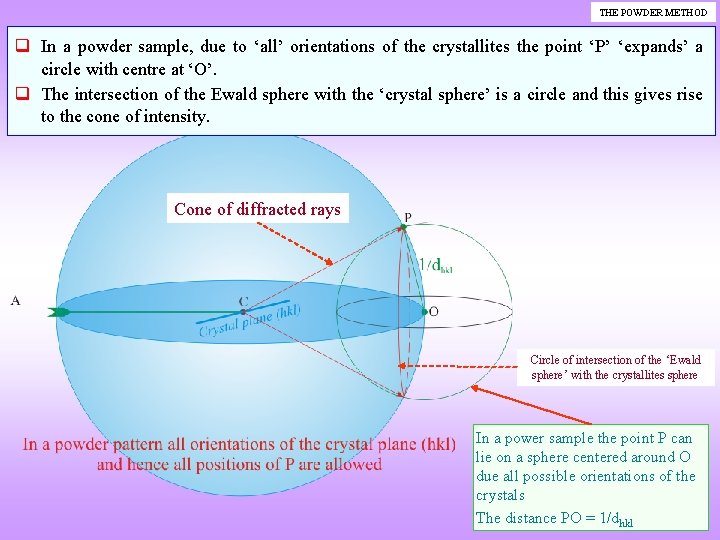
THE POWDER METHOD q In a powder sample, due to ‘all’ orientations of the crystallites the point ‘P’ ‘expands’ a circle with centre at ‘O’. q The intersection of the Ewald sphere with the ‘crystal sphere’ is a circle and this gives rise to the cone of intensity. Cone of diffracted rays Circle of intersection of the ‘Ewald sphere’ with the crystallites sphere In a power sample the point P can lie on a sphere centered around O due all possible orientations of the crystals The distance PO = 1/dhkl

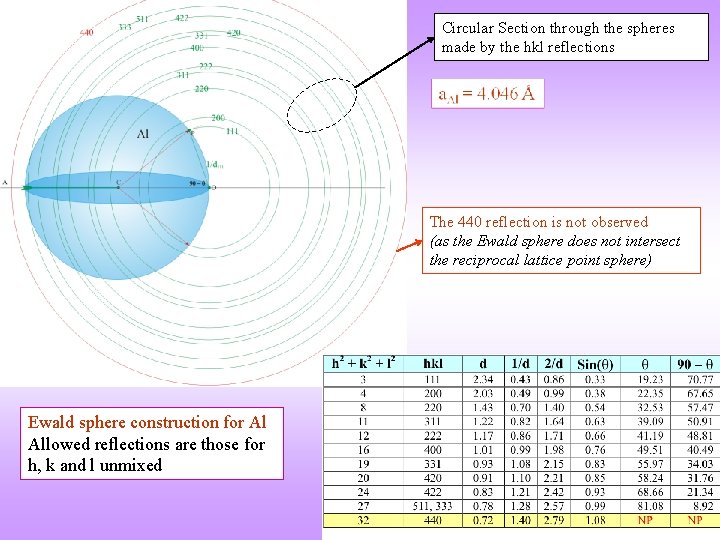
Circular Section through the spheres made by the hkl reflections The 440 reflection is not observed (as the Ewald sphere does not intersect the reciprocal lattice point sphere) Ewald sphere construction for Al Allowed reflections are those for h, k and l unmixed

The 331 reflection is not observed Ewald sphere construction for Cu Allowed reflections are those for h, k and l unmixed

End

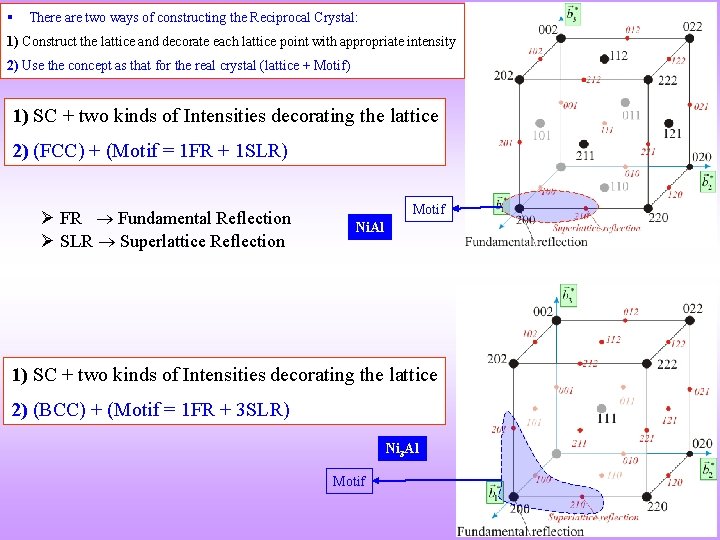
§ There are two ways of constructing the Reciprocal Crystal: 1) Construct the lattice and decorate each lattice point with appropriate intensity 2) Use the concept as that for the real crystal (lattice + Motif) 1) SC + two kinds of Intensities decorating the lattice 2) (FCC) + (Motif = 1 FR + 1 SLR) FR Fundamental Reflection SLR Superlattice Reflection Motif Ni. Al 1) SC + two kinds of Intensities decorating the lattice 2) (BCC) + (Motif = 1 FR + 3 SLR) Ni 3 Al Motif

q The above two approaches are equivalent for simple crystals (SC, BCC, FCC lattices decorated with monoatomic motifs), but for ordered crystals the two approaches are different (E. g. ordered Cu. Zn, Ordered Ni 3 Al etc. ) (as shown soon). * Point #1 has been considered to be consistent with literature– though this might be inappropriate. ** Point #2 makes reciprocal crystals equivalent in definition to real crystals
 Ewald construction in reciprocal lattice
Ewald construction in reciprocal lattice Poset matematika diskrit
Poset matematika diskrit Sphere of control
Sphere of control Reciprocal lattice vector
Reciprocal lattice vector Reciprocal lattice
Reciprocal lattice Reciprocal lattice concept in x ray diffraction
Reciprocal lattice concept in x ray diffraction Reciprocal metric tensor
Reciprocal metric tensor Laue equation
Laue equation Reciprocal lattice
Reciprocal lattice Reciprocal lattice
Reciprocal lattice Ewald tube
Ewald tube Ewald korevaar
Ewald korevaar Andrew ewald st louis park
Andrew ewald st louis park Rsce21
Rsce21 Sonda ewald
Sonda ewald Levacuator tube
Levacuator tube Ewald's first law
Ewald's first law Ewald-oseen extinction theorem
Ewald-oseen extinction theorem Tipologi kepribadian
Tipologi kepribadian Ewald tube
Ewald tube Uwe ewald
Uwe ewald Jessica ewald
Jessica ewald Ewald hettema
Ewald hettema Ewald summation
Ewald summation Gawlik śląski malarz
Gawlik śląski malarz There's a place where mercy reigns
There's a place where mercy reigns Lattice method multiplication calculator
Lattice method multiplication calculator Lattice structure of sodium chloride
Lattice structure of sodium chloride Lattice vibrations
Lattice vibrations Permutohedral lattice
Permutohedral lattice Mark kasevich
Mark kasevich Types of crystal imperfections
Types of crystal imperfections What is hydration enthalpy
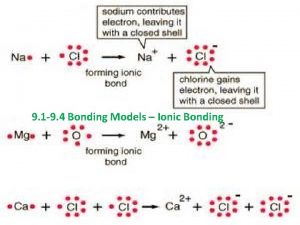
What is hydration enthalpy Giant ionic bonding
Giant ionic bonding Lattice beam design
Lattice beam design Dhsub
Dhsub Blp lattice
Blp lattice Lattice plan
Lattice plan Lattices and boolean algebra
Lattices and boolean algebra Lingual apron rpd
Lingual apron rpd Lattice vibrations
Lattice vibrations Partial products multiplication
Partial products multiplication Lattice multiplication
Lattice multiplication Magnitude of lattice energy
Magnitude of lattice energy Taylor lattice
Taylor lattice Lattice degeneration
Lattice degeneration