Helius composite 2017 Helius composite 2017 Beam subjected

Helius composite 2017
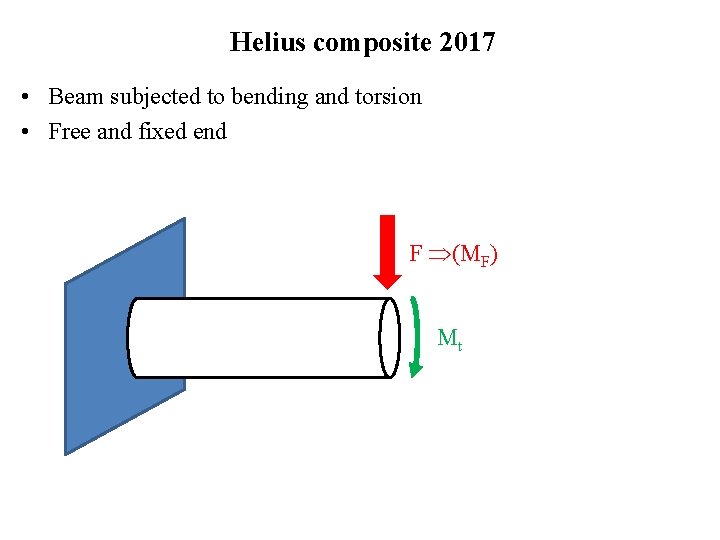
Helius composite 2017 • Beam subjected to bending and torsion • Free and fixed end F (MF) Mt
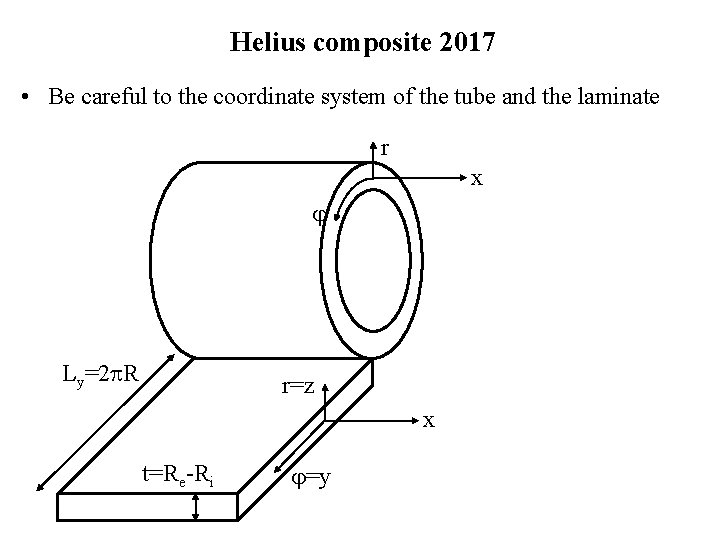
Helius composite 2017 • Be careful to the coordinate system of the tube and the laminate r x Ly=2 R r=z x t=Re-Ri =y

Choice of the orientation angle •

Choice of the thickness • dn x x Neutral axis - x
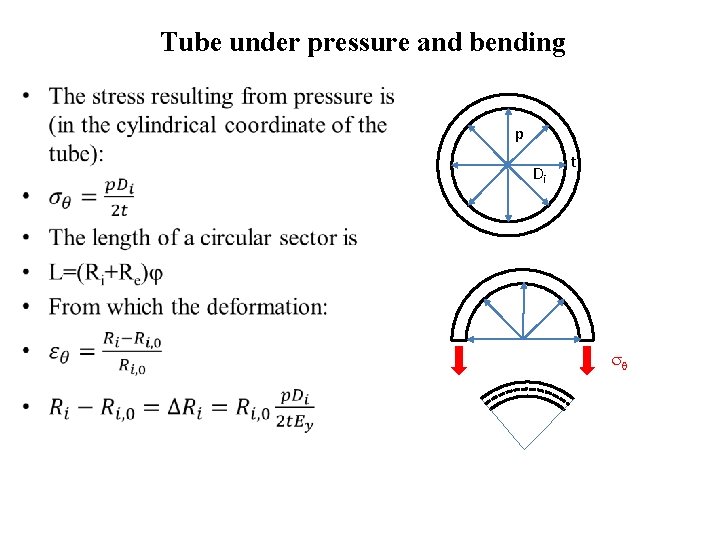
Tube under pressure and bending • p Di t

Tube under pressure and bending •

Tube under pressure and bending •
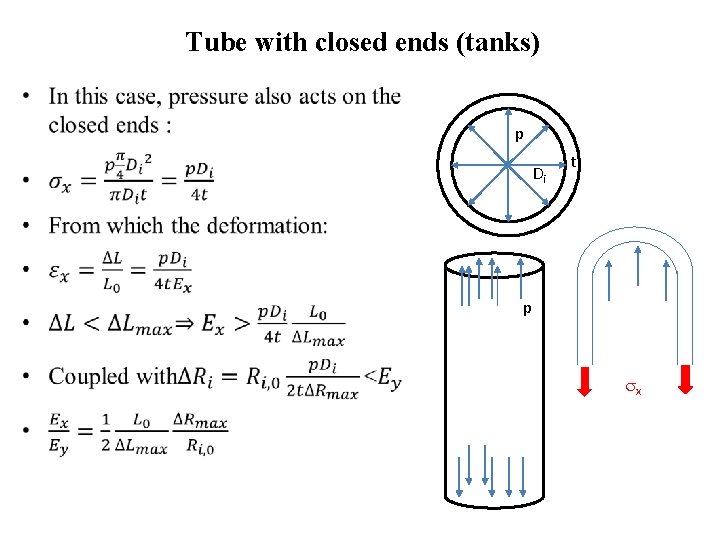
Tube with closed ends (tanks) • p Di t p x

Plate analysis •

Plate analysis •

Plate analysis •

Plate analysis •
Helius composite
Laminate building
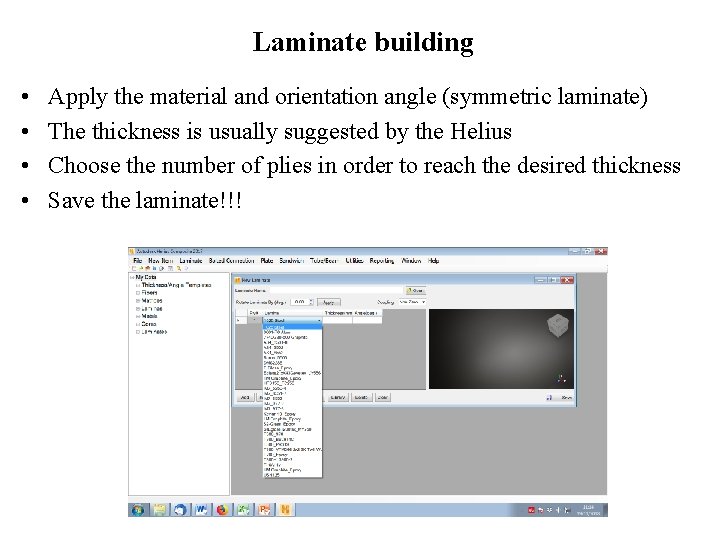
Laminate building • • Apply the material and orientation angle (symmetric laminate) The thickness is usually suggested by the Helius Choose the number of plies in order to reach the desired thickness Save the laminate!!!
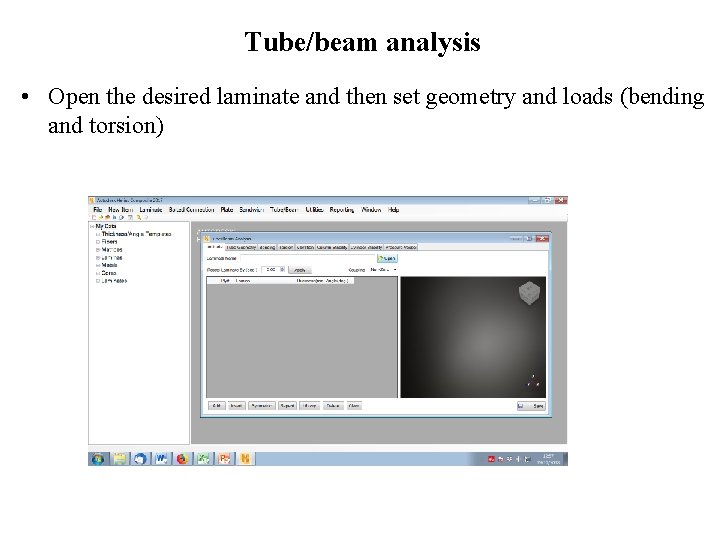
Tube/beam analysis • Open the desired laminate and then set geometry and loads (bending and torsion)
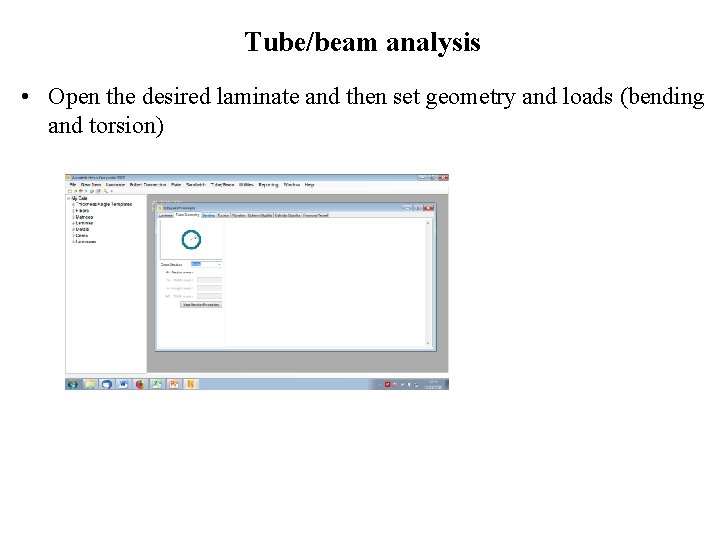
Tube/beam analysis • Open the desired laminate and then set geometry and loads (bending and torsion)
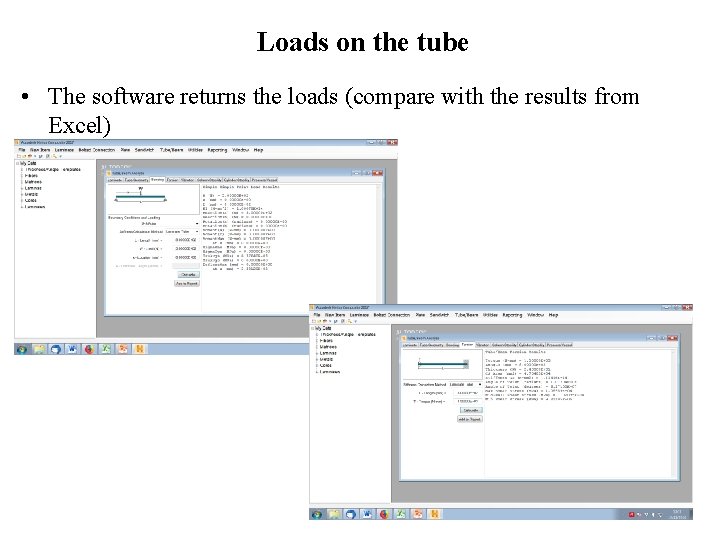
Loads on the tube • The software returns the loads (compare with the results from Excel)
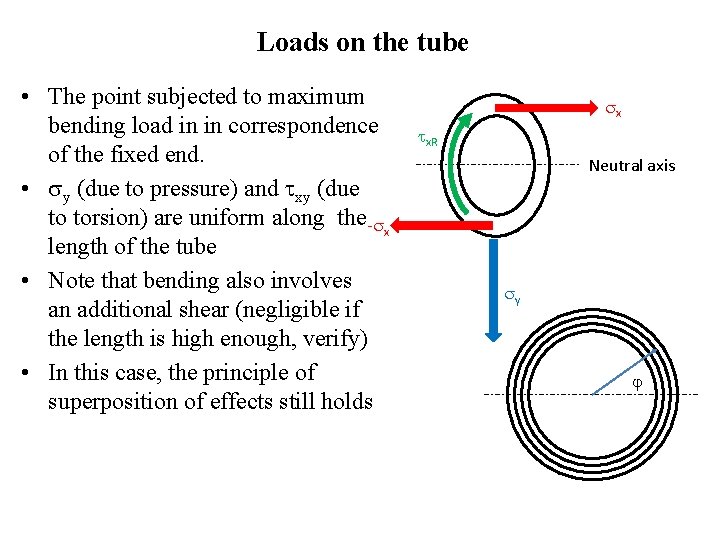
Loads on the tube • The point subjected to maximum bending load in in correspondence of the fixed end. • y (due to pressure) and xy (due to torsion) are uniform along the - x length of the tube • Note that bending also involves an additional shear (negligible if the length is high enough, verify) • In this case, the principle of superposition of effects still holds x x. R Neutral axis y
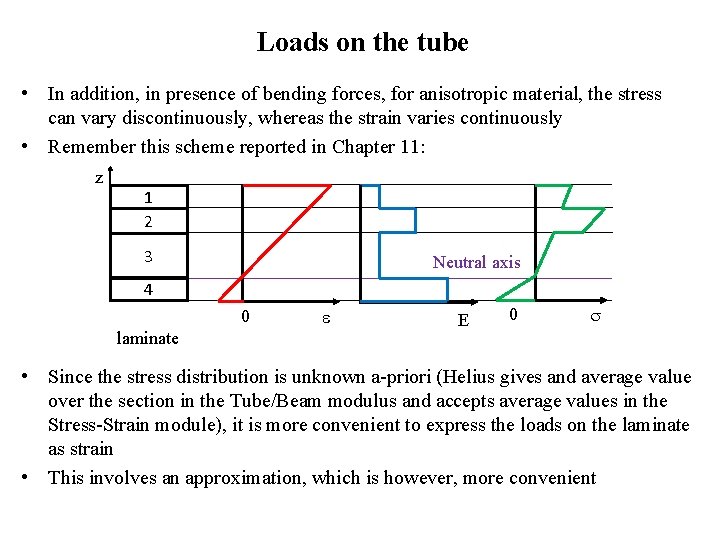
Loads on the tube • In addition, in presence of bending forces, for anisotropic material, the stress can vary discontinuously, whereas the strain varies continuously • Remember this scheme reported in Chapter 11: z 1 2 3 Neutral axis 4 0 laminate E 0 • Since the stress distribution is unknown a-priori (Helius gives and average value over the section in the Tube/Beam modulus and accepts average values in the Stress-Strain module), it is more convenient to express the loads on the laminate as strain • This involves an approximation, which is however, more convenient

Loads on the tube • Now remember that, according to the definitions, x varies along r and , whereas x. R varies along r • If the tube is thin, the variation along r is negligible

Loads on the tube • However, the Helius only allows to consider the middle plane strains:
Loads on the tube • Therefore, the best option is to consider the maximum strains, as they were acting on the whole laminate area • Verify in tension and compression!

Loads on plate • Middle plane
- Slides: 25