Hedonic Prices Allen C Goodman 2000 Hedonic Price

Hedonic Prices © Allen C. Goodman, 2000

Hedonic Price Analysis It became clear in the 1960 s that for many types of analyses one wanted to look at the fact that housing was a multidimensional good. That means that you need to talk about more than simple dollars worth of housing. A list that I have found useful is: – – structure (including lot) neighborhood public services location relative to desirable places. All of these may have numerous dimensions. The key question is whether these are perfect, or even good substitutes, for each other. The answer, it would seem to be is NO.

Born in Detroit The answer, believe it or not, was born in Detroit, in 1938. Andrew Court, an economist for General Motors, was looking for a type of analysis that would compare the prices of cars produced at different times. He argued that size, power, weight, etc. may vary from year to year, so what you wanted to do was to control for these changes in order to get a measure of the valuation of each component, and hence the price change, holding them constant. In the simplest form, you had: P = 0 + 1 Z 1 + 2 Z 2 +. . . + t + , where your Zi are component parts, and t is your time trend.

Uses When large databases became available, it became useful to consider the same type of analysis for several reasons: Real estate assessment - it could be done quickly. Measurement of individual contributions - structure might be easy to measure based on costs, but what about neighborhood? Externalities - If air pollution is important, for example, shouldn't we be able to measure its impact on property values?

P = 0 + 1 Z 1 + 2 Z 2 +. . . + t + , • Should equation be linear? Does the 10 th room impart as much value as the 3 rd room, or the 7 th? • What is the hedonic price of an attribute? A> P/ Zi hedonic price. • What is the meaning of a hedonic price? Is it supply, or demand, or what? • Are the coefficients stable over time? • Should the buyer's or seller's characteristics go into the equation?

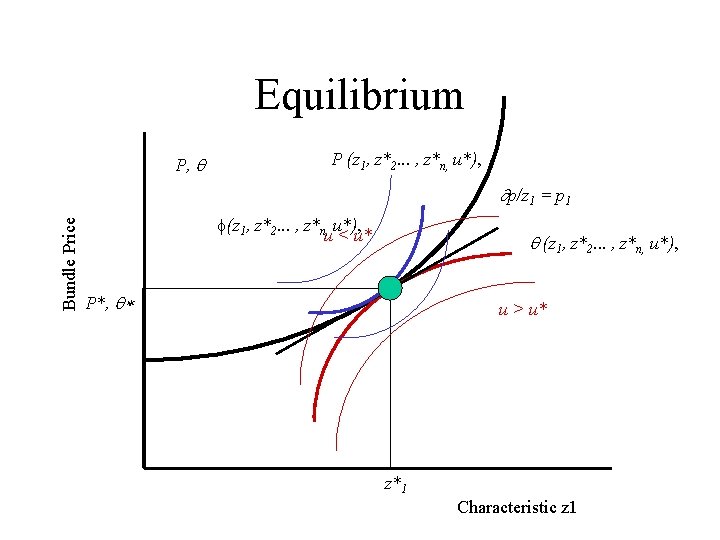
Rosen’s Work • It was in this framework that Rosen's model became most influential. • He mapped out the way that hedonic prices represented the joint envelope of bids (from demand) and offers (from supply). • We're going to show these are derived, and how they change. • Also, it suggests the type of additional information that is necessary to interpret them as pure demand and/or supply parameters.

Analytics Define: p = p (z 1, . . . , zn). Hedonic price is p/zi = pi. Consider consumer's optimization: L = U (x, z 1, . . . , zn) + [y - x - p (z 1, . . . , zn)]. In eq'm: p/ zi = pi = Uzi /Ux.

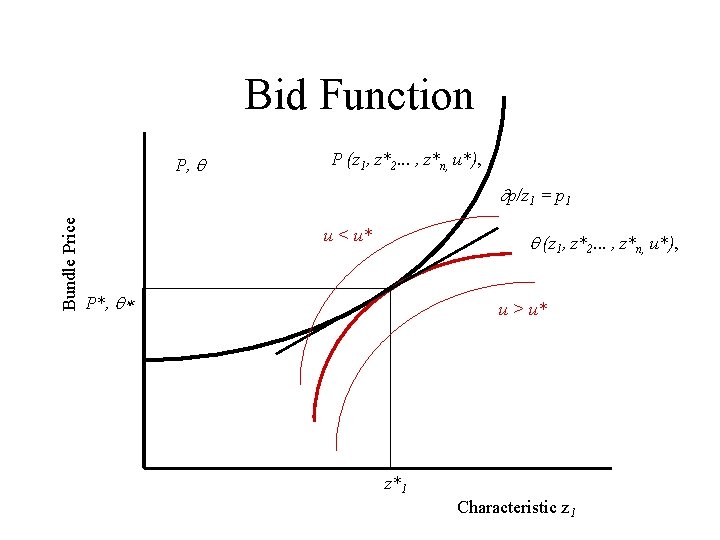
Bid Functions Define “BID” function = (z 1, . . . , zn), such that: U (x, z) = U (y - , z) = u*. (1) Ux (dy - d ) + Uz dz = du* Ux ( y/ zi - / zi) + Uzi = u*/ zi Holding y constant: - Ux / zi + Uzi = 0. / zi = Uzi /Ux. (2) Ux (1 - / y) + Uz z/ y = u* / y Ux (1 - / y) + 0 = 0. / y = 1. (3) Ux ( y/ u* - / u*) + Uz z/ u* = 1. - Ux / u* = 1 / u* = -1/Ux.

Bid Function P, P (z 1, z*2. . . , z*n, u*), Bundle Price p/z 1 = p 1 u < u* (z 1, z*2. . . , z*n, u*), P*, * u > u* z*1 Characteristic z 1

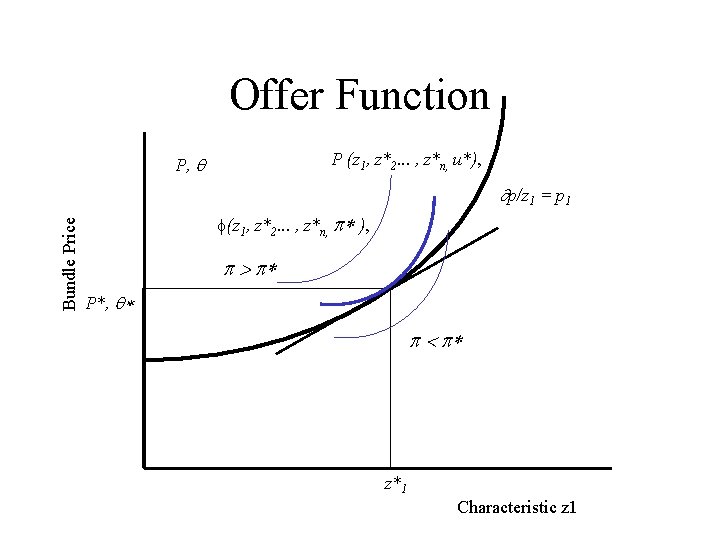
Offer Functions Total costs = C(M, z) M = Number of units (cars, houses) z = composition of units. First: p = M p(z) - C(M, z) First order conditions for profit maximization: (1) p(z) = CM (2) Mpzi = Czi. Leads to: p = M f(z) - C (M, z) d p = M d f+ fd. M - d. C = 0.

Offer (2) (1) p / zi = M f / zi - C/ Zi = 0. f/ zi = ( C/ zi)/M. (2) p / p = 1 = M f / p = 1/M.

Offer Function P (z 1, z*2. . . , z*n, u*), P, Bundle Price p/z 1 = p 1 f(z 1, z*2. . . , z*n, p* ), p > p* P*, * p < p* z*1 Characteristic z 1

Equilibrium P, P (z 1, z*2. . . , z*n, u*), Bundle Price p/z 1 = p 1 f(z 1, z*2. . . , z*n, u*), u < u* (z 1, z*2. . . , z*n, u*), P*, * u > u* z*1 Characteristic z 1

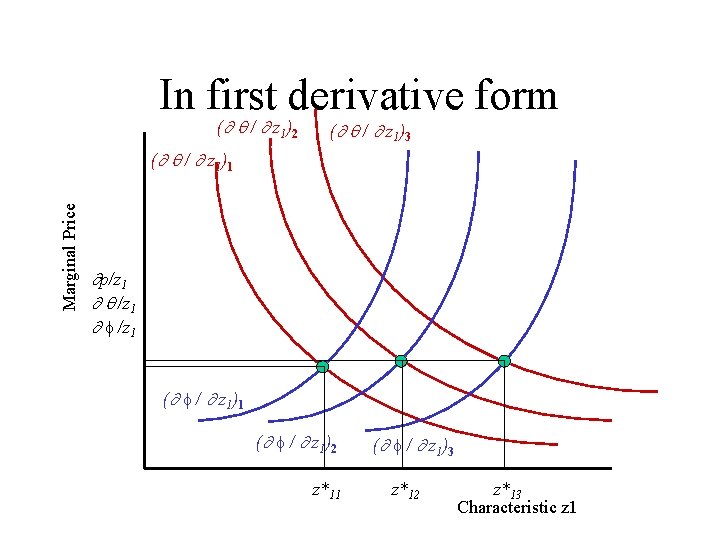
In first derivative form ( / z 1)2 ( / z 1)3 Marginal Price ( / z 1)1 p/z 1 f /z 1 ( f / z 1)2 z*11 ( f / z 1)3 z*12 z*13 Characteristic z 1

Estimation Want to estimate equations to allow enough flexibility for hedonic price functions. One form that has become popular is the Box-Cox estimator. Most generally, you have: (P -1) / = 0 + i (zi i - 1)/ i + . If = 1, and i = 1, we have linear If = 1, and i = 0, we have semilog If = 0, and i = 0, we have log-log. First derivative is the hedonic price: P/ zi = i P 1 - zi i - 1. Second derivative gives envelope of hedonic prices. 2 P/ zi 2 = i (1 - ) P - zi i (1 - i)