HECRAS Basic HECRAS Principles Steady 1 D Flow

HEC-RAS Basic HECRAS Principles ~ Steady 1 D Flow Jon Fripp NDCSMC 2016

Module 2: HEC-RAS – Basic Principles • Hydraulic Analysis Components • What the program does when it runs steady, 1 D simulations We want to be sure everyone is on the same page before we jump into HECRAS applications

A necessary discussion of theory necessitates some coffee

What about water. . . • Incompressible fluid - must increase or decrease its velocity and depth to adjust to the channel shape • High tensile strength - allows it to be drawn smoothly along while accelerating • No shear strength - does not decelerate smoothly, results in standing waves, good canoeing, air entrainment, etc Water is treated as an ideal fluid that behaves according to mathematical/physical principles

What about open channel flow. . . • A free surface • Liquid surface is open to the atmosphere • Boundary is not fixed by the physical boundaries of a closed conduit Being open channel does not make it simpler!

Since the flow is incompressible, the product of the velocity and cross sectional area is a constant. Continuity Equation (conservation of mass) VA = constant Discharge is expressed as Q = VA 5’ Q is flow V is velocity A is cross section area 10’ Velocity = 1 fps Q=VA=1 fps x 5’x 10’= 50 cfs 1’ Velocity = 5 fps Q=VA=5 fps x 1’x 10’= 50 cfs

Open Channel Flow - Controls Definition: A control is any feature of a channel for which a unique depth - discharge relationship occurs. • Weirs/Spillways • Structures • Abrupt changes in slope or width • Friction - over a distance

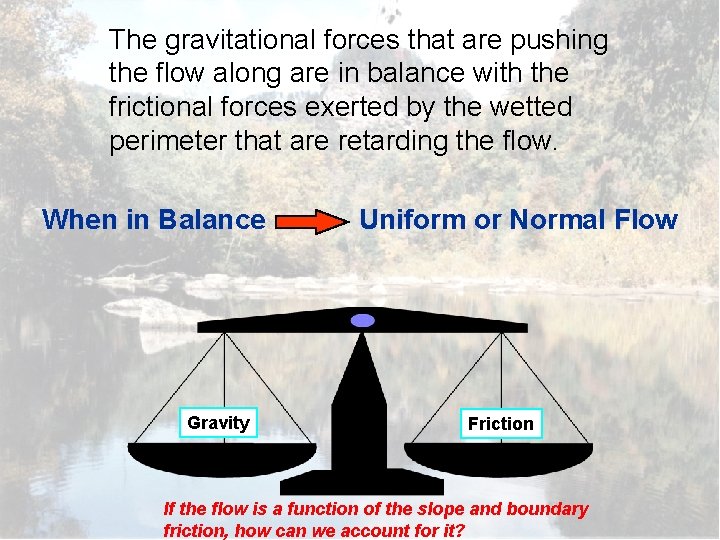
The gravitational forces that are pushing the flow along are in balance with the frictional forces exerted by the wetted perimeter that are retarding the flow. When in Balance Gravity Uniform or Normal Flow Friction If the flow is a function of the slope and boundary friction, how can we account for it?

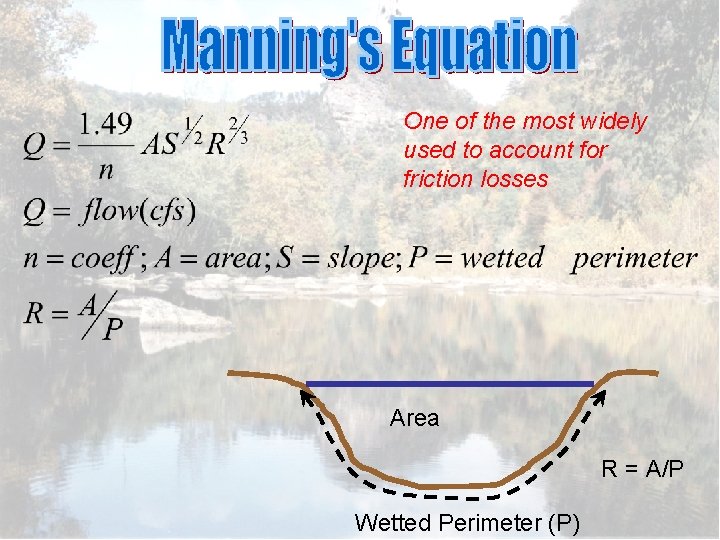
One of the most widely used to account for friction losses Area R = A/P Wetted Perimeter (P)

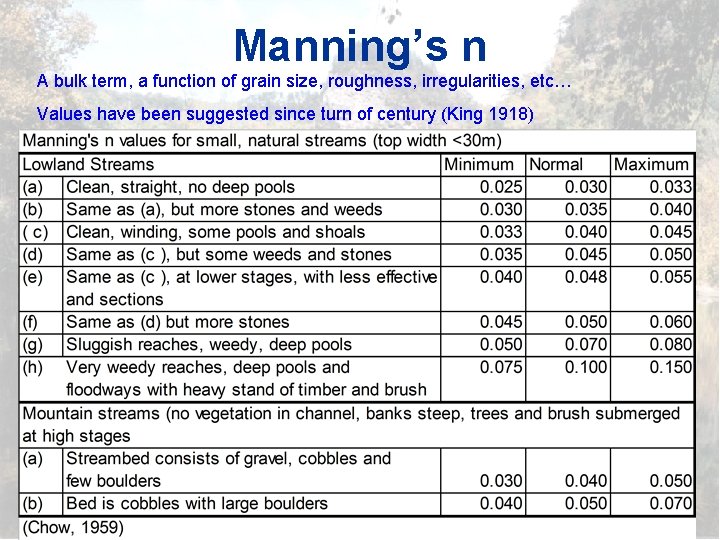
Manning’s n A bulk term, a function of grain size, roughness, irregularities, etc… Values have been suggested since turn of century (King 1918)

Guidance Available (calibrated photographs) n=0. 018 USGS -Water Supply Paper 1849 SCS - Fasken, 1963 n=0. 110 n=0. 050 n=0. 018 n=0. 014 n=0. 060 n=0. 125 n=0. 016 n=0. 080 n=0. 020 n=0. 150

What can we do with Manning’s Equation? Can compute many of the parameters that we are interested in: • Velocity • Trial and error for depth, width, area, etc

So…why make things any more complicated?

How sensitive is the equation? W=100’ d=5’ S=0. 004 n=0. 035 Q=3700 cfs n=0. 03 to 0. 04 13% to 17% d=4. 5 to 5. 5 ft 16% to 17% w =90 to 110 ft 11% S=0. 003 to 0. 005 12% to 13% All 40% to 70% It gets worse!

Limitations of a Normal Depth Computation: • • Constant Section - natural channel? Constant Roughness - overbank flow? Constant Slope No Obstructions - bridges, weirs, etc

Open Channel Flow is typically e varied d a m an ral m u h at t Bo d n nels an an ch Subcritical Critical Supercritical Hydraulic Jump Subcritical Tim Mc. Cabe, IA NRCS Subcritical Critical Supercritical Subcritical Hydraulic Jump F 16 Lynn Betts , IA NRCS

So…. in natural gradually varied flow channels…. Velocity and depth change from section to section. However, the energy and mass are conserved. Simply put – sections and slopes are not constant in natural channels, the flows are not uniform….

HEC-RAS uses the one dimensional energy equation with energy losses due to friction evaluated with Manning’s equation to compute water surface profiles. This is accomplished with an iterative computational procedure called the Standard Step Method

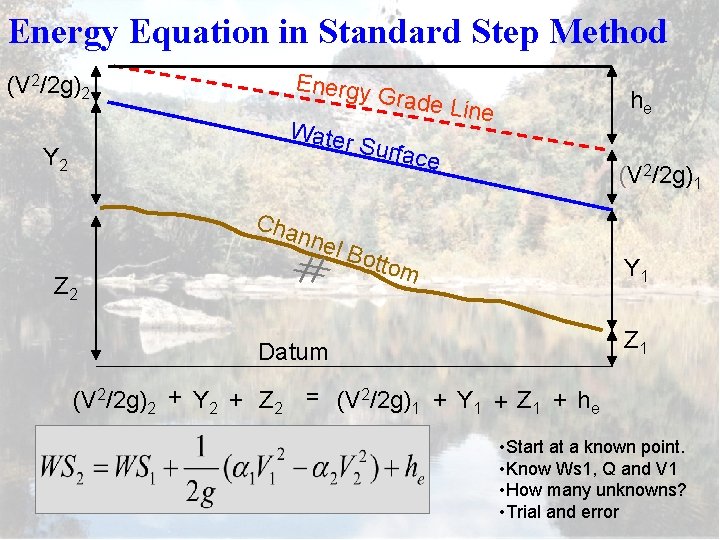
Energy Equation in Standard Step Method (V 2/2 g)2 Energy Water Y 2 Cha nne Z 2 Grade L he ine Surfa ce (V 2/2 g)1 l Bo ttom Y 1 Z 1 Datum (V 2/2 g)2 + Y 2 + Z 2 = (V 2/2 g)1 + Y 1 + Z 1 + he • Start at a known point. • Know Ws 1, Q and V 1 • How many unknowns? • Trial and error

HEC-RAS - Computation Procedure u Assume water surface elevation at upstream/ downstream cross-section. v Based on the assumed water surface elevation, determine the corresponding total conveyance and velocity head w With values from step 2, compute equation for he. and solve x With values from steps 2 and 3, solve energy equation for WS 2. y Compare the computed value of WS 2 with value assumed in step 1; repeat steps 1 through 5 until the values agree to within 0. 01 feet, or the user-defined Simply put – a trial and error approach tolerance.

Energy Loss - important stuff • Loss coefficients Used: – Manning’s n values for friction loss • very significant to accuracy of computed profile • calibrate whenever data is available – Contraction and expansion coefficients for XSections • due to losses associated with changes in X-Section areas and velocities • contraction when velocity increases downstream • expansion when velocity decreases downstream – Bridge and culvert contraction & expansion loss coefficients • same as for X-Sections but usually larger values

Friction loss is evaluated as the product of the friction slope and the discharge weighted reach length

Friction Slopes in HEC-RAS Average Conveyance (HEC-RAS default) - best results for all profile types (M 1, M 2, etc. ) Average Friction Slope - best results for M 1 profiles Geometric Mean Friction Slope used in USGS/FHWA WSPRO model Harmonic Mean Friction Slope best results for M 2 profiles In HECRAS, stand between sections and look half way up and down to the adjoining sections then average. In WSP 2, look downstream while standing at an upstream section. WSP 2 uses friction from upstream section for entire reach

Flow Classification Steep slope: normal depth below critical Mild slope: normal depth above critical

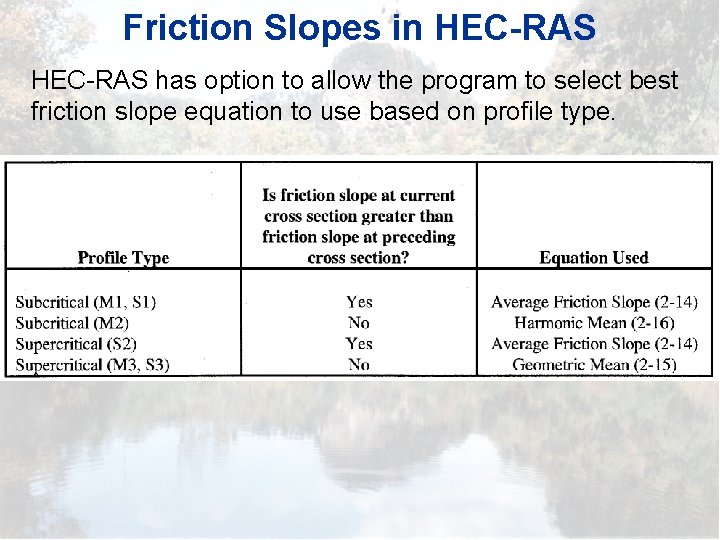
Friction Slopes in HEC-RAS has option to allow the program to select best friction slope equation to use based on profile type.

Other losses include: • Contraction losses • Expansion losses C = contraction or expansion coefficient

Contraction and Expansion Energy Loss Coefficients Note 1: WSP 2 uses the upstream section for the whole reach below it while HEC-RAS averages between the two X-sections. Note 2: WSP 2 only uses LSf in older versions and has added C to its latest version using the “LOSS” card.

Expansion and Contraction Coefficients • Contraction No transition loss Gradual transitions Typical bridge sections Abrupt transitions • Expansion 0. 0 0. 1 0. 3 0. 5 0. 6 0. 8 Notes: maximum values are 1. Losses due to expansion are usually much greater than contraction. Losses from short abrupt transitions are larger than those from gradual changes.

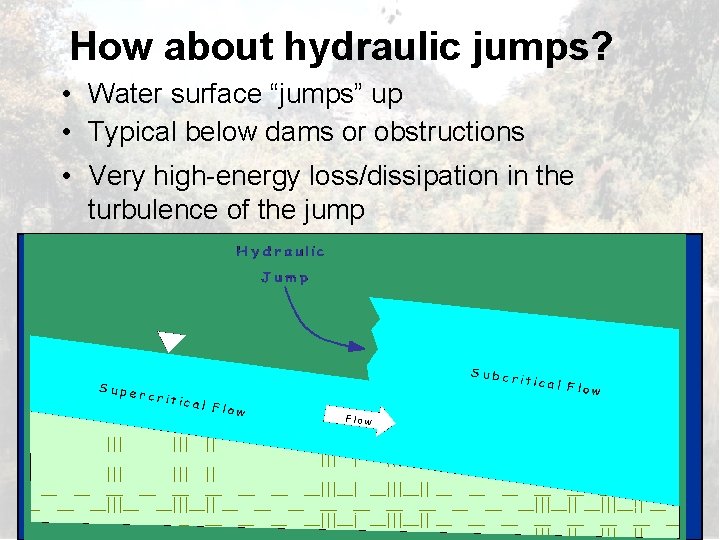
How about hydraulic jumps? • Water surface “jumps” up • Typical below dams or obstructions • Very high-energy loss/dissipation in the turbulence of the jump

A rapidly varying flow situation • Going from subcritical to supercritical flow, or vice-versa is considered a rapidly varying flow situation. • Energy equation is for gradually varied flow (would need to quantify internal energy losses) • Can use empirical equations • Can use momentum equation

Momentum Equation • Derived from Newton’s second law, F=ma • Apply F = ma to the body of water enclosed by the upstream and downstream x-sections. Difference in pressure + weight of water - external friction = mass x acceleration

Momentum Equation 2 ( V / 2 g ) + Y 2 +Z = 2 2 2 ( V / 2 g) + Y + Z + hm 1 1 1 The momentum and energy equations may be written similarly. Note that the loss term in the energy equation represents internal energy losses while the loss in the momentum equation (hm) represents losses due to external forces. In uniform flow, the internal and external losses are identical. In gradually varied flow, they are close.

HEC-RAS can use the Momentum Equation for • • Hydraulic jumps Hydraulic drops Low flow hydraulics at bridges Stream junctions. Since the transition is short, the external energy losses (due to friction) are assumed to be zero

When using HEC-RAS to model a 1 Dimensional steady flow situation, the modeler is assuming… • Flow is constant with respect to time (unsteady is an option but a different computational engine) • Flow is gradually varied with distance (except at structures where momentum or empirical equations are used) • Dominant flows in x direction (1 -D, because total energy head is assumed to be the same for all points in a cross section) • Channel slopes less than 1: 10 H (because pressure head is assumed to be represented by the water depth measured vertically. ) And the modeler is not concerned with • super elevation in bends • secondary currents

Unsteady Examples Natural streams are always unsteady - when can the unsteady component not be ignored? • Dam breach routing • Estuaries and Bays • Flood wave • others. . . Later in this class we will talk about this in more detail

Two Dimensional Examples • • Estuaries and bays Breach into a wide floodplain Junctions Others… Later in this class we will talk about this in more detail

Other assumptions in HEC-RAS • HEC-RAS is a fixed bed model – The cross section is static – Structures are fixed – HEC-6 (or HECRAS in sediment mode) allows for changes in the bed. • HEC-RAS can not by itself reflect upstream watershed changes. HEC-RAS is a simplification of the natural, chaotic system.

Q: What is an appropriate model approach to use? A: A normal depth assumption would be sufficient. At least in the reach that can be seen in this photo…

Q: What is an appropriate model approach to use? A: In these photos, we can see a confluence, variable section and a bridge. To model different design flows a steady flow, 1 -D approach would be good. Standard HECRAS would be suitable

Q: What is an appropriate model approach to use? Q 1 Q 2 Q 3 A: If the modeler in interested in flood heights below the dam at this dam discharge, a HECRAS steady, 1 D model could be used (if one knows the breach shape through the road). If the breach itself is to be modeled – then this is unsteady. If the modeler is interested in specifics of flooding through the water plant below the dam, it may be a 2 D situation. Above and through the dam is a reservoir routing condition. Q 1<Q 2=Q 3

The End You may need some help