Heating Ventilation and Air Conditioning Subject Code HVAC

Heating, Ventilation and Air Conditioning Subject Code: HVAC 1. 5 hr/Lecture for ten Lectures Location: H 10 Time: Wednesday, from 8: 30 – 10: 00 Instructor: Dr. Eng. M. S. Abd-Elhady (m. s. abdelhady@gmail. com) Office Hrs: Thursday till 5 PM Office no. : C 6. 106 2/10/2013 A/C Lecture 1 1

1. 5 hr/Lecture for ten Lectures Course Schedule Week Date Lecture Week Dat Lecture e 1: (28/9 - 3/10) 2/10 Lec. 1 8: (16 - 21/11) 2: (5 – 10/10) 9/10 Lec. 2 9: (23 – 28/11) 27/11 Lec. 7 10: (30/11 – 5/12) 4/12 Lec. 8 3: (12 – 17/10) Eed Alatha Mid-Term 4: (19 – 24/10) 23/10 Lec. 3 11: (7 – 12/12) 11/12 Lec. 9 5: (26 – 31/10) 30/10 Lec. 4 12: (14 – 19/12) 18/12 Lec. 10 6: (2 - 7/11) 6/11 Lec. 5 13: (21 – 26/12) Western Christmas 7: (9 – 14/11) 13/11 Lec. 6 14: (28 /12– 2/1) New Year’s day 2/10/2013 A/C Lecture 1 2

Engineering Thermodynamics The Lecturer: Dr. Eng. M. S. Abd-Elhady § BSc in Mech. Eng. , Energy Tech. , Ain-Shams Uni. , Egypt, 1993. § MSc in Mech. Eng. , Energy Tech. , Eindhoven Uni. of Technology, the Netherlands 1998. § Ph. D in Mech. Eng. , Energy Tech. , Eindhoven Uni. of Technology, the Netherlands 2005. § Associate Professor, Energy Tech. , Beni-Suief Uni. , Egypt 2011. 2/10/2013 A/C Lecture 1 3

Lecture Strategy Please 1 - Smile 2 - Respect the 2/10/2013 lecture time A/C Lecture 1 3 - make your 4 mobile Silent

Course Strategy Final Term exam Mid-Term exam Quizzes Assignments Project 2/10/2013 : 40 % : 25 % : 10 % A/C Lecture 1 5

Textbooks - References 1 - Yunus A. Cengel and Michael A. Boles, “Thermodynamics: An Engineering Approach, ” 6 th edition, Mc. Graw Hill, 2008. 2 - Arora C. P. , “Refrigeration and Air Conditioning”, 2 nd edition, Mc. Graw Hill, 2000. 2/10/2013 A/C Lecture 1 6

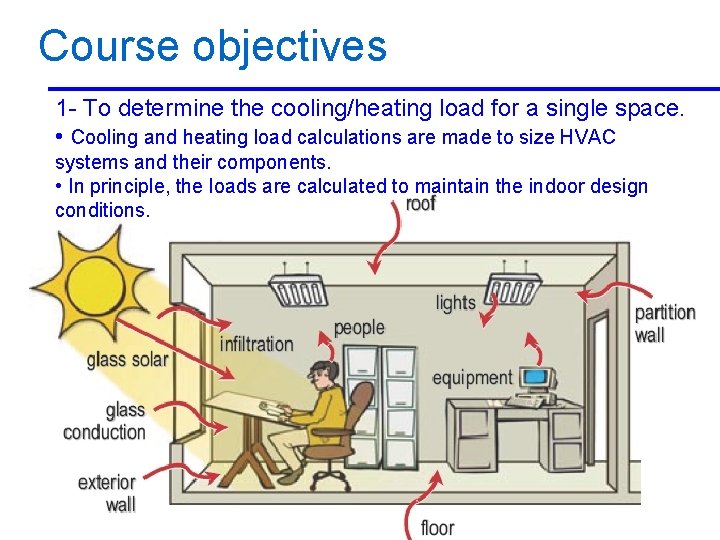
Course objectives 1 - To determine the cooling/heating load for a single space. • Cooling and heating load calculations are made to size HVAC systems and their components. • In principle, the loads are calculated to maintain the indoor design conditions. 2/10/2013 A/C Lecture 1 7

Course objectives 2 - To determine the different components of a cooling load. Analysis of this breakup provides an idea of how much each component of the building envelope contributes to the overall cooling load and what can be done to reduce this load. Reducing solar heat gain through windows is clearly one of the key areas. 2/10/2013 A/C Lecture 1 8

Course objectives 3 - Design an efficient and effective air conditioning system. • Machine selection and air distribution. 4 - Proper design, installation, and operation of the control of an HVAC system. HVAC control is an important factor in achieving the desired performance of an HVAC system. In general, automatic control can: a- Satisfy occupant comfort demands. b- Bolster occupant productivity. c- Minimize system energy consumption. d- Work effectively with other building systems. 2/10/2013 A/C Lecture 1 9

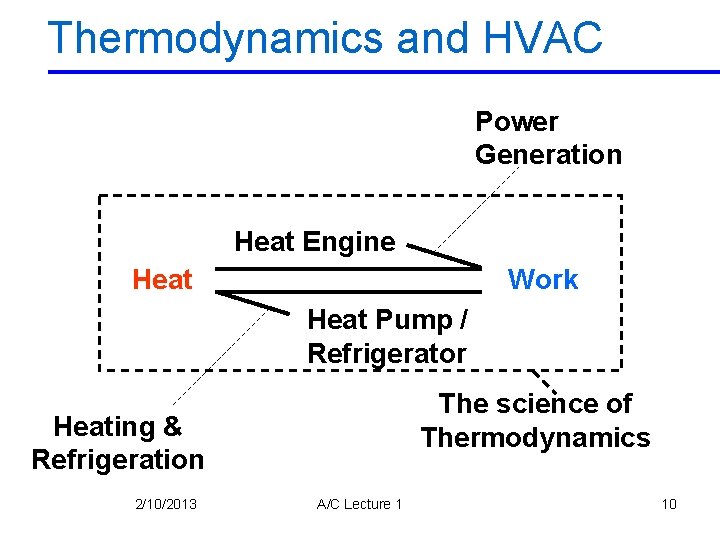
Thermodynamics and HVAC Power Generation Heat Engine Work Heat Pump / Refrigerator The science of Thermodynamics Heating & Refrigeration 2/10/2013 A/C Lecture 1 10

• Two important areas of application for THERMODYNAMICS are: 1. Power Generation Airconditioning Engineer 2. Refrigeration 2/10/2013 Power/Thermal Engineer A/C Lecture 1 11

Meaning of Air-Conditioning Six - Control: 1 - Control of air temperature by heating or cooling 2 - Control of air humidity By humidification of dehumidification 3 - Control of air cleanliness By filtration, the filtration efficiency can vary from 0. 5 % to 99. 999 % depending on the application. 4 - Control of air fresheness By ventilation 2/10/2013 A/C Lecture 1 12

Meaning of Air-Conditioning Six - Control: 5 - Control of air motion By air distribution 6 - Control of noise By using accustic instulators and controling the air speed. In our design we aim at an optimium design and not the best design 2/10/2013 13 Over design is a wrong design A/C Lecture 1

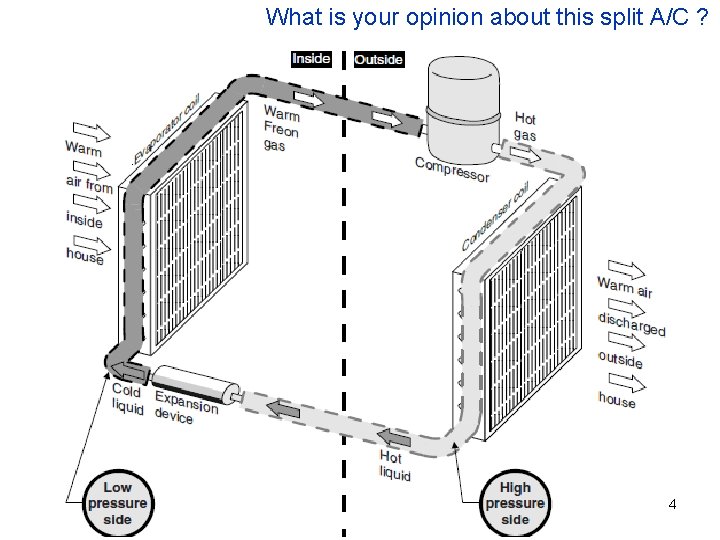
What is your opinion about this split A/C ? 2/10/2013 A/C Lecture 1 14

What is your opinion about this split A/C ? Indoor Unit Outdoor Unit 2/10/2013 A/C Lecture 1 15

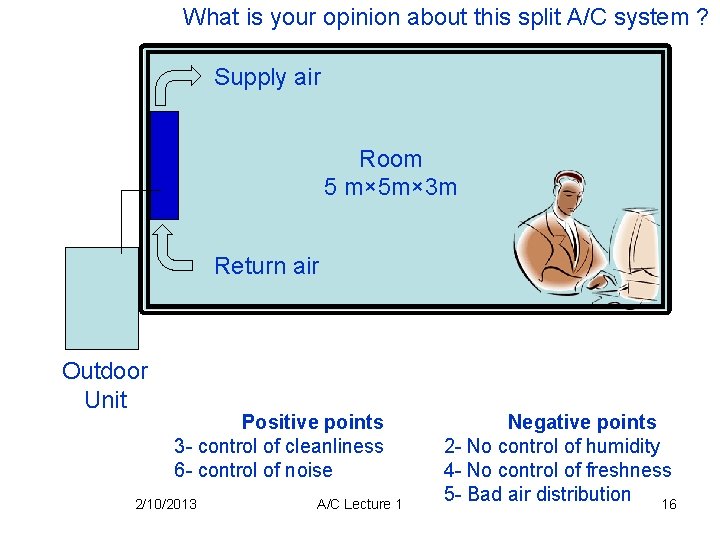
What is your opinion about this split A/C system ? Supply air Room 5 m× 5 m× 3 m Return air Outdoor Unit Positive points 3 - control of cleanliness 6 - control of noise 2/10/2013 A/C Lecture 1 Negative points 2 - No control of humidity 4 - No control of freshness 5 - Bad air distribution 16

Lecture 1 Refrigerating Machine and the Reversed Carnot Cycle 2/10/2013 A/C Lecture 1 17

Objectives 1 - Introduce the concepts of refrigerators and heat pumps and the measure of their performance. 2 - Analyze the ideal vapor-compression refrigeration cycle. 2/10/2013 A/C Lecture 1 18

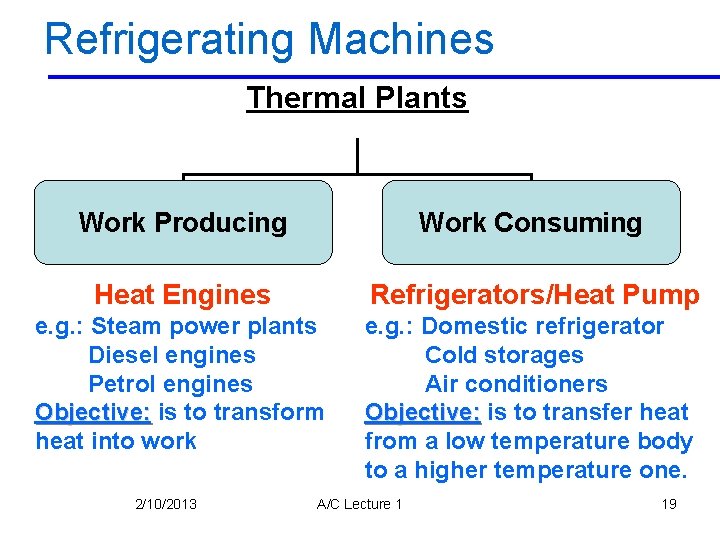
Refrigerating Machines Thermal Plants Work Producing Work Consuming Heat Engines Refrigerators/Heat Pump e. g. : Steam power plants Diesel engines Petrol engines Objective: is to transform heat into work e. g. : Domestic refrigerator Cold storages Air conditioners Objective: is to transfer heat from a low temperature body to a higher temperature one. 2/10/2013 A/C Lecture 1 19

There are essentially two categories of thermal plants (i) Heat engines or work producing plants (ii) Refrigeration/heat pump plants or work consuming plants. • The devices or systems used to produce a net power output are often called engines, engines and thermodynamic cycles they operate on are called power cycles • The devices or systems used to produce a refrigeration effect are called refrigerators, air conditioners, or heat pumps, pumps and the cycles they operate on are called refrigeration cycles 2/10/2013 A/C Lecture 1 20

Pure substance • A substance that has a fixed chemical composition throughout is called a pure substance. Ex. : Water, nitrogen, helium, and carbon dioxide. • A pure substance does not have to be of a single chemical element or compound. However, a mixture of various chemical elements or compounds also qualifies as a pure substance as long as the mixture is homogeneous. Ex. Air. 2/10/2013 A/C Lecture 1 21

Pure substance • A mixture of two or more phases of a pure substance is still a pure substance as long as the chemical composition of all phases is the same. Ex. A mixture of liquid and gaseous water. 2/10/2013 A/C Lecture 1 22

A pure substance exists in different phases depending on its energy level. • In the liquid phase, a substance that is not about to vaporize is called a compressed or sub-cooled liquid. • The liquid during vaporization is called saturated liquid Subcooled 2/10/2013 water A/C Lecture 1 Saturated waterwater vapor 23

2/10/2013 A/C Lecture 1 24

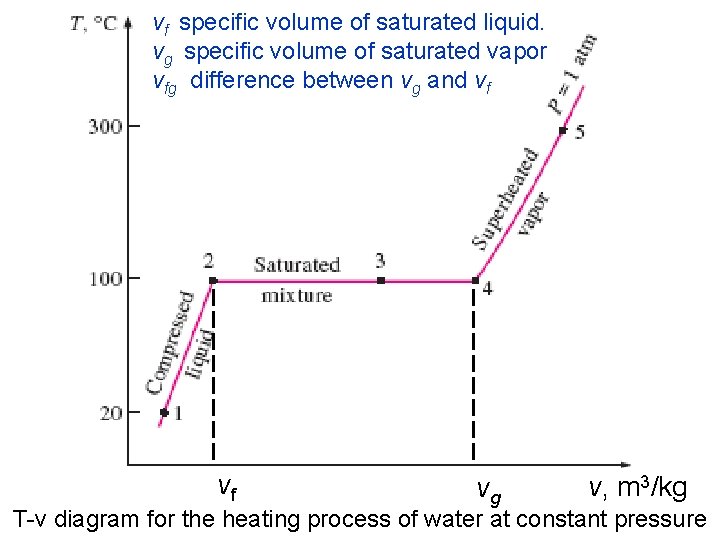
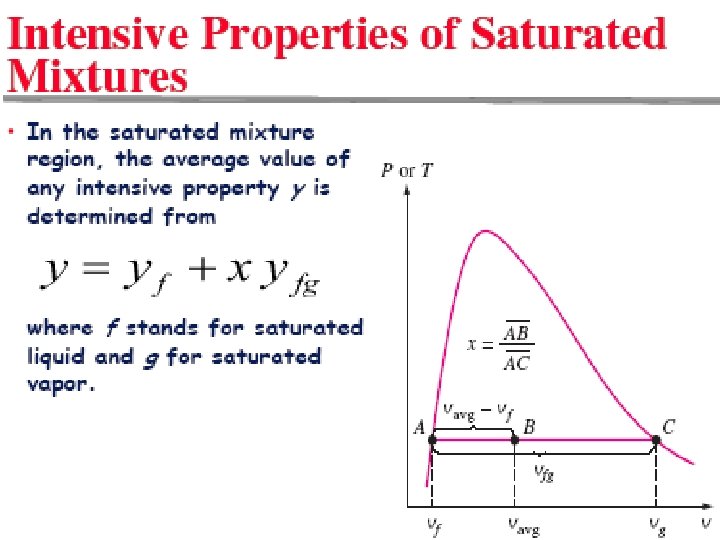
vf specific volume of saturated liquid. vg specific volume of saturated vapor vfg difference between vg and vf 2/10/2013 vf A/C Lecture 1 vg v, m 3/kg 25 T-v diagram for the heating process of water at constant pressure

Phase-change process During a phase-change process. • The temperature and pressure of a pure substance are dependent properties. • At a given pressure, a substance changes phase at a fixed temperature called the saturation temperature. • At a given temperature, a substance changes phase at a fixed pressure called the saturation pressure. • During a boiling process, both the liquid and vapor phases co-exist in equilibrium, and under this condition: 1 - The liquid is called saturated liquid. 2 - The vapor is called saturated vapor. 2/10/2013 A/C Lecture 1 26

Phase-change process The statement “water boils at 100°C” is incorrect The correct statement is “water boils at 100°C at 1 atm pressure. ” pressure The only reason water starts boiling at 100°C is the pressure is kept constant at 1 atm (101. 325 k. Pa). If the pressure inside the cylinder is raised to 500 k. Pa by adding weights on top of the piston, water would start boiling at 151. 8°C P=500 k. Pa T= 151. 8 ºC 2/10/2013 A/C Lecture 1 27

Example: • Calculate the boiling temperature for water in a steam boiler if the operating pressure is kept constant at 1 MPa. Solution: From table A-5, the saturation temperature that corresponds to a saturation pressure 1 MPa is 179. 88 ºC 2/10/2013 A/C Lecture 1 28

T-v diagram of constantpressure phase-change processes of a pure substance at various pressures 295 ºC 100 ºC 2/10/2013 A/C Lecture 1 29

• The saturated liquid states in the above Fig. can be connected by a line called the saturated liquid line • The saturated vapor states in the same figure can be connected by another line, called the saturated vapor line These two lines meet at the critical point, point forming a dome. • All the compressed liquid states are located in the region to the left of the saturated liquid line, called the compressed liquid region. • All the superheated vapor states are located to the right of the saturated vapor line, called the A/C Lecture 1 superheated vapor region. 2/10/2013 30

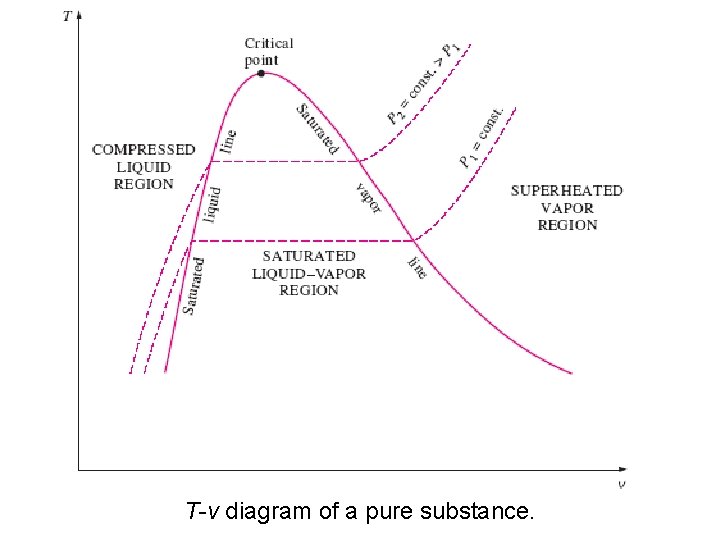
2/10/2013 1 T-v diagram A/C of Lecture a pure substance. 31

• All the states that involve both phases in equilibrium are located under the dome, called the saturated liquid–vapor mixture region, or the wet region. • All states that are above the dome, are a single phase state. • The critical point is defined as the point at which the saturated liquid and saturated vapor states are identical. 2/10/2013 A/C Lecture 1 32

The P-v Diagram • The general shape of the P-v diagram of a pure substance is very much like the T-v diagram. • T constant lines on this diagram have a downward trend, as shown in the Figure below. 2/10/2013 A/C Lecture 1 33

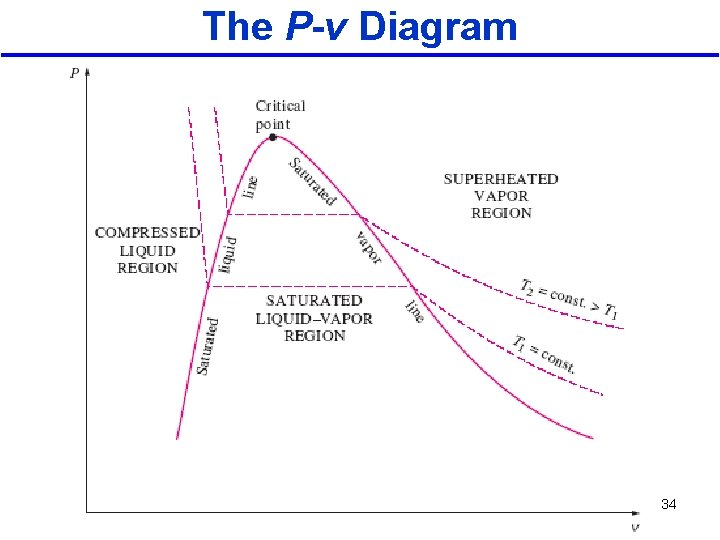
The P-v Diagram 2/10/2013 A/C Lecture 1 34

PROPERTY TABLES • Some thermodynamic properties can be measured easily. • Other properties are calculated using the relations between them and the measurable properties. • The results of these measurements and calculations are presented in property tables in a convenient format, e. g. water tables as follows; TABLE A– 4: Saturated water—Temperature table. TABLE A– 5: Saturated water—Pressure table. TABLE A– 6: Superheated water. TABLE A– 7: Compressed liquid water. 2/10/2013 A/C Lecture 1 35

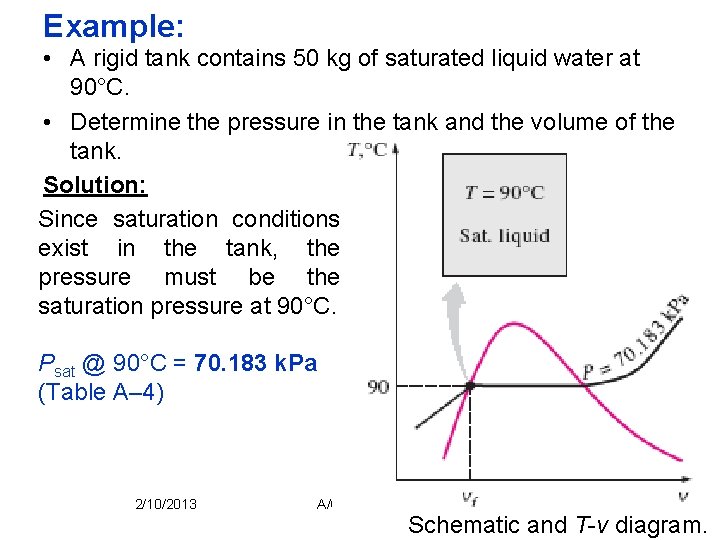
Example: • A rigid tank contains 50 kg of saturated liquid water at 90°C. • Determine the pressure in the tank and the volume of the tank. Solution: Since saturation conditions exist in the tank, the pressure must be the saturation pressure at 90°C. Psat @ 90°C = 70. 183 k. Pa (Table A– 4) 2/10/2013 A/C Lecture 1 36 Schematic and T-v diagram.

• The specific volume of the saturated liquid at 90°C is vf @ 90°C is 0. 001036 m 3/kg (Table A– 4) • Then the total volume V of the tank becomes V = mv = 50 kg x 0. 001036 m 3/kg = 0. 0518 m 3 2/10/2013 A/C Lecture 1 37

Example: • A mass of 200 g of saturated liquid water is completely vaporized at a constant pressure of 100 k. Pa. • Determine (a) the volume change and • (b) the amount of energy transferred to the water. Solution: a) The volume change per unit mass during a vaporization process is vfg, which is the difference between vg and vf. Reading these values from Table A– 5 at 100 k. Pa and substituting yield 2/10/2013 A/C Lecture 1 38 Schematic and T-v diagram.

2/10/2013 A/C Lecture 1 39

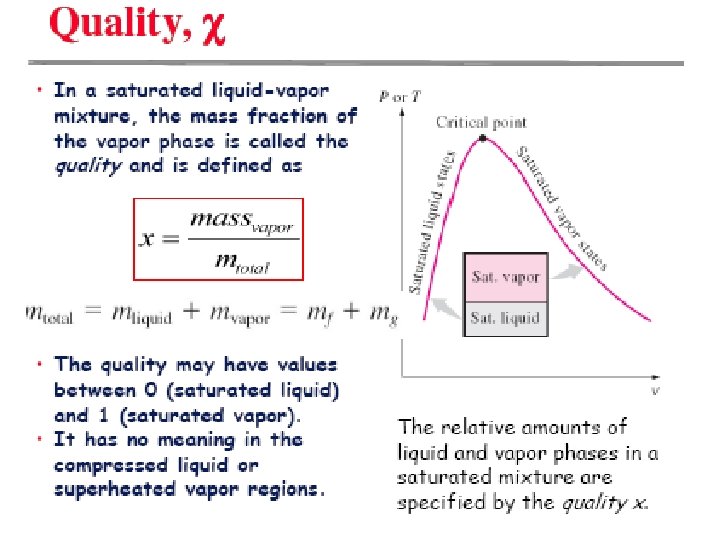
2/10/2013 A/C Lecture 1 40

2/10/2013 A/C Lecture 1 41

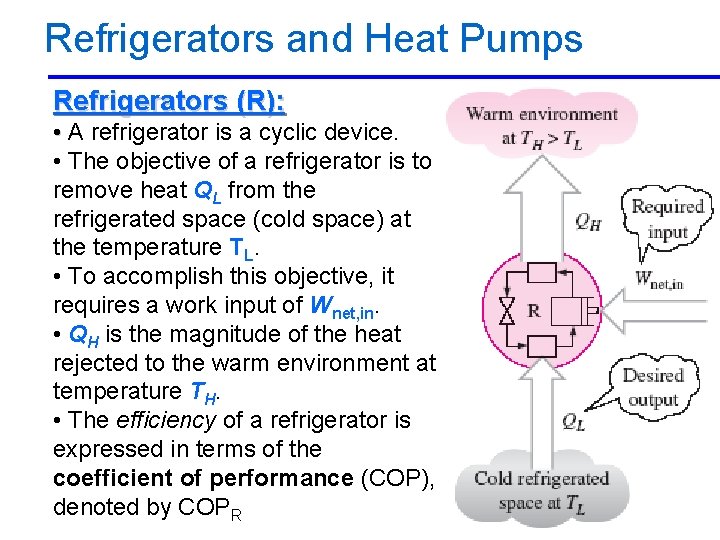
Refrigerators and Heat Pumps Refrigerators (R): • A refrigerator is a cyclic device. • The objective of a refrigerator is to remove heat QL from the refrigerated space (cold space) at the temperature TL. • To accomplish this objective, it requires a work input of Wnet, in. • QH is the magnitude of the heat rejected to the warm environment at temperature TH. • The efficiency of a refrigerator is expressed in terms of the coefficient of performance (COP), A/C Lecture 1 denoted 2/10/2013 by COPR 42

Refrigerators and Heat Pumps Refrigerators (R): • The coefficient of performance The conservation of energy principle for a cyclic device requires that Wnet, in=QH-QL Then the COP relation can be expressed as 2/10/2013 A/C Lecture 1 43

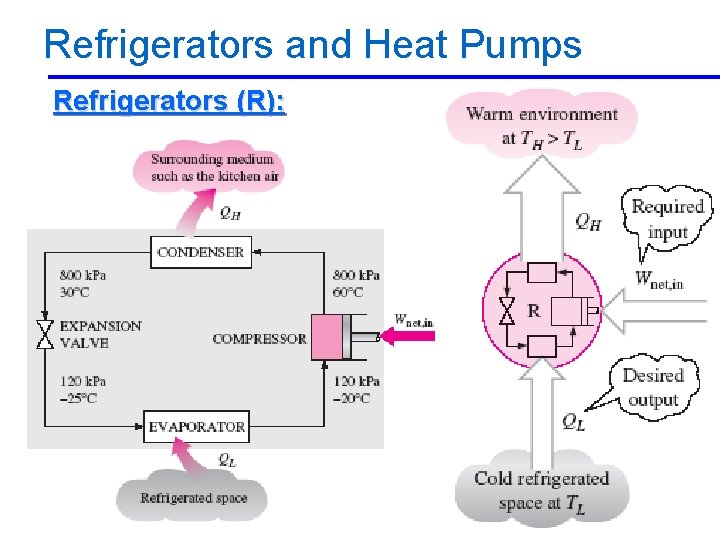
Refrigerators and Heat Pumps Refrigerators (R): 2/10/2013 A/C Lecture 1 44

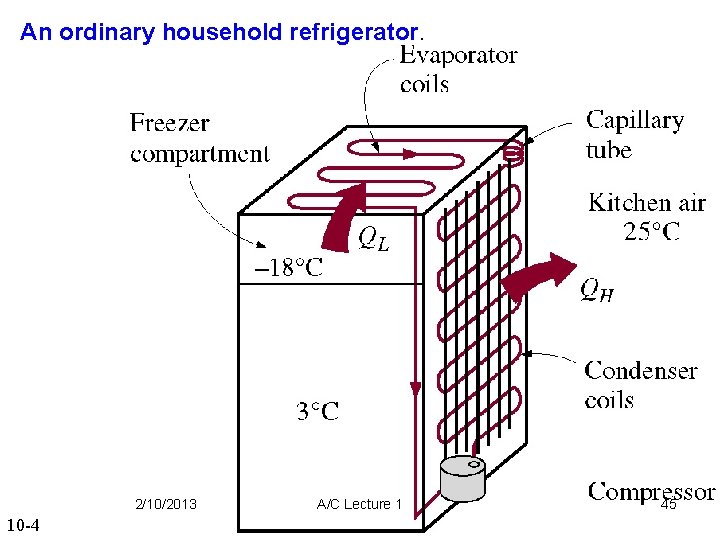
An ordinary household refrigerator. 2/10/2013 10 -4 A/C Lecture 1 45

Schematic and T-s diagram for the ideal vapor-compression refrigeration cycle. 31. 33 -18. 8 2/10/2013 A/C Lecture 1 46

Example A refrigerator uses R-134 a as the working fluid and operates on an ideal vapor-compression refrigeration cycle between 0. 14 and 0. 9 MPa. If the mass flow rate of the refrigerant is 0. 05 kg/s, determine: (a) the rate of heat removal from the refrigerated space and the power input to the compressor, (b) the rate of heat rejection to the environment, and (c) the COP of the refrigerator. 2/10/2013 A/C Lecture 1 47

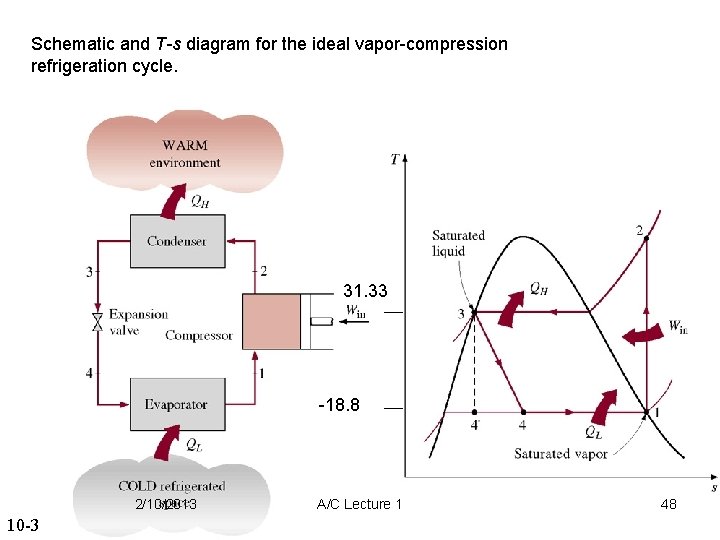
Schematic and T-s diagram for the ideal vapor-compression refrigeration cycle. 31. 33 -18. 8 2/10/2013 10 -3 A/C Lecture 1 48

Ex 10 -1 Refrigeration Cycle P 3 = 0. 80 MPa T 3 = 31. 33 o. C h 3 = 93. 42 k. J/kg s 3 = 0. 3459 k. J/(kg K) P 4 = 0. 14 k. Pa T 4 = -18. 80 o. C x 3 = 0 P 2 = 0. 80 MPa s 1 = 0. 9322 T 2 = 31. 68 h 2 = 272. 05 P 1 = 0. 14 MPa T 1 = -18. 80 o. C x 1 = 1. 0 h 4 = 93. 42 s 1 = 0. 9322 x 4 = 0. 322 s 4 = 0. 3717 h 1 = 236. 04 2/10/2013 A/C Lecture 1 49

Condenser <2 -3> 2/10/2013 A/C Lecture 1 50

Compressor <1 -2> 2/10/2013 A/C Lecture 1 51

Evaporator <4 -1> 2/10/2013 A/C Lecture 1 52

Refrigeration System 2/10/2013 A/C Lecture 1 53

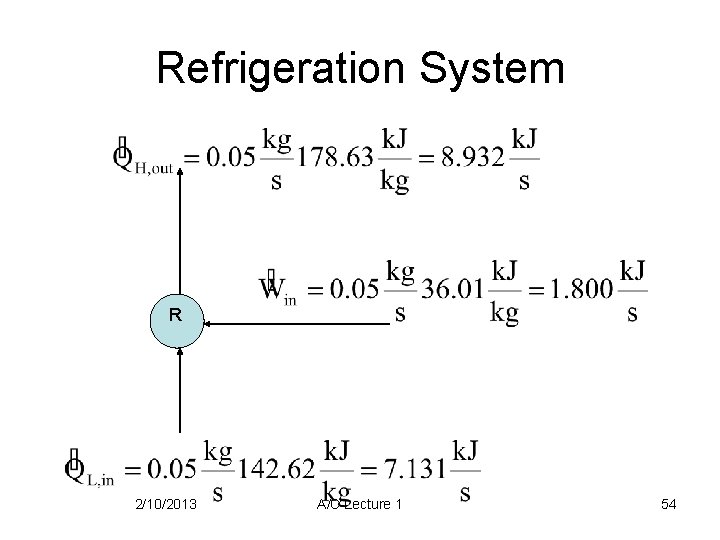
Refrigeration System R 2/10/2013 A/C Lecture 1 54

Refrigerators and Heat Pumps Heat Pump (HP): • Refrigerators and heat pumps operate on the same cycle but differ in their objectives. • The objective of a heat pump, however, is to maintain a heated space at a high temperature. • The efficiency of a Heat pump is also expressed in terms of the coefficient of performance (COP), denoted by COPHP 2/10/2013 A/C Lecture 1 55

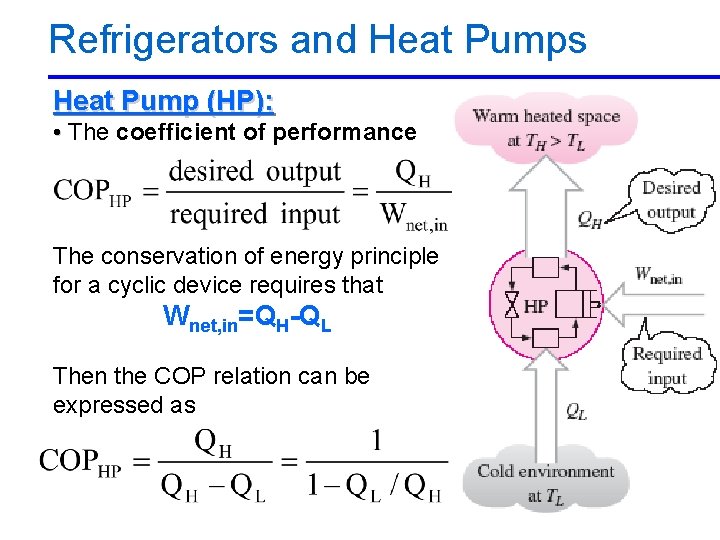
Refrigerators and Heat Pumps Heat Pump (HP): • The coefficient of performance The conservation of energy principle for a cyclic device requires that Wnet, in=QH-QL Then the COP relation can be expressed as 2/10/2013 A/C Lecture 1 56

• The value of COPR can be greater than unity. • One reason for expressing the efficiency of a refrigerator by another term—the coefficient of performance—is the performance desire to avoid the oddity of having efficiencies greater than unity. When installed backward, an air 2/10/2013 conditioner functions A/C Lectureas 1 a heat pump. 57

Example: Heat Pumps A heat pump is used to meet the heating requirements of a house and maintain it at 20°C. On a day when the outdoor air temperature drops to 2°C, the house is estimated to lose heat at a rate of 80, 000 k. J/h. If the heat pump under these conditions has a COP of 2. 5, Determine: (a) the power consumed by the heat pump, (b) the electrical energy consumed per month, the electrical bill if the electricity price is 0. 1 $/k. Wh, and (c) the extra money has to be paid monthly, if the electrical heaters are used. Solution: a) The power consumed by this heat pump is determined from the definition of the coefficient of performance to be 2/10/2013 A/C Lecture 1 58

Example: Heat Pumps (b) Electrical energy. consumed per month = W × 30 day/month× 24 h/day = 8. 9 k. W × 720 h/month = 6408 k. Wh/month Electricity bill/month = 6408 k. Wh × 0. 1 $/k. Wh = 640 $ (c) The electrical heater has to supply heat equal to QH Assuming that the heating efficiency of the electrical heater is 100 % Therefore the Electrical. energy consumed per month = QH × 30 day/month× 24 h/day = 22. 22 × 720 h/month = 16000 k. Wh/month Electricity bill/month = 16000 k. Wh × 0. 1 $/k. Wh = 1600 $ 2/10/2013 A/C Lecture 1 59

The Carnot Refrigerator & Heat Pump • A refrigerator or a heat pump that operates on the reversed Carnot cycle is called a Carnot refrigerator, or a Carnot heat pump. • The reversed Carnot cycle is the most efficient refrigeration cycle operating between two specific temperature levels • The Carnot cycle is a reversible cycle and it consists of: a- two isothermal processes and b- two isentropic porcesses as follows: 2/10/2013 A/C Lecture 1 60

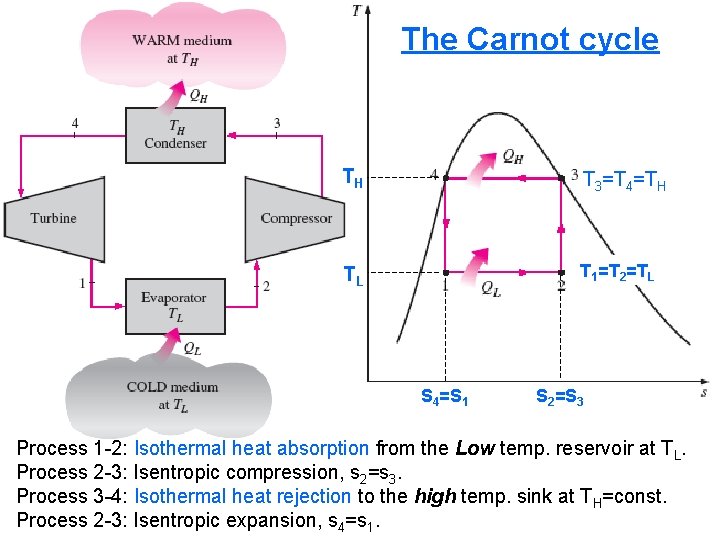
The Carnot cycle TH T 3=T 4=TH TL T 1=T 2=TL S 4=S 1 S 2=S 3 Process 1 -2: Isothermal heat absorption from the Low temp. reservoir at TL. Process 2 -3: Isentropic compression, s 2=s 3. Process 3 -4: Isothermal heat rejection to the 2/10/2013 A/C Lecture 1 high temp. sink at TH=const. 61 Process 2 -3: Isentropic expansion, s 4=s 1.

The coefficient of performance of any refrigerator or heat pump, reversible or irreversible, is equal to and Where: QL is the amount of heat absorbed from the low-temperature medium QH is the amount of heat rejected to the high-temperature medium. However for a reversible Carnot refrigerator or heat pump QL =TL(S 2 -S 1) and QH =TH(S 3 -S 4)=TH(S 2 -S 1) Then the COP relations for reversible refrigerators and heat pumps become and These are the highest coefficients of performance that a refrigerator or a heat pump operating between the temperature limits of TL and TH can have. 2/10/2013 or heat pumps A/C Lecture 1 62 All actual refrigerators operating between these temperature limits (TL and TH) have lower coefficients of performance.

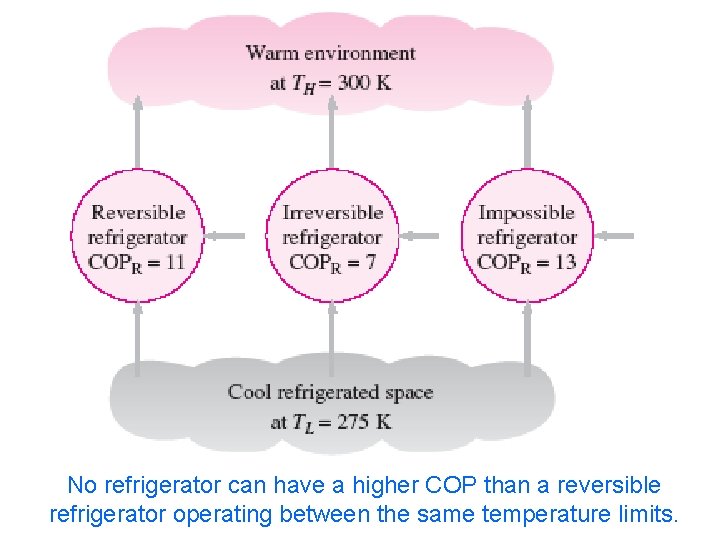
No refrigerator can have a higher COP than a reversible 2/10/2013 A/C Lecture 1 63 refrigerator operating between the same temperature limits.

The coefficients of performance of actual COPR and reversible COPR, rev refrigerator operating between the same temperature limits can be compared as follows: 2/10/2013 A/C Lecture 1 64

Example: An inventor claims to have developed a refrigerator that maintains the refrigerated space at 2°C while operating in a room where the temperature is 25°C and that has a COPR of 13. 5. Is this claim reasonable? Solution: The performance of this refrigerator can be evaluated by comparing it with a reversible refrigerator operating between the same temperature limits: This is the highest COP a refrigerator can have when absorbing heat from a cool medium at 2°C and rejecting it to a warmer medium at 25°C. Since the COP claimed by the inventor is above this maximum value, therefore 2/10/2013 the claim is false. A/C Lecture 1 at TH=25 o. C at TL=2 o. C 65

Vapor as a Refrigerant in Reversed Carnot Cycle The Carnot cycle Condensation TH T 3=T 4=TH Expansion Compression T 1=T 2=TL TL Evaporation S 4=S 1 2/10/2013 S 2=S 3 A/C Lecture 1 66

Vapor as a Refrigerant in Reversed Carnot Cycle The thermodynamic analysis per unit mass of the rerrfigerant, for the four flow processes of the cycle , using already steady flow energy equations as follows: Refrigeration effect, q. L=h 2 -h 1 [k. J/kg] Heat rejected, |q. H|=h 3 -h 4 [k. J/kg] Compressor work, |wc|=h 3 -h 2 [k. J/kg] Expansion work, we=h 4 -h 1 [k. J/kg] Net work = |wnet| = |wc|-we= h 3 - h 2 - (h 4 -h 1) = |q. H|-q. L= h 3 - h 4 - (h 2 -h 1) COP= 2/10/2013 A/C Lecture 1 67

Example A carnot refrigerator has working temperatures of -30 o. C and 35 o. C. If it operates with R 12 as working substance, calculate the work of isentropic compression and that of isentropic expansion, and refrigeration effect, heat rejected per kg of the refrigerant and the COP of the cycle. 2/10/2013 A/C Lecture 1 68

Example A carnot refrigerator has working temperatures of -30 o. C and 35 o. C. If it operates with R 12 as working substance, calculate the work of isentropic compression and that of isentropic expansion, and refrigeration effect, heat rejected per kg of the refrigerant and the COP of the cycle. Solution: From the table of properties of R 12, we have: s 2=s 3=0. 6839 k. J/kg. K sf 1=sf 2=0. 0371 k. J/kg. K s 4=s 1=0. 2559 k. J/kg. K sg 1=sf 2=0. 7171 k. J/kg. K h 3=201. 5 k. J/kg hf 1=hf 2=8. 9 k. J/kg h 4=69. 5 k. J/kg hg 2=hf 2=174. 2 k. J/kg Hence, by putting s 2=s 3 and s 1=s 4, we get the dryness factions at states 1 and 2 as 2/10/2013 A/C Lecture 1 69

Enthalpies at states 2 and 1 Refrigeration effect, q. L = h 2 - h 1 = 166 - 62. 1 = 103. 9 k. J/kg Heat rejected, |q. H| = h 3 – h 4 = 201. 5 - 69. 5 = 132 k. J/kg Compressor work, |wc| = h 3 - h 2 = 201. 5 - 166 = 35. 5 k. J/kg Expansion work, we = h 4 – h 1 = 69. 5 - 62. 1 = 7. 4 k. J/kg Net work = |wnet| = |wc|-we= 35. 5 - 7. 4 = 28. 1 k. J/kg = |q. H|-q. L= 132 – 103. 9 = 28. 1 k. J/kg COP= q. L/wnet=103. 9/28. 1=3. 74 2/10/2013 A/C Lecture 1 70

Thanks for your attention