Heat Transfer Problems 12 4 Case 1 Silver

Heat Transfer Problems

12 -4 – Case #1 Silver Spoon Steel Spoon m = 10. 0 g Ti = 25. 0 o. C s = 0. 233 J/ g o. C s = 0. 51 J/ g o. C Boiling Water Baths at 100 o. C

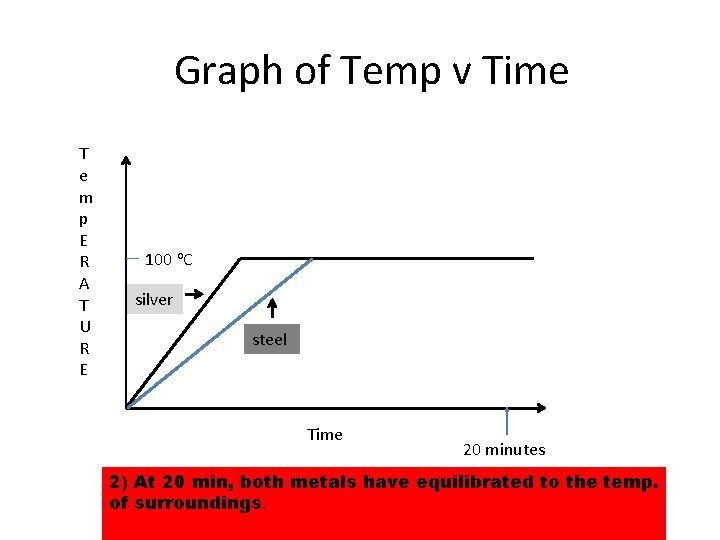
Graph of Temp v Time T e m p E R A T U R E 100 o. C silver steel Time 20 minutes 2) At 20 min, both metals have equilibrated to the temp. of surroundings.

3) Which Spoon’s atom’s have a greater average kinetic energy? Temperature is directly proportional to average kinetic energy. BOTH ARE AT SAME TEMPERATURE THUS KINETIC ENERGIES ARE THE SAME.

HW 12 -4 #4) Which spoon has more stored heat Q? • Steel. It takes 0. 51 J to raise the temp. of 1 g of Steel by 1 o. C. It takes only. 23 J of energy to raise the temperature of 1 g of silver by 1 o. C.

4) Calculate Q absorbed after 20 min. TF = 100 o. C of spoons; • Q = sm∆T • Silver: • Q = (0. 23 J/g o. C)(10. 0 g) (100 o. C – 25 o. C) • Q = 172. 5 = 170 J (2 SF) • Steel: • Q = (0. 51 J/g o. C)(10. 0 g) (100 o. C – 25 o. C) • Q = 382. 5 = 380 J (2 SF)

Case 2 – If two objects absorb the exact same amount of heat energy in joules, will they be at same final temperature? • Q = sm∆T ; ∆T = Q/ sm; ∆T = Tf – Ti; Tf = ∆T + Ti Silver • ∆T = 1000. J (0. 23 J/ g o. C)( 10. 0 g) =434. 7= 430 (2 SF) Tf = ∆T + Ti; Tf = 430 + 25 = 455 o. C Steel: ∆T = 1000. J (0. 51 J/g o. C) (10. 0 g) = 196 = 200 (2 SF) Tf = ∆T + Ti; Tf = 200 + 25 = 225 o. C Different s values causes different ∆T

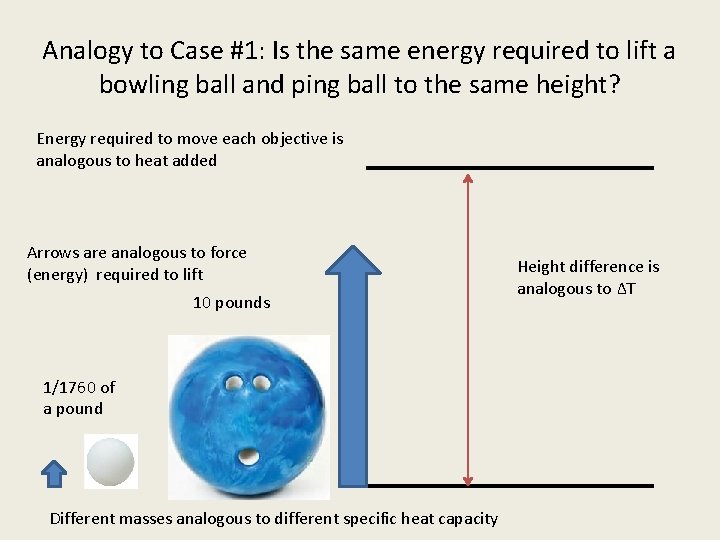
Analogy to Case #1: Is the same energy required to lift a bowling ball and ping ball to the same height? Energy required to move each objective is analogous to heat added Arrows are analogous to force (energy) required to lift 10 pounds 1/1760 of a pound Different masses analogous to different specific heat capacity Height difference is analogous to ∆T

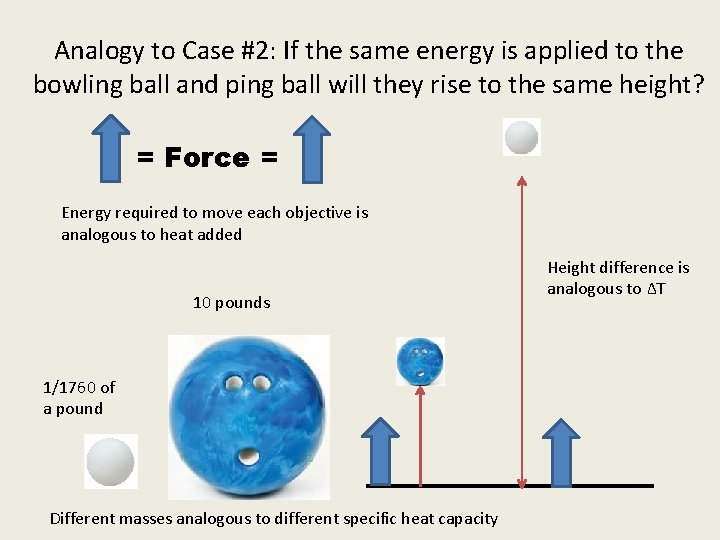
Analogy to Case #2: If the same energy is applied to the bowling ball and ping ball will they rise to the same height? = Force = Energy required to move each objective is analogous to heat added 10 pounds 1/1760 of a pound Different masses analogous to different specific heat capacity Height difference is analogous to ∆T