Heat Transfer Mechanisms Dr AA Department of Chemical

Heat Transfer Mechanisms Dr. AA Department of Chemical Engineering University Teknology Malaysia

Conduction Dr. AA Department of Chemical Engineering University Teknology Malaysia

Heat Conduction Key Question: How does heat pass through different materials?

Heat Transfer • The science of how heat flows is called heat transfer. • There are three ways heat transfer works: conduction, convection, and radiation. • Heat flow depends on the temperature difference.

Thermal Equilibrium • Two bodies are in thermal equilibrium with each other when they have the same temperature. • In nature, heat always flows from hot to cold until thermal equilibrium is reached.

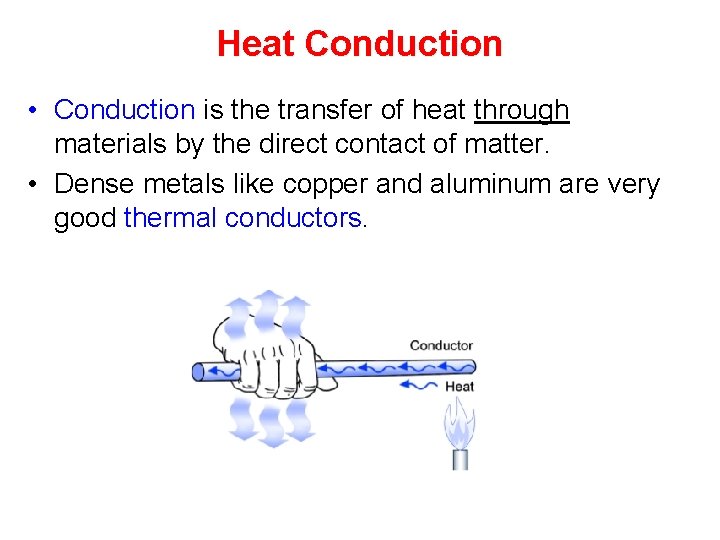
Heat Conduction • Conduction is the transfer of heat through materials by the direct contact of matter. • Dense metals like copper and aluminum are very good thermal conductors.

Heat Conduction • A thermal insulator is a material that conducts heat poorly. • Heat flows very slowly through the plastic so that the temperature of your hand does not rise very much.

Heat Conduction • The ability to conduct heat often depends more on the structure of a material than on the material itself. – Solid glass is a thermal conductor when it is formed into a beaker or cup. – When glass is spun into fine fibers, the trapped air makes a thermal insulator.

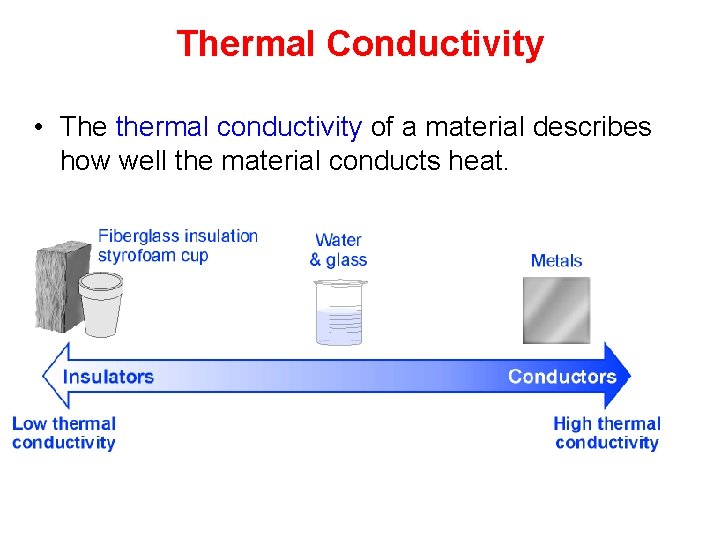
Thermal Conductivity • The thermal conductivity of a material describes how well the material conducts heat.

Thermal Conductivity • Heat conduction in solids and liquids works by transferring energy through bonds between atoms or molecules.

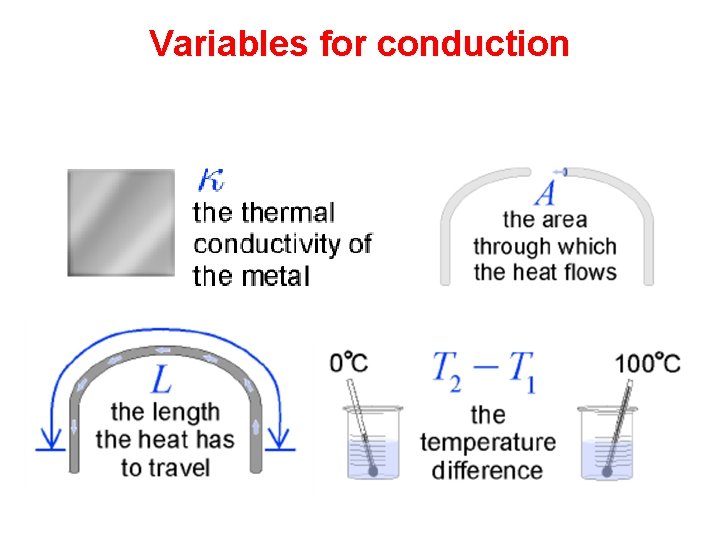
Heat Conduction Equation Thermal conductivity (watts/mo. C) Heat flow (watts) Area of cross section (m 2) PH = k A (T 2 -T 1) L Temperature difference (o. C) Length (m)

Variables for conduction

Convection Dr. AA Department of Chemical Engineering University Teknology Malaysia

Convection Key Question: Can moving matter carry thermal energy?

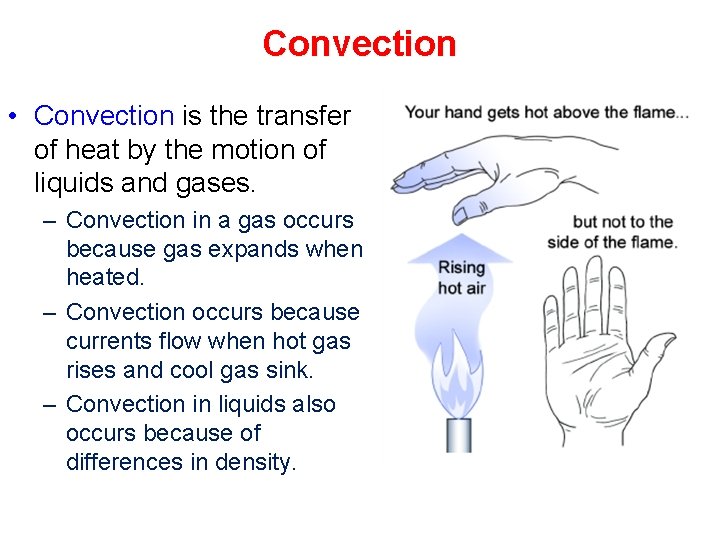
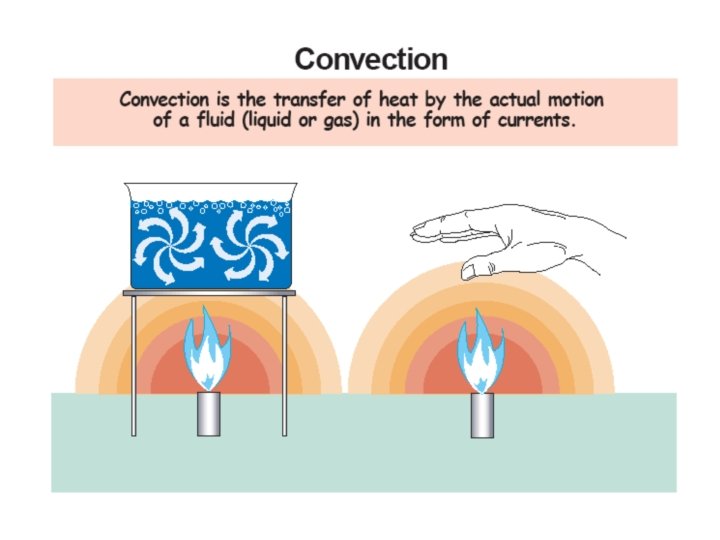
Convection • Convection is the transfer of heat by the motion of liquids and gases. – Convection in a gas occurs because gas expands when heated. – Convection occurs because currents flow when hot gas rises and cool gas sink. – Convection in liquids also occurs because of differences in density.

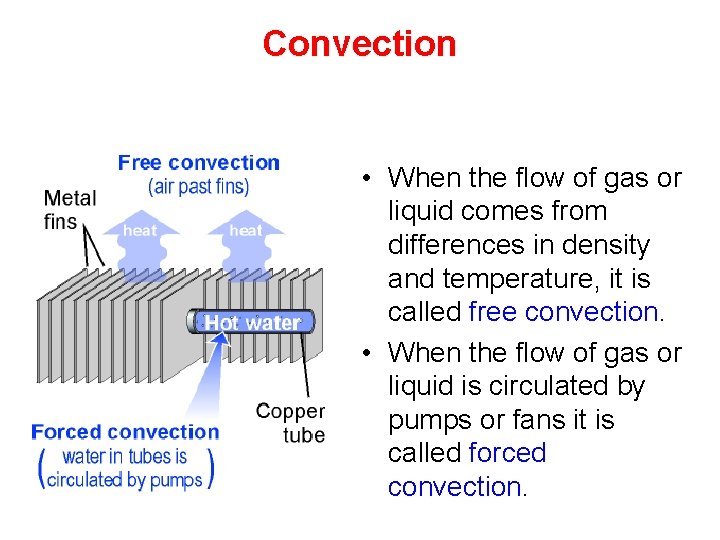
Convection • When the flow of gas or liquid comes from differences in density and temperature, it is called free convection. • When the flow of gas or liquid is circulated by pumps or fans it is called forced convection.

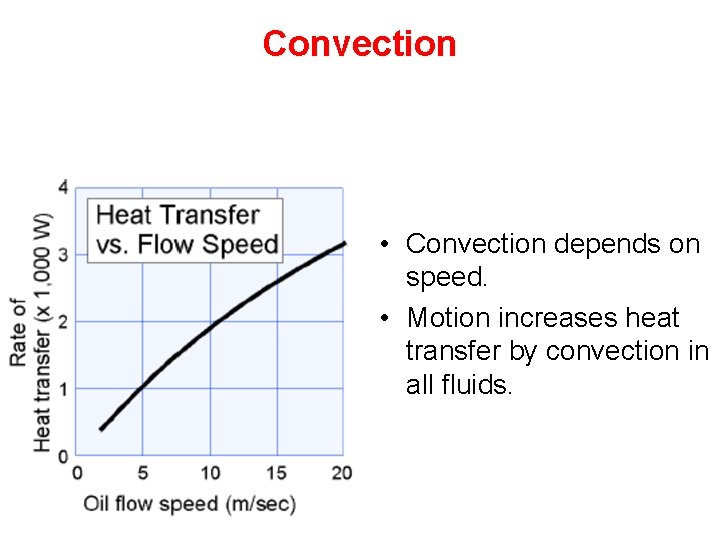
Convection • Convection depends on speed. • Motion increases heat transfer by convection in all fluids.

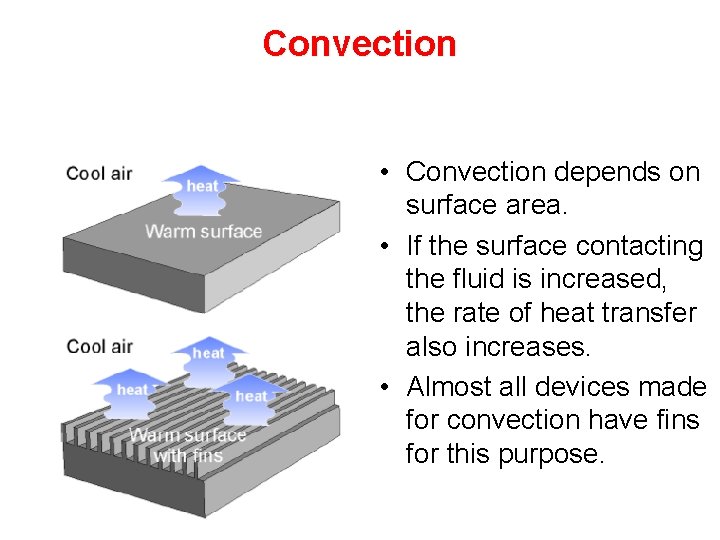
Convection • Convection depends on surface area. • If the surface contacting the fluid is increased, the rate of heat transfer also increases. • Almost all devices made for convection have fins for this purpose.

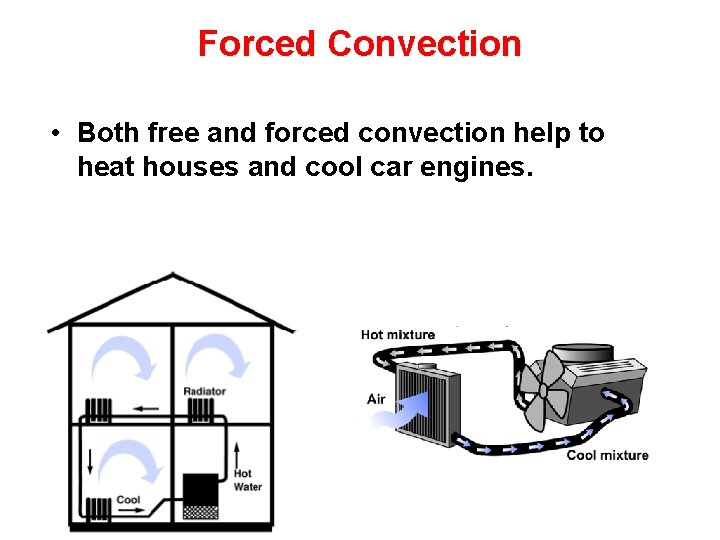
Forced Convection • Both free and forced convection help to heat houses and cool car engines.

Heat Convection Equation Heat transfer coefficient (watts/m 2 o. C) Heat flow (watts) Area contacting fluids (m 2) PH = h A (T 2 -T 1) Temperature difference (o. C)

Radiation Dr. AA Department of Chemical Engineering University Teknology Malaysia

Radiant Heat • We do not see thermal radiation because it occurs at infrared wavelengths invisible to the human eye. • Objects glow different colors at different temperatures.

26. 3 Radiant Heat • A rock at room temperature does not “glow”. • The curve for 20°C does not extend into visible wavelengths. • As objects heat up they start to give off visible light, or glow. • At 600°C objects glow dull red, like the burner on an electric stove.

Radiant Heat • As the temperature rises, thermal radiation produces shorterwavelength, higher energy light. • At 1, 000°C the color is yelloworange, turning to white at 1, 500°C. • If you carefully watch a bulb on a dimmer switch, you see its color change as the filament gets hotter. • The bright white light from a bulb is thermal radiation from an extremely hot filament, near 2, 600°C.

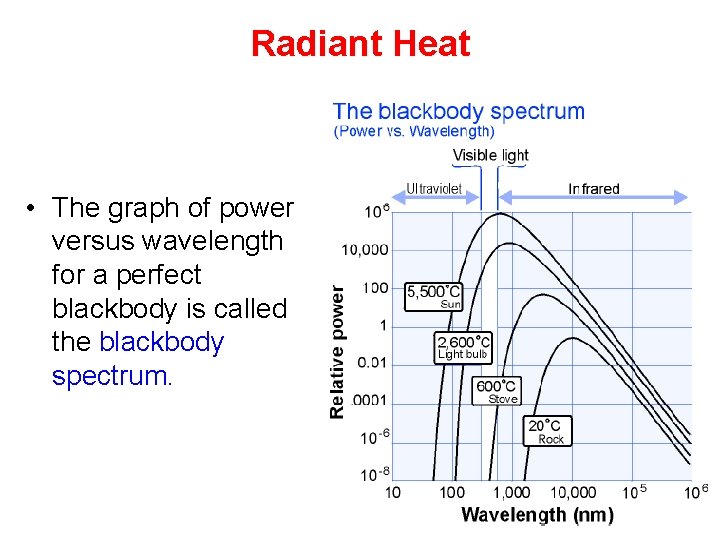
Radiant Heat • The graph of power versus wavelength for a perfect blackbody is called the blackbody spectrum.

Radiation striking a solid surface has one of three fates: 1. 2. 3. Absorption absorptivity (a) Transmission transmissivity (t) Reflection reflectivity (z) How are these properties related ? a + t +z=1

Two special cases require definition: If all of the energy is either reflected or absorbed (no transmitted radiation), we define the body as Opaque a + z = 1 If all of the energy striking a surface is absorbed, we define the body as Black body a = 1 For heat transfer calculations, we often assume that the properties a, t, and r are independent of wavelength. When this assumption is made we say that we have gray surfaces.

Let us return to the subject of radiation emitted by a surface. Total emissive power is defined as the total amount of energy leaving the surface per unit time per unit area: W = energy/area-time [Btu/hr-ft 2 or W/m 2] Note: Emissive power is a function of wavelength. The important wavelengths for heat transfer are 0. 5 -50 µm. For temperatures above 1500°F, the important wavelength range is between 0. 5 and 5 µm. In our analysis, we will use the average values over all wavelengths.

Emissivity The emissivity is the ratio of the emissive power of a surface compared to the maximum emissive power. How does the emissivity relate to the absorptivity (a) at thermal equilibrium? e=a Although this strictly applies at thermal equilibrium, we normally assume that it applies at all temperatures.

Stefan-Boltzman Law Finally, we must ask how the emissive power of a black body is related to temperature. The answer is provided by the Stefan Boltzman Law. W = s. T 4 where s = 0. 1714 x 10 -8 Btu/hr-ft 2 -°R 4 constant) = 5. 676 x 10 -8 W/m 2 -K 4 (Stefan-Boltzman For an object that is not a black body (i. e. , not a perfect radiator), we can write the following expression: W = es. T 4 T is absolute temperature

Heat Transfer Equation To calculate the heat transfer rate by radiation, we must include terms for energy output and energy received from the surroundings. Energy output: Energy input: Making the usual assumption that e = a, and multiplying by area yields: This is the expression for an object totally enclosed by surroundings at T∞.

View factors

View Factor Previously, we found that for a body totally enclosed by its surroundings, the net rate of heat transfer by thermal radiation is given by the following expression: q = es. A(Ts 4 - T 24) The equation for q given above is one of the most important and commonly used results, however, it does not cover all situations.

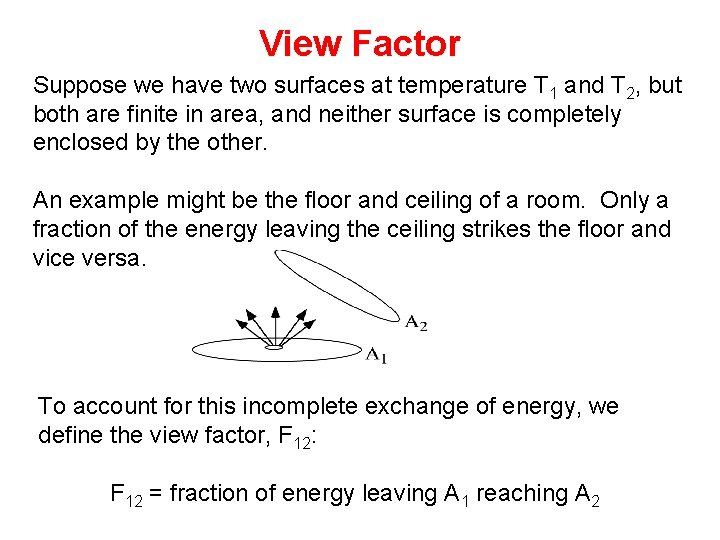
View Factor Suppose we have two surfaces at temperature T 1 and T 2, but both are finite in area, and neither surface is completely enclosed by the other. An example might be the floor and ceiling of a room. Only a fraction of the energy leaving the ceiling strikes the floor and vice versa. To account for this incomplete exchange of energy, we define the view factor, F 12: F 12 = fraction of energy leaving A 1 reaching A 2

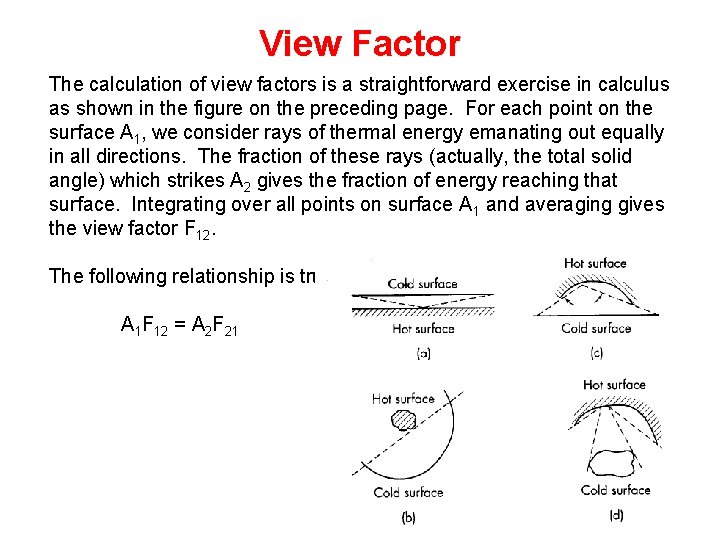
View Factor The calculation of view factors is a straightforward exercise in calculus as shown in the figure on the preceding page. For each point on the surface A 1, we consider rays of thermal energy emanating out equally in all directions. The fraction of these rays (actually, the total solid angle) which strikes A 2 gives the fraction of energy reaching that surface. Integrating over all points on surface A 1 and averaging gives the view factor F 12. The following relationship is true: A 1 F 12 = A 2 F 21

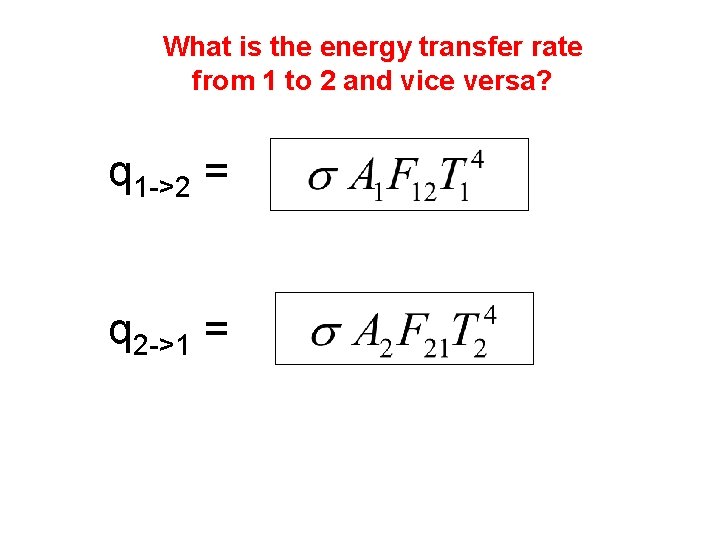
What is the energy transfer rate from 1 to 2 and vice versa? q 1 ->2 = q 2 ->1 =

Analytical Expression of View Factor Case 1: Differential surface parallel to a finite rectangular surface L 1 D L 2 where X=L 1/D and Y=L 2/D

Analytical Expression of View Factor b a c Case 2: Plane circular surface with common central normal where B = b/a and C = c/a

Analytical Expression of View Factor Case 3: Plane element A 1 to sphere of radius r 2; normal to centre of element passes through centre of sphere