Heat Transfer In Channels Flow Sarthit Toolthaisong 6

Heat Transfer In Channels Flow Sarthit Toolthaisong

6. 5 Channels with Uniform Surface Temperature We wish to determine the following: Sarthit Toolthaisong

6. 5 Channels with Uniform Surface Temperature Applying conservation of energy to the element dx Eq. (a) = Eq. (b), we get Sarthit Toolthaisong

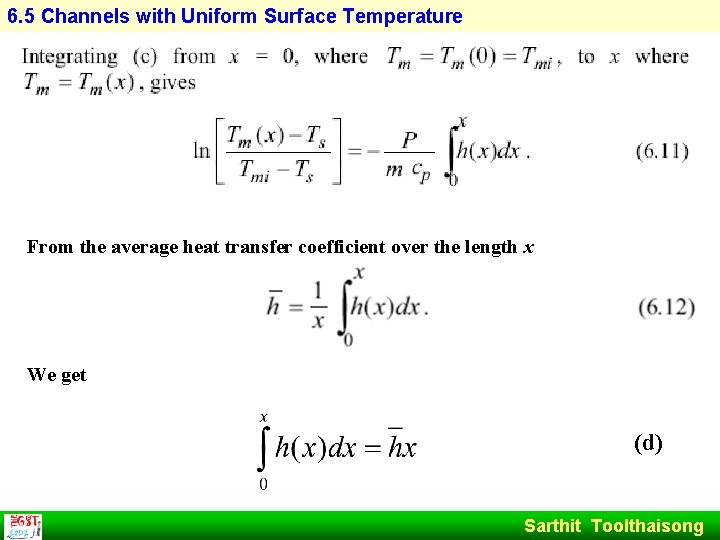
6. 5 Channels with Uniform Surface Temperature From the average heat transfer coefficient over the length x We get (d) Sarthit Toolthaisong

6. 5 Channels with Uniform Surface Temperature Introducing (d) into (6. 11) and solving the resulting equation for Tm(x) Application of conservation of energy between the inlet of the channel and a section x gives Application of Newton’s law of cooling gives the heat flux q”s(x) at location x gives Sarthit Toolthaisong

6. 5 Channels with Uniform Surface Temperature Sarthit Toolthaisong

6. 5 Channels with Uniform Surface Temperature Solution For flow through a tube at uniform surface temperature, applying Eq. (6. 13) At the outlet of the heat section (x=L) and solving for L Where Sarthit Toolthaisong

6. 5 Channels with Uniform Surface Temperature The properties of air using at the mean temperature Tm(x) Check the flow is laminar or turbulent Sarthit Toolthaisong

6. 5 Channels with Uniform Surface Temperature Since the Reynolds number is smaller than 2300, the flow is laminar. Thus The mass flow rate. Sarthit Toolthaisong

6. 5 Channels with Uniform Surface Temperature The perimeter. Finally, the length of tube Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D 6. 6. 1 Scale Analysis Equating Fourier’s law with Newton’s law A scale for r is Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D From Eq. (6. 18) applying thermal thickness of external flow Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D 6. 6. 2 Basic Considerations for the Analytical Determination of Heat Flux, Heat Transfer Coefficient and Nusselt Number (1) Fourier’s law and Newton’s law. (6. 21) Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D Substituting into (a) (6. 22) We define h using Newton’s law of cooling (6. 23) Combining (6. 22) and (6. 23) Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D Where Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D (2) The Energy Equation The last term in Eq. (6. 28) can be neglected for where Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D Thus, under such conditions, Eq. (6. 28) becomes 3) Mean (Bulk) Temperature, Tm Where Sarthit Toolthaisong

6. 6 Determination of Heat Transfer Coefficient h(x) and Nusselt Number Nu. D Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region This section focuses on the fully developed region. 6. 7. 1 Definition of Fully Developed Temperature Profile Far away from the entrance of a channel We introduce a dimensionless temperature For fully developed defined as is independent of x. That is Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region Thus. Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region 6. 7. 2 Heat Transfer Coefficient and Nusselt Number Equating Fourier’s with Newton’s law Using Eq. (6. 37) in the definition of the Nusselt number, give Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region For scale analysis of temperature gradient Compared Eq. (6. 19) Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region 6. 7. 3 Fully Developed Region for Tubes at Uniform Surface flux Application of Newton’s law of cooling gives Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region Using energy balance on element dx for detemine eq. (6. 41) Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region Assume Cp and m constant Substituting eq. (6. 42) into (6. 41) Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region For determine fluid temperature distribution T(r, x) and surface temperature Ts(x), from energy equation Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region The axial velocity for fully developed flow is Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region Substituting eq. (6. 46) and (6. 49) into (6. 32 a) gives Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region Substituting T(r, x), Tm(x) and Ts(x) into eq. (6. 33) gives Differentiating (6. 54) and substituting into (6. 38) gives the Nusselt number From scaling analysis Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region From eq. (6. 44) and (6. 50), we get Substituting (6. 51) into (6. 49) Surface temperature, by setting r=ro in (6. 52) Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region 6. 7. 4 Fully Developed Region for Tubes at Uniform Surface Temperature By energy equation - Neglecting axial conduction and dissipation - vr = 0 Simplifies to Boundary conditions Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region Using equation (6. 36 a) to eliminate Sarthit Toolthaisong

6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region Applied boundary condition to Eq. (6. 58) Sarthit Toolthaisong

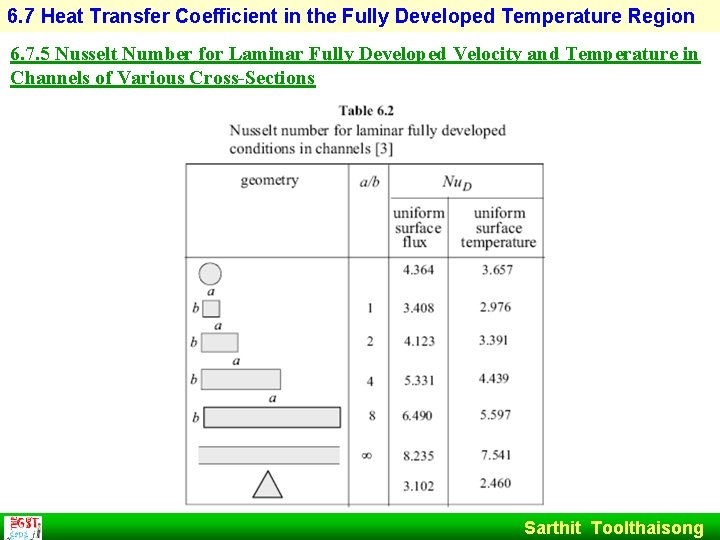
6. 7 Heat Transfer Coefficient in the Fully Developed Temperature Region 6. 7. 5 Nusselt Number for Laminar Fully Developed Velocity and Temperature in Channels of Various Cross-Sections Sarthit Toolthaisong

Example 6. 4: Maximum Surface Temperature in an Air Duct Solution Temperature distribution for uniform heat flux, given by eq. (6. 10) Sarthit Toolthaisong

Example 6. 4: Maximum Surface Temperature in an Air Duct Sarthit Toolthaisong

Example 6. 4: Maximum Surface Temperature in an Air Duct Using Energy conservation to determine L Sarthit Toolthaisong

Example 6. 4: Maximum Surface Temperature in an Air Duct Sarthit Toolthaisong

Example 6. 4: Maximum Surface Temperature in an Air Duct Laminar flow From Table. 6. 2 for uniform heat flux Sarthit Toolthaisong

Example 6. 4: Maximum Surface Temperature in an Air Duct Sarthit Toolthaisong

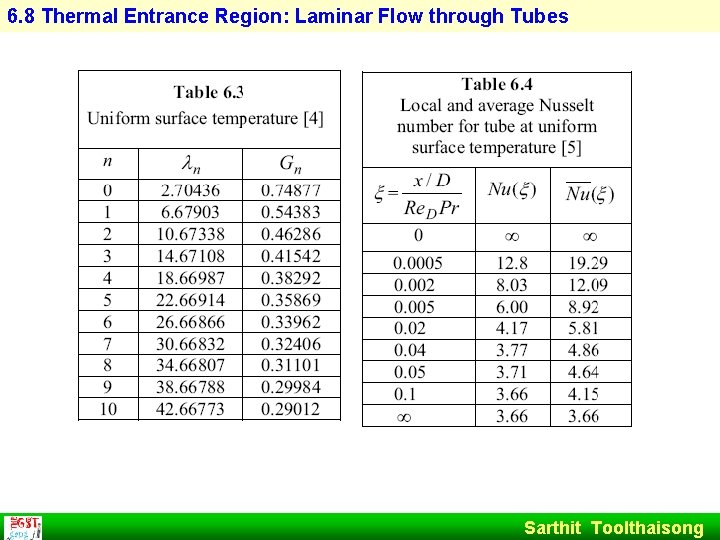
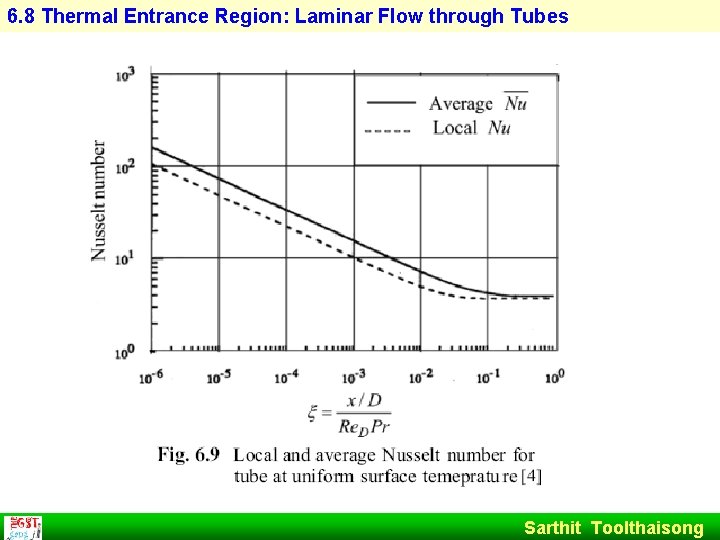
6. 8 Thermal Entrance Region: Laminar Flow through Tubes 6. 8. 1 Uniform Surface Temperature: Graetz Solution Consider laminar flow in Fig. 6. 8 Fluid enters a heated or cooled section with a fully developed velocity We neglect axial conduction (Pe >100) Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes Assume product solution as the form Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes Substitution the solution of (b) and (c) into (a) Where Cn is constant Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes The surface heat flux is given by Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes Sarthit Toolthaisong

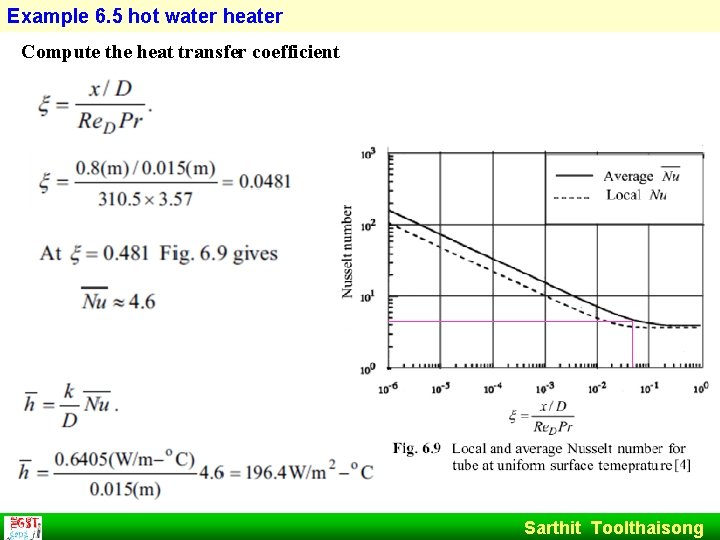
Example 6. 5 hot water heater Solution For flow through the tube at uniform surface temperature, from Eq. (6. 13) Sarthit Toolthaisong

Example 6. 5 hot water heater Sarthit Toolthaisong

Example 6. 5 hot water heater Sarthit Toolthaisong

Example 6. 5 hot water heater Compute thermal entrance length, from Eq. (6. 6) Sarthit Toolthaisong

Example 6. 5 hot water heater Compute the heat transfer coefficient Sarthit Toolthaisong

Example 6. 5 hot water heater Sarthit Toolthaisong

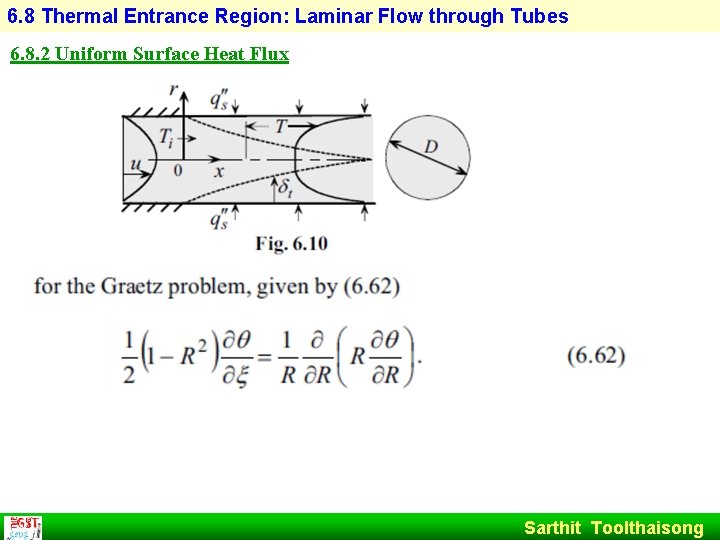
6. 8 Thermal Entrance Region: Laminar Flow through Tubes 6. 8. 2 Uniform Surface Heat Flux Sarthit Toolthaisong

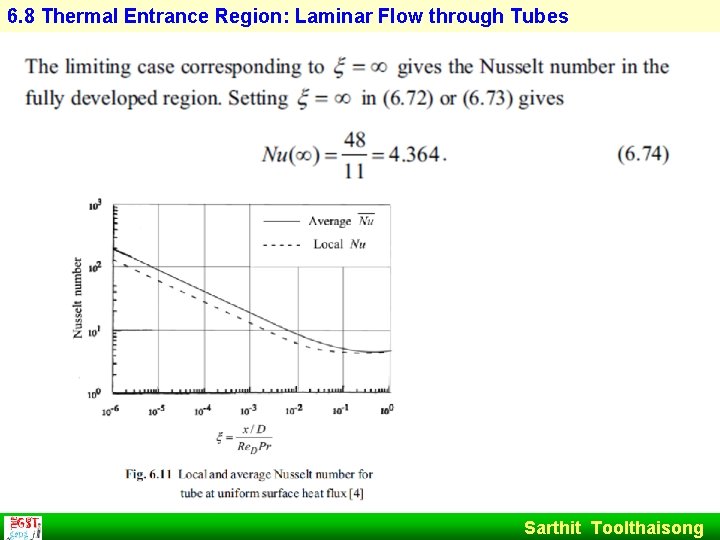
6. 8 Thermal Entrance Region: Laminar Flow through Tubes The solution for Nusselt number is Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes The average Nusselt number is given by. Sarthit Toolthaisong

6. 8 Thermal Entrance Region: Laminar Flow through Tubes Sarthit Toolthaisong