Heat Equation and its applications in imaging processing

Heat Equation and its applications in imaging processing and mathematical biology Yongzhi Xu Department of Mathematics University of Louisville, KY 40292

1. Introduction

System of ‘heat equations’

2. Derivation of heat equation 2. 1. Random walks

2. 2. Fick’s law

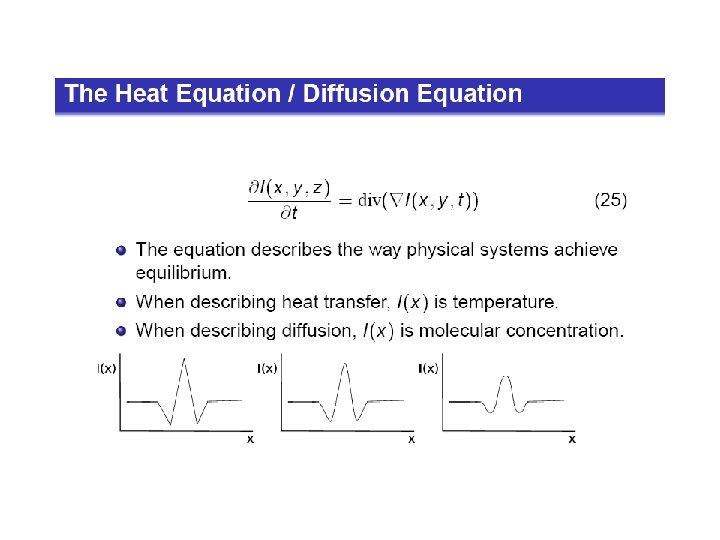
Then the balance law implies

3. Applications of heat equation 1. Heat equation in image processing 2. Heat equation in cancer model and spatial ecological model

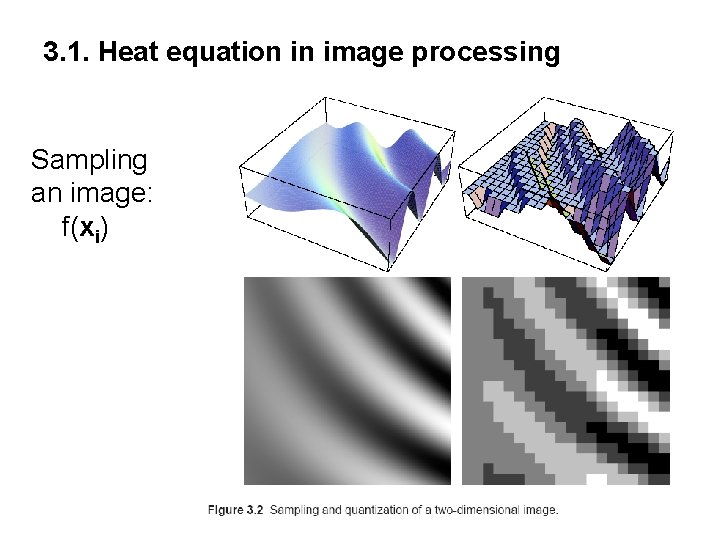
3. 1. Heat equation in image processing Sampling an image: f(xi)

Three components of image processing: 1. Image Compression

2. Image Denoising

3. Image Analysis

One common need: Smoothing • Smoothing is a necessary part of image formation. • An image can be correctly represented by a discrete set of values, the samples, only if it has been previously smoothed.

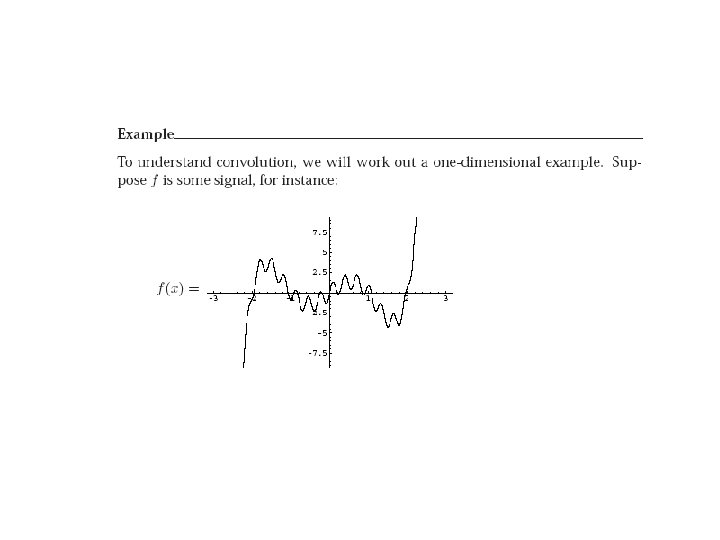
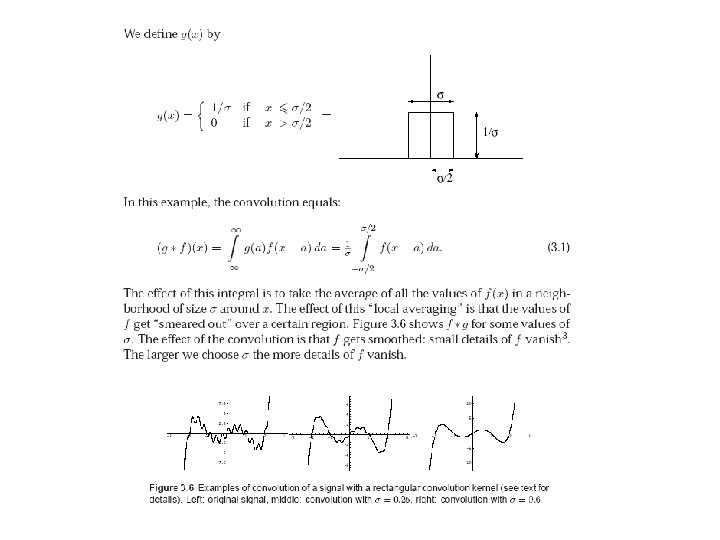
How to smooth a image? ------ Convolution with a ‘bell-shaped’ function

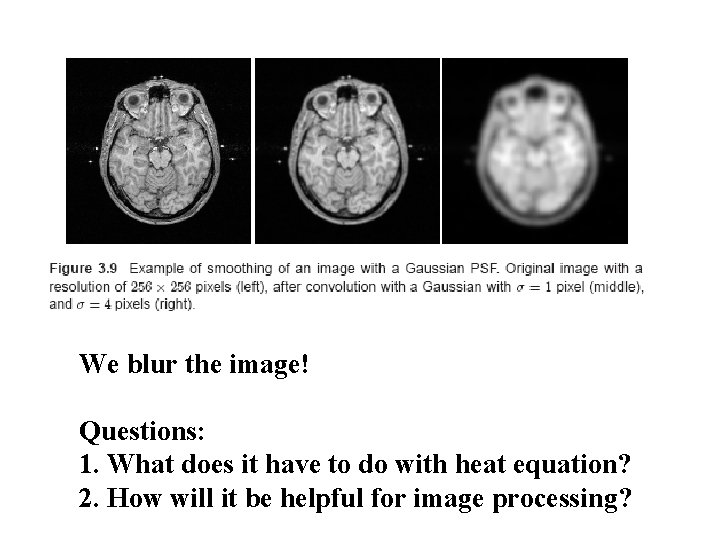
We blur the image! Questions: 1. What does it have to do with heat equation? 2. How will it be helpful for image processing?

Answer to question 1:

Modified heat equations and applications: • Deblur an image by reversing time in the heat equation:

• Smoothing to detect edges

Level curves

3. 2: Reaction-diffusion Models and Pattern Formations • Let U(x, t) and V(x, t) be the density functions of two chemicals or species which interact or react Alan Turing, “The Chemical Basis of Morphogenesis, ” Phil. Trans. Roy. Soc. (1952). Acknowledgement: Pictures of animal patterns are from Junping Shi’s website.

Mathematical Biology by James Murray Emeritus Professor University of Washington, Seattle Oxford University, Oxford http: //www. amath. washington. edu/people/faculty/murray/

Why do animals’ coats have different patterns?

Murray’s theory Murray suggests that a single mechanism could be responsible for generating all of the common patterns observed. This mechanism is based on a reaction-diffusion system of the morphogen prepatterns, and the subsequent differentiation of the cells to produce melanin simply reflects the spatial patterns of morphogen concentration.

Reaction-diffusion systems • Domain: rectangle (0, a) X (0, b) • Boundary conditions: head and tail (no flux), body side (periodic)

“Theorem 1”: Snakes always have striped (ring) patterns, but not spotted patterns. Turing-Murray Theory: snake is the example of b/a is large.

Snake pictures (stripe patterns)

“Theorem 2”: There is no animal with striped body and spotted tail, but there is animal with spotted body and striped tail. Turing-Murray theory: The same reaction-diffusion mechanism should be responsible for the patterns on both body and tail. The body is always wider than the tail. If the body is striped, then the tail must also be striped.

More examples: Spotted body and striped tail Genet (left), Giraffe (right)

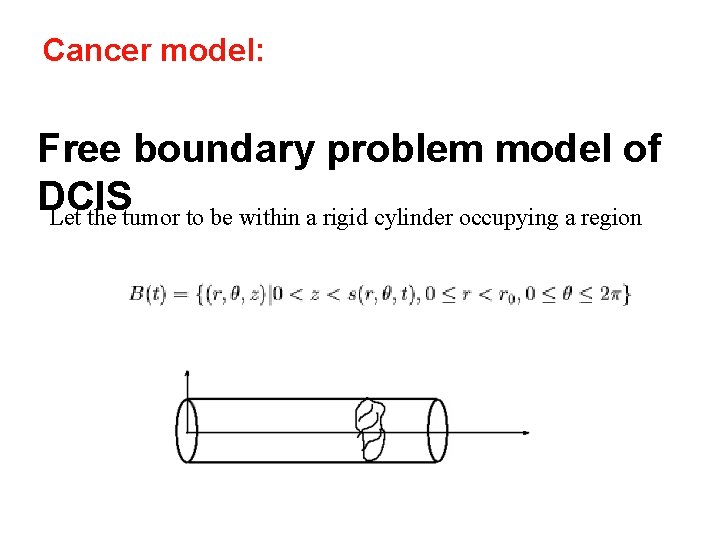
Cancer model: Free boundary problem model of DCIS Let the tumor to be within a rigid cylinder occupying a region

--- the growing boundary of the tumor --- the dimensionless nutrient concentration in the surrounding --- the rate of surrounding transfer per unit length --- the transfer of nutrient from surrounding --- the nutrient consumption rate --- the ratio of the nutrient diffusion time scale To the tumor growth time scale. C<<1. --- the nutrient concentration

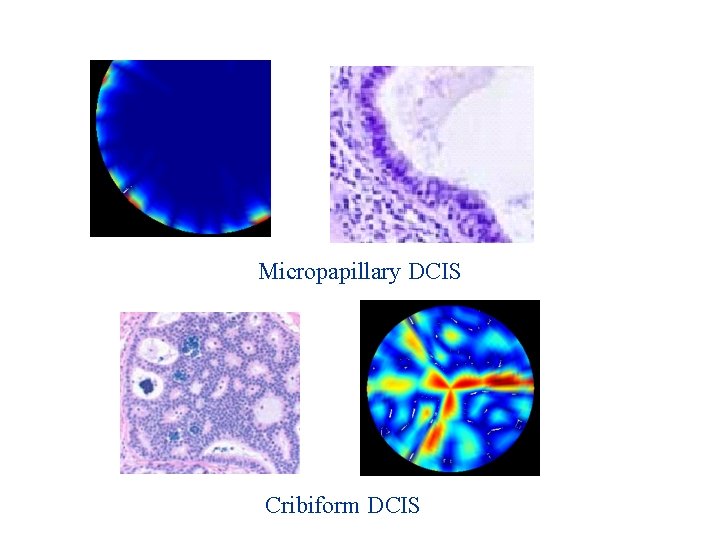
Micropapillary DCIS Cribiform DCIS

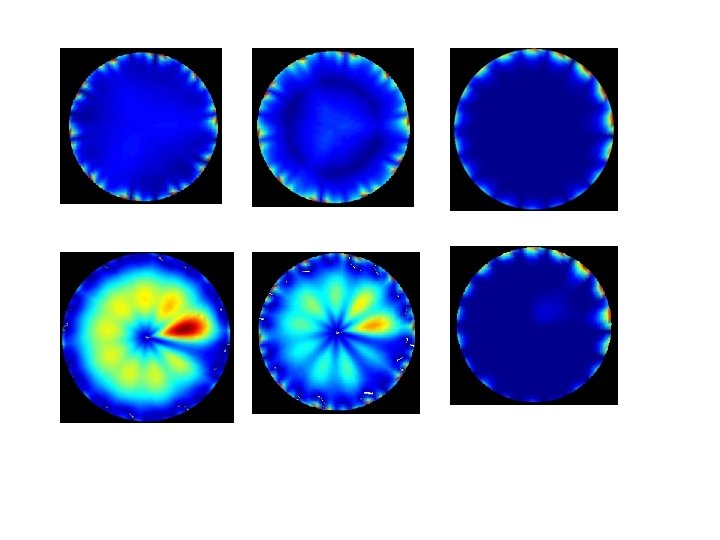
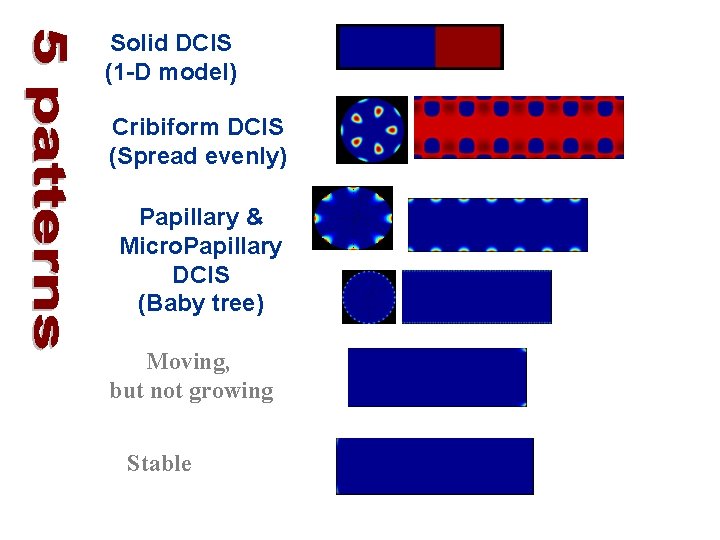
Solid DCIS (1 -D model) Cribiform DCIS (Spread evenly) Papillary & Micro. Papillary DCIS (Baby tree) Moving, but not growing Stable

More sophisticate models may be considered. (I) mixed models

(II) segregated models

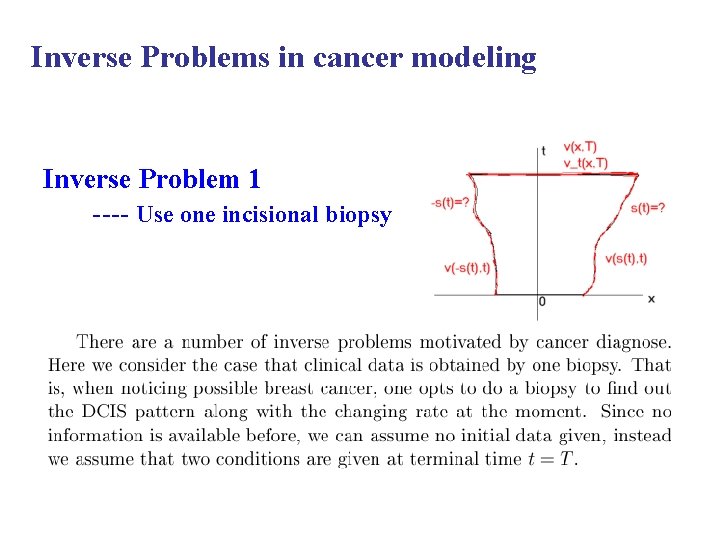
Inverse Problems in cancer modeling Inverse Problem 1 ---- Use one incisional biopsy

Inverse Problem 2 --- use a sequence of needle biopsy

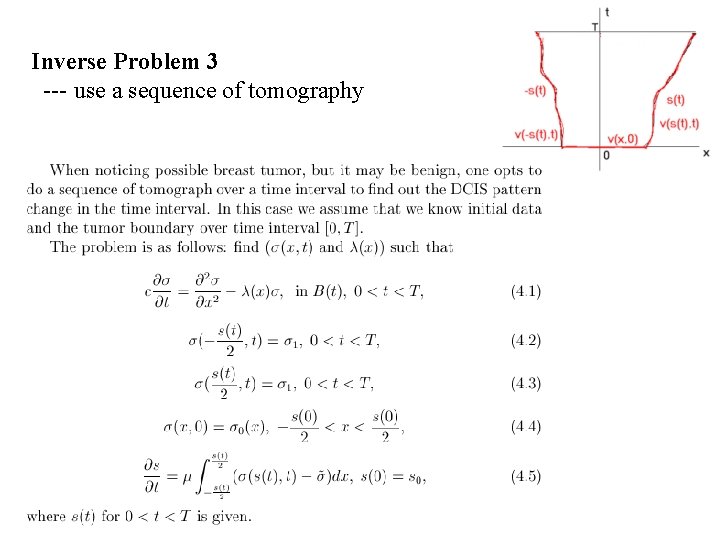
Inverse Problem 3 --- use a sequence of tomography

Acknowledgement: Some of the graphs and pictures are copied from the manuscript of Frederic Guichard and Jean-Michel Morel, and from the website of Junping Shi.

Thank You!