Heat and Mass Transfer in Spray FreezeDrying Alina

Heat and Mass Transfer in Spray Freeze-Drying Alina A. Alexeenko School of Aeronautics & Astronautics, Purdue University In collaboration with Israel Sebastiao, Purdue University Dr Tom Robinson, Aerosol Theurapeutics CPPR 2016: Freeze Drying of Pharmaceuticals & Biologicals Conference

Heat Transfer in Freeze-Drying Freeze-drying qgas Advantages: • Established, validated aseptic processes and equipment • Simple process models Challenges: • Heat transfer is highly inefficient: qcontact • Fluid and shelves have high thermal inertia • Low pressures: • Viscous losses Contact: qcontact=f(Tshelf, Tprod, vial) • Sensing is difficult/expensive Radiation: qrad=f(Tshelf, Tprod, Twall) • Open loop controls • Container presents heat and mass Gas: qgas=qcond + qconv transfer barrier Gas convection: qconv=f(pch, Tprod, Twall) qrad 2

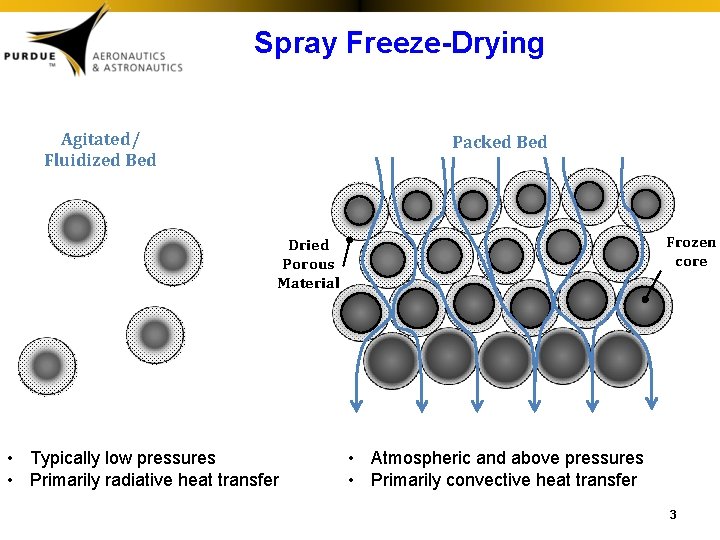
Spray Freeze-Drying Bed Packed Agitated/ Fluidized Bed Frozen core Dried Porous Material • Typically low pressures • Primarily radiative heat transfer • Atmospheric and above pressures • Primarily convective heat transfer 3

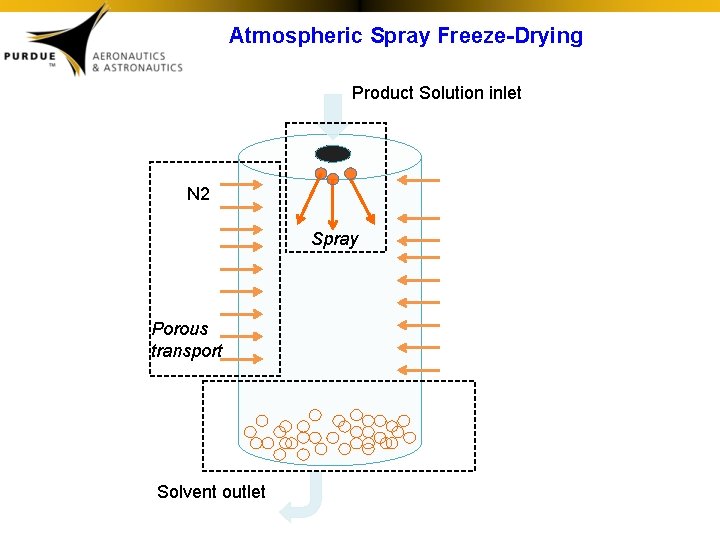
Atmospheric Spray Freeze-Drying Product Solution inlet N 2 Spray Porous transport Solvent outlet

Atmospheric Spray Freeze-Drying Three main processes that comprise a typical ASFD cycle: 1)Spray atomization 2)Heat transfer within the chamber and 3)Drying

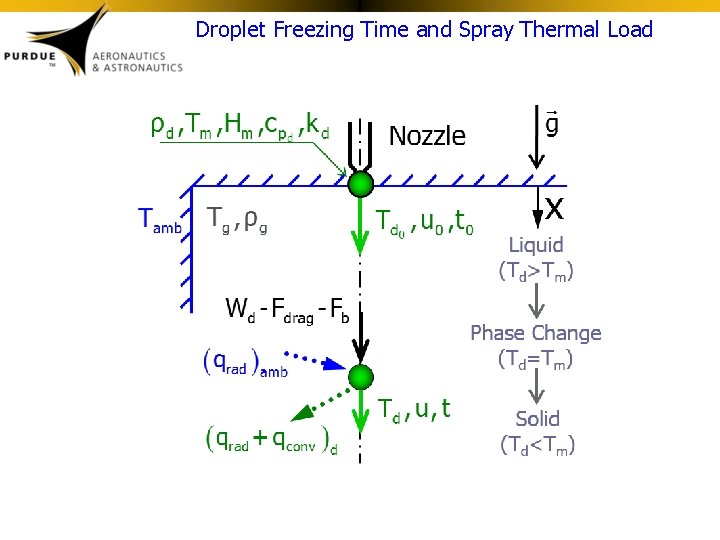
Droplet Freezing Time and Spray Thermal Load

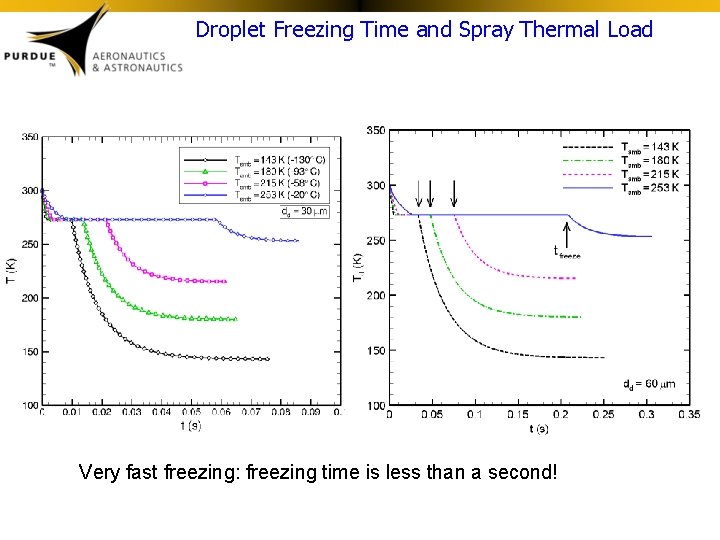
Droplet Freezing Time and Spray Thermal Load Very fast freezing: freezing time is less than a second!

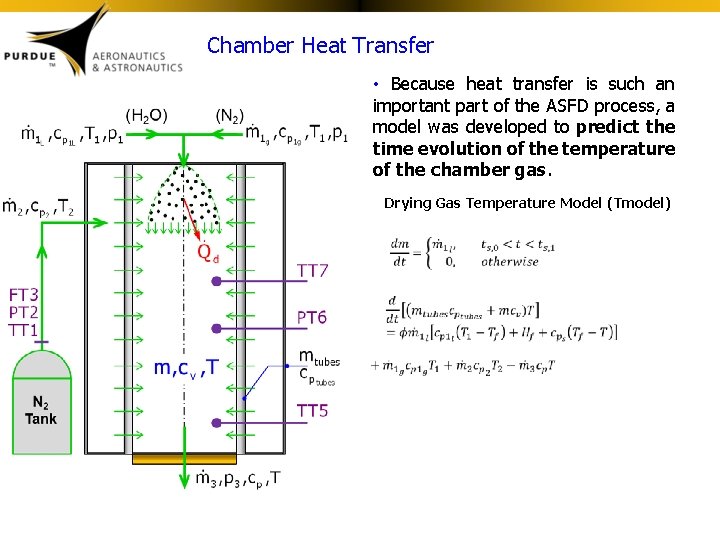
Chamber Heat Transfer • Because heat transfer is such an important part of the ASFD process, a model was developed to predict the time evolution of the temperature of the chamber gas. Drying Gas Temperature Model (Tmodel)

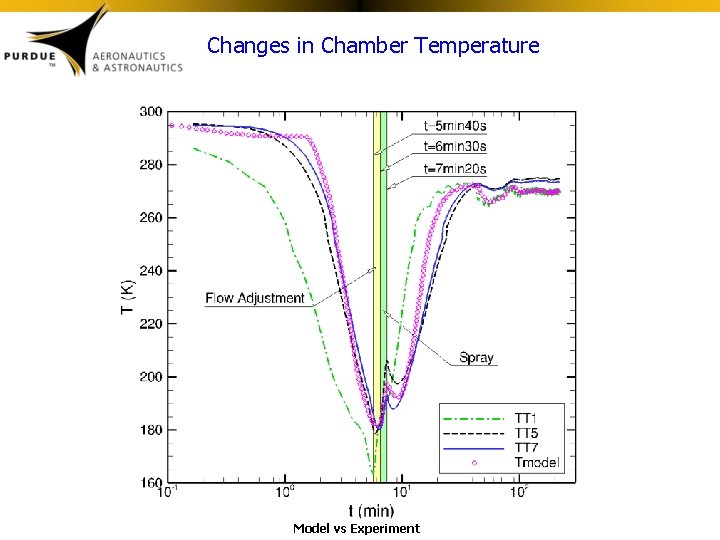
Changes in Chamber Temperature Model vs Experiment

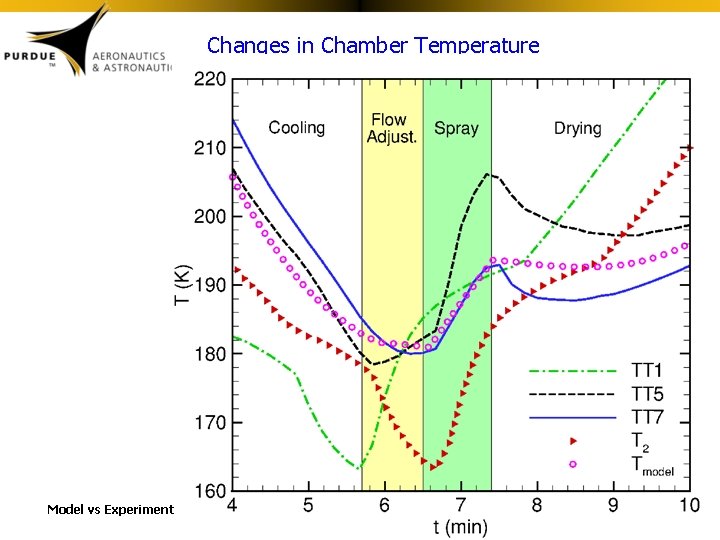
Changes in Chamber Temperature Model vs Experiment

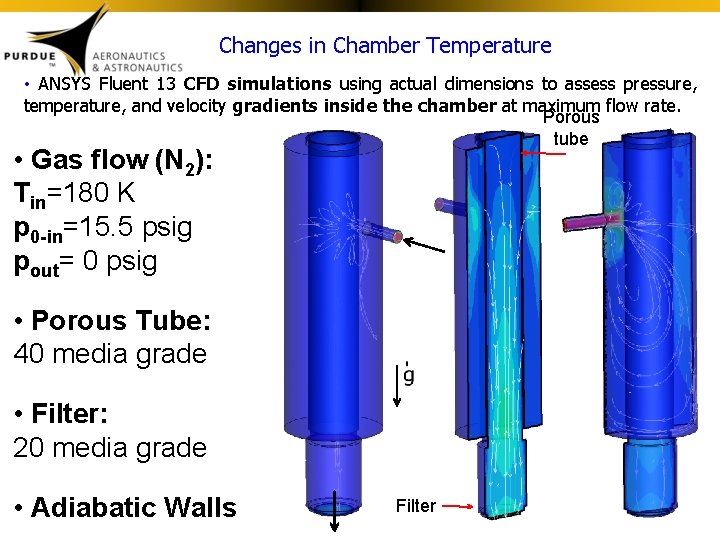
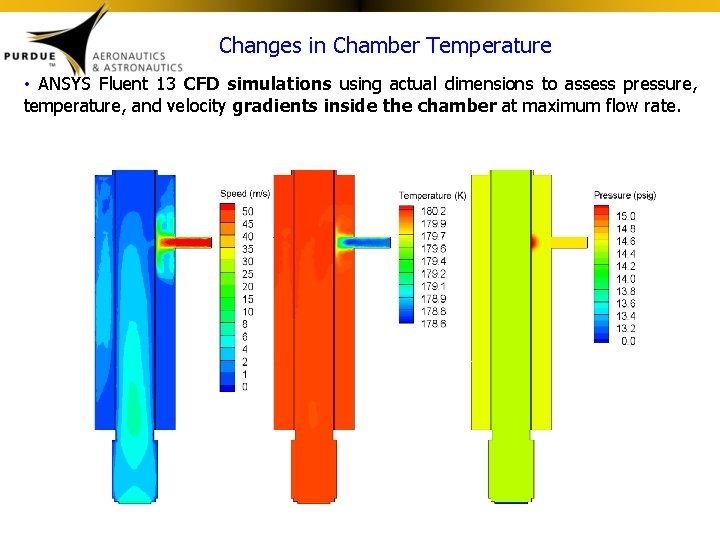
Changes in Chamber Temperature • ANSYS Fluent 13 CFD simulations using actual dimensions to assess pressure, temperature, and velocity gradients inside the chamber at maximum flow rate. Porous tube • Gas flow (N 2): Tin=180 K p 0 -in=15. 5 psig pout= 0 psig • Porous Tube: 40 media grade • Filter: 20 media grade • Adiabatic Walls Filter

Changes in Chamber Temperature • ANSYS Fluent 13 CFD simulations using actual dimensions to assess pressure, temperature, and velocity gradients inside the chamber at maximum flow rate.

Estimation of Drying Time • Mass and energy conservation equations are employed to describe the evolution of the powder moisture content. These equations are combined with data from ASFD runs to obtain a temperature-dependent correlation to estimate the drying time. • In the following slides, Datasets 1 -2 are runs with 10% BSA solutions whereas Dataset 3 is a run with 20% BSA.

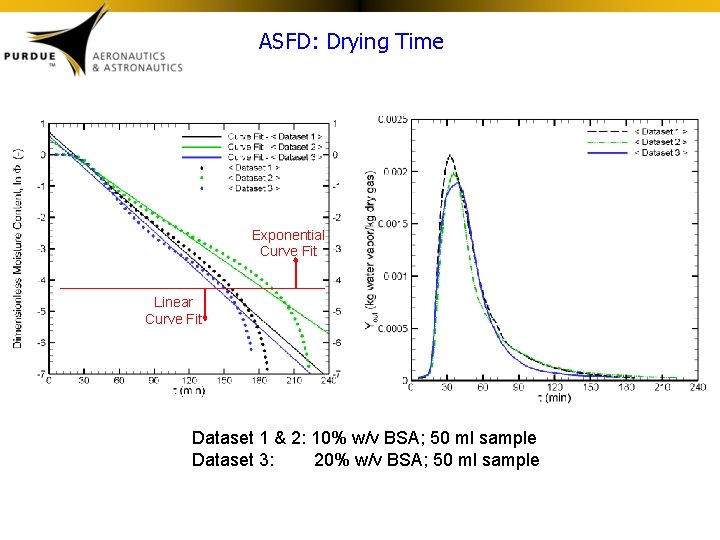
ASFD: Drying Time Exponential Curve Fit Linear Curve Fit Dataset 1 & 2: 10% w/v BSA; 50 ml sample Dataset 3: 20% w/v BSA; 50 ml sample

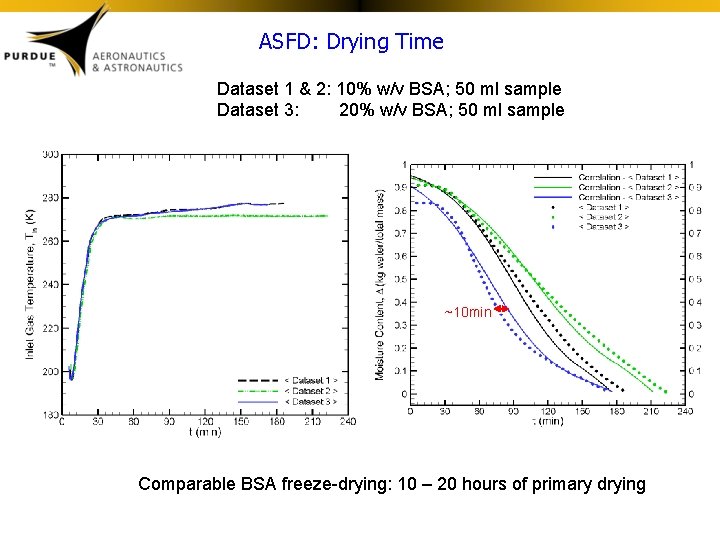
ASFD: Drying Time Dataset 1 & 2: 10% w/v BSA; 50 ml sample Dataset 3: 20% w/v BSA; 50 ml sample ~10 min Comparable BSA freeze-drying: 10 – 20 hours of primary drying

Low-Pressure Spray Freeze-Drying • Even faster drying rates for suspended particles due to radiant heating • Complex heat and mass transfer: • Very rarefied flow around particles – free molecular flow around particle! • Additional forces, e. g. thermophoretic may induce particle motion Thermophoresis movie

Summary • Extremely fast drying (< 1 sec!) is possible for typical spray freeze-drying and is expected to be beneficial for protein stability • Drying times could be lower by about an order of magnitude than for typical freeeze-drying • Fast response time due to lower viscosity working fluid – LN 2 vapor vs silicone oil liquids is beneficial for closed-loop control • Development of simple process models is a major need for adopting spray freeze-drying in bio/pharmaceutical manufacturing. THANK YOU!! CPPR 2012 17