Heart Rate Variability Measures and Models Outline o

Heart Rate Variability: Measures and Models 指導教授：鄭仁亮 學生：曹雅婷

Outline o o Introduction Methods n n o Conventional Point Process Fractal Point Process Measure n n Standard Measures Novel Measures

Introduction o ECG a recording of the cardiac-induced skin potentials at the body’s surface o HRV called heart rate variability, the variability of the RR-interval sequence

Methods o o o The heartbeat sequence as a point process. The sequence of heartbeats can be studied by replacing the complex waveform of an individual heartbeat recorded in the ECG. The sequence of heartbeats is represented by

ECG Analysis

Conventional Point Process o Simplest n o homogeneous Poisson point process Related point process n n nonparalyzable fixed-dead-time modified Poisson point process gamma-γ renewal process

Homogeneous Poisson point process o The interevent-interval probability density function where λ is the mean number of events per unit time. o interevent-interval mean=1/λ o interevent-interval variance=1/λ 2

Dead-time modified Poisson point process o The interevent-interval probability density function 0 Here τd is the dead time and λ is the rate of the process before dead time is imposed.

Fractal Point Process o o Fractal stochastic processes exhibit scaling in their statistics. Suppose changing the scale by any factor a effectively scales the statistic by some other factor g(a), related to the factor but independent of the original scale: w(ax) = g(a)w(x).

Fractal Point Process o o The only nontrivial solution of this scaling equation, for real functions and arguments, that is independent of a and x is w(x) = bg(x) with g(x) = xc The particular case of fixed a admits a more general solution g(x; a) = xc cos[2πln(x)/ ln(a)]

Standard Frequency-Domain Measures o A rate-based power spectral density n o An interval-based power spectral density n o Units of sec-1 Units of cycles/interval To convert the interval-based frequency to the time-based frequency using

Estimate the spectral density 1. 2. 3. Divided data into K nonoverlapping blocks of L samples Hanning window Discrete Fourier transform of each block

Measures in HRV o VLF. The power in the very-low-frequency range: 0. 003– 0. 04 cycles/interval. o LF. The power in the low-frequency range: 0. 04– 0. 15 cycles/interval. o HF. The power in the high-frequency range: 0. 15– 0. 4 cycles/interval. o LF/HF. The ratio of the low-frequency- range power to that in the high-frequency range.

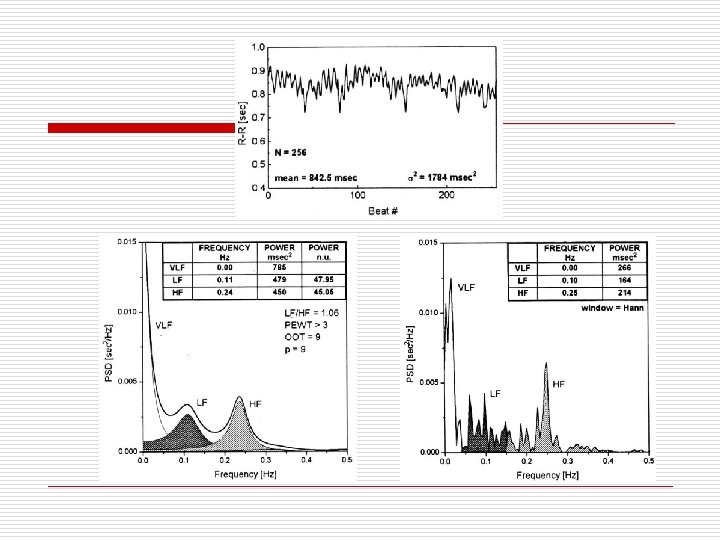
Standard Time-Domain Measures o p. NN 50. proportion of successive NN intervals o SDANN. Standard Deviation of the Average NN interval o SDNN. Standard Deviation of the NN interval

Other Standard Measures o o The event-number histogram The Fano factor

Novel Scale-Dependent Measures o Allen Factor [A(T)] n The Allan factor is the ratio of the eventnumber Allan variance to twice the mean:

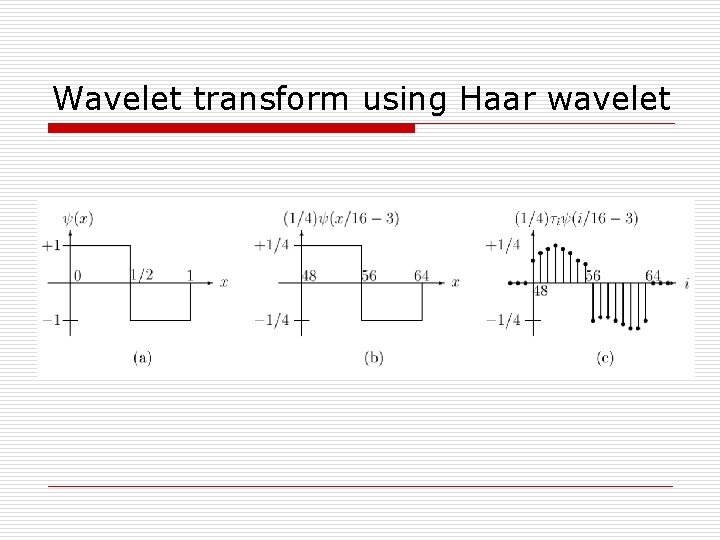
Wavelet transform using Haar wavelet