Hearing Biomechanics STANDING WAVES Principle of Superposition If

Hearing Biomechanics STANDING WAVES

Principle of Superposition If two or more waves combine at a given point, the resulting disturbance is the sum of the disturbances of the individual waves. Two traveling waves can pass through each other without being destroyed or even altered!

Some Results of Superposition Two waves, same wavelength and frequency, opposite direction: Standing Wave Two waves, same wavelength and frequency, similar direction, different phase: Interference Two waves, same direction, slightly different frequency and wavelength: Beats

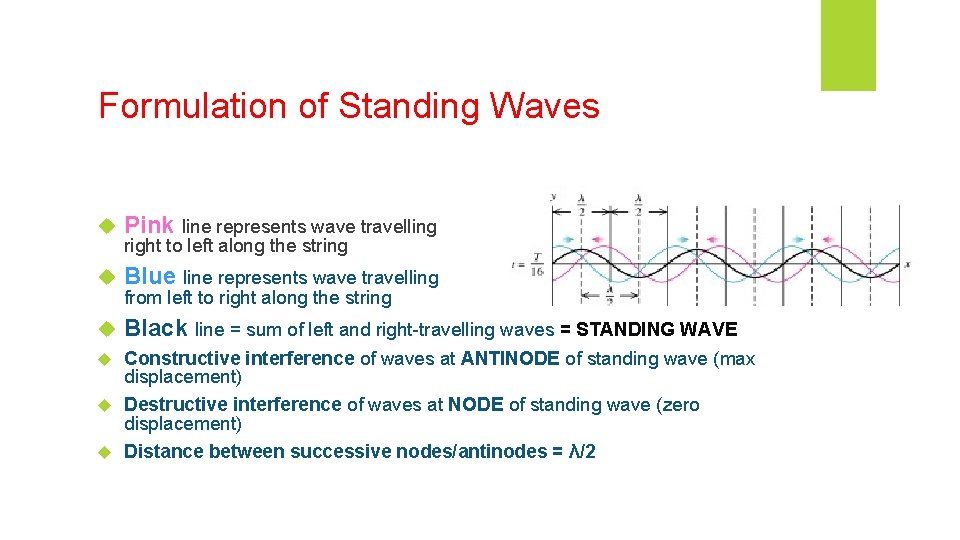
Formulation of Standing Waves Pink line represents wave travelling Blue line represents wave travelling Black line = sum of left and right-travelling waves = STANDING WAVE right to left along the string from left to right along the string Constructive interference of waves at ANTINODE of standing wave (max displacement) Destructive interference of waves at NODE of standing wave (zero displacement) Distance between successive nodes/antinodes = λ/2

Mathematical formulation of Standing Waves Wave moving right to left (pink wave) Wave moving left to right (blue wave) Total wave function (black wave): • Amplitude depends on position • Zero y-displacement (node) when sin(kx) = 0 • Maximum y-displacement (y=2 A) when sin(kx)=+/- 1

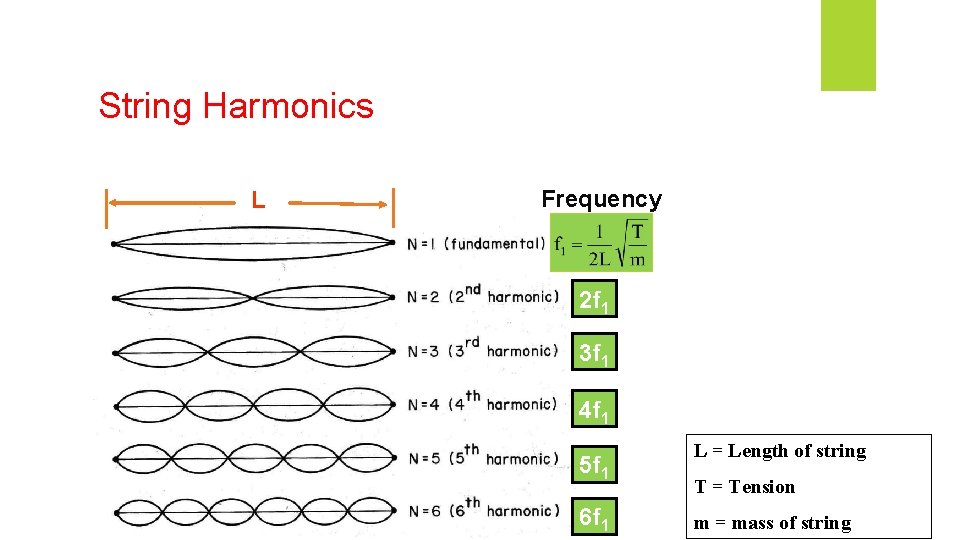
String Harmonics L Frequency 2 f 1 3 f 1 4 f 1 5 f 1 6 f 1 L = Length of string T = Tension m = mass of string

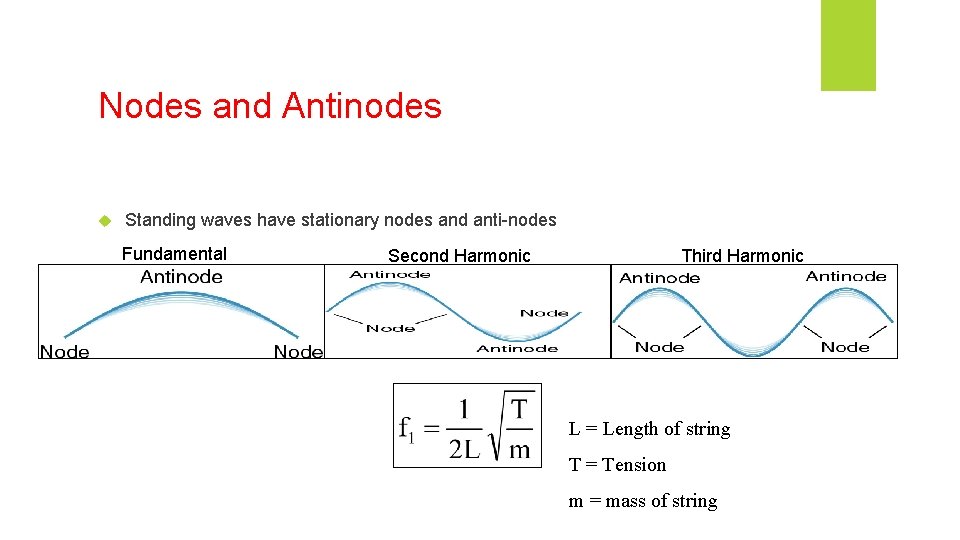
Nodes and Antinodes Standing waves have stationary nodes and anti-nodes Fundamental Second Harmonic Third Harmonic L = Length of string T = Tension m = mass of string

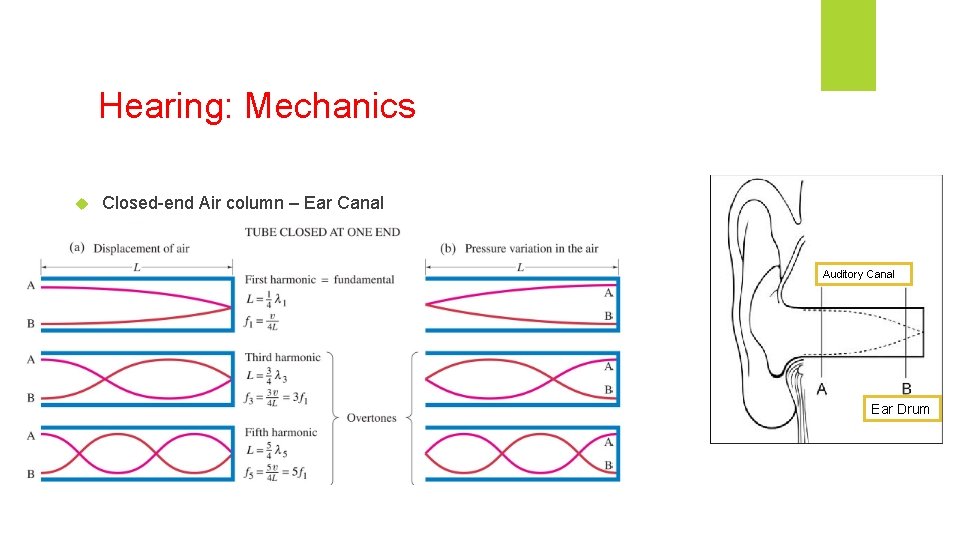
Hearing: Mechanics Closed-end Air column – Ear Canal Auditory Canal Ear Drum

Hearing: Mechanics Red particles: extremes of motion

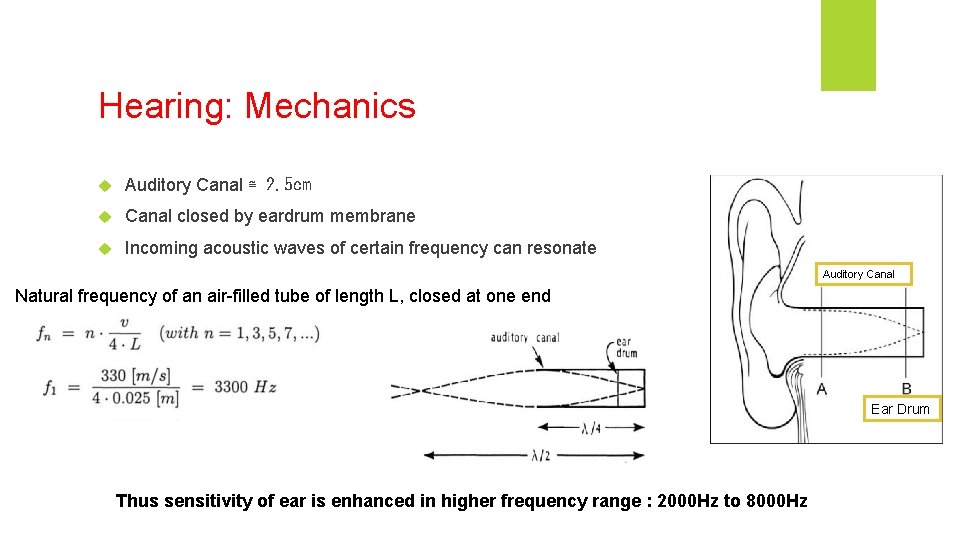
Hearing: Mechanics Auditory Canal ≅ 2. 5 cm Canal closed by eardrum membrane Incoming acoustic waves of certain frequency can resonate Auditory Canal Natural frequency of an air-filled tube of length L, closed at one end Ear Drum Thus sensitivity of ear is enhanced in higher frequency range : 2000 Hz to 8000 Hz

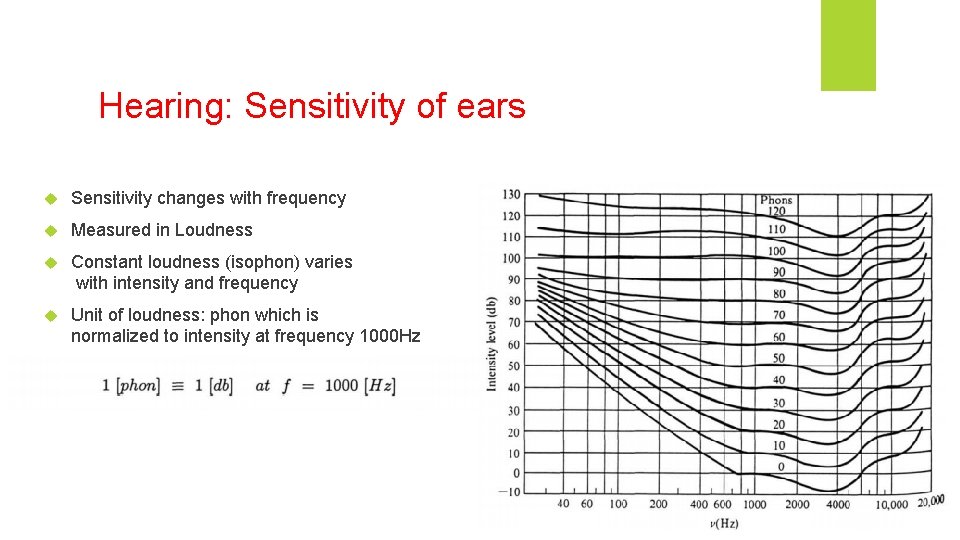
Hearing: Sensitivity of ears Sensitivity changes with frequency Measured in Loudness Constant loudness (isophon) varies with intensity and frequency Unit of loudness: phon which is normalized to intensity at frequency 1000 Hz

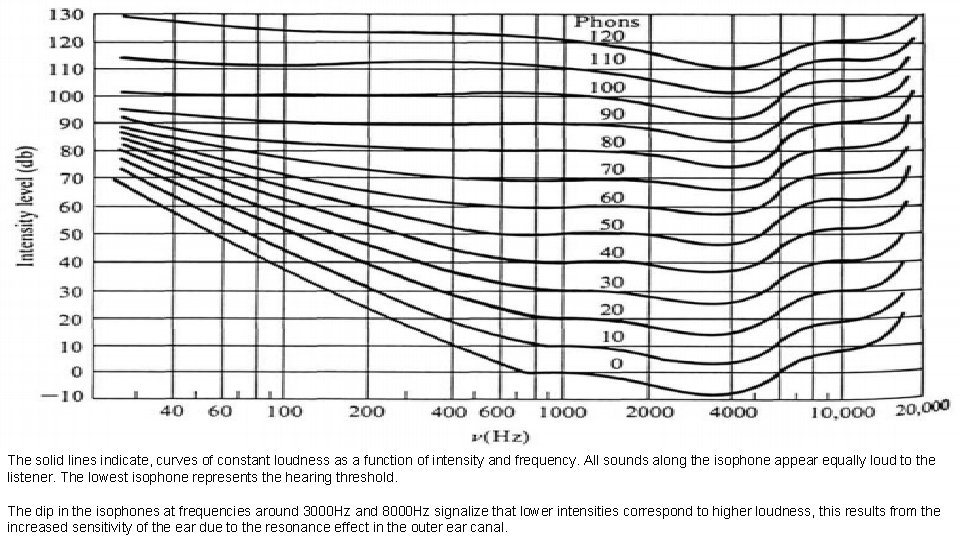
The solid lines indicate, curves of constant loudness as a function of intensity and frequency. All sounds along the isophone appear equally loud to the listener. The lowest isophone represents the hearing threshold. The dip in the isophones at frequencies around 3000 Hz and 8000 Hz signalize that lower intensities correspond to higher loudness, this results from the increased sensitivity of the ear due to the resonance effect in the outer ear canal.

Are standing waves only perceived Healthy ear – all frequencies within audible limit – 20 Hz to 20 k. Hz At frequencies of Standing waves Resonance At resonant frequencies, sound gets amplified

Boundary Behavior Reflection and Transmission Reflection Free boundary From low to high density Fixed boundary From high to low density

Reflection and Transmission at Eardrum Partial reflection and transmission Minimize Reflection and Maximize Transmission = Optimized Hearing Sensitivity

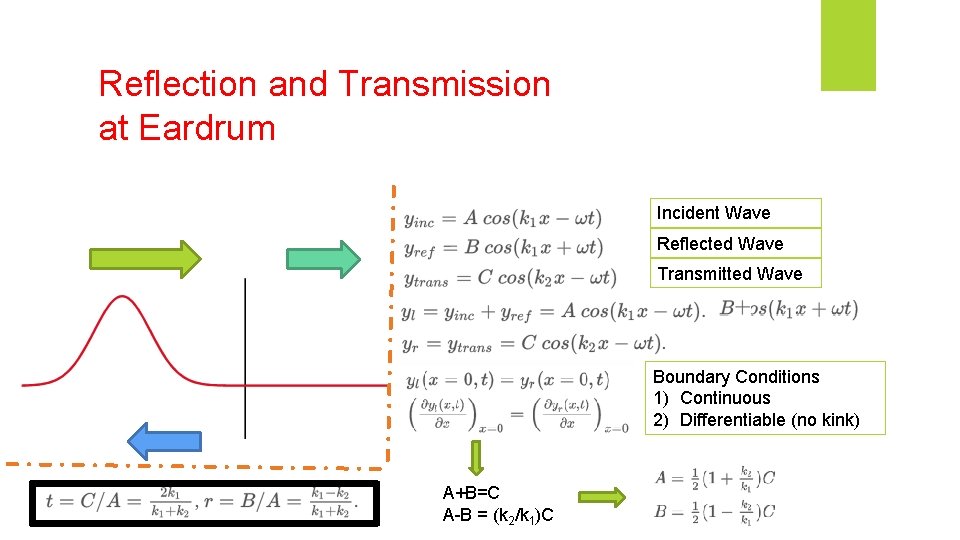
Reflection and Transmission at Eardrum Incident Wave Reflected Wave Transmitted Wave Boundary Conditions 1) Continuous 2) Differentiable (no kink) A+B=C A-B = (k 2/k 1)C

Reflection and Transmission at Eardrum Z = ��. �� Impedance = Density. Speed Sound 2 Intensity ∝ (Amplitude)