Heapsort Overview v Time complexity On logn v

Heapsort

Overview: v Time complexity – O(n log(n)) v Consider we have an array to be sorted. v The idea is to construct a binary tree depending on the array, with each node being larger than its children (Heapifing), that leads the root to be the largest in the array. v Then we remove the root from the list and reheap. v Repeat the whole process as long as we have more than one node in the tree.

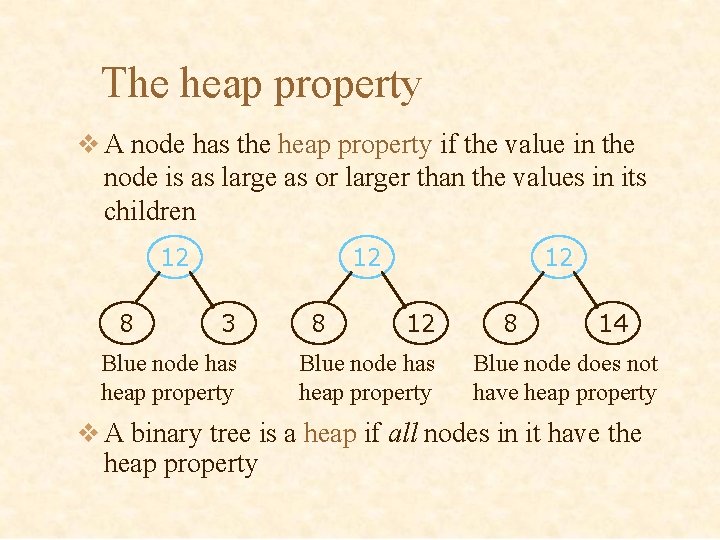
The heap property v A node has the heap property if the value in the node is as large as or larger than the values in its children 12 8 12 3 Blue node has heap property 8 12 12 Blue node has heap property 8 14 Blue node does not have heap property v A binary tree is a heap if all nodes in it have the heap property

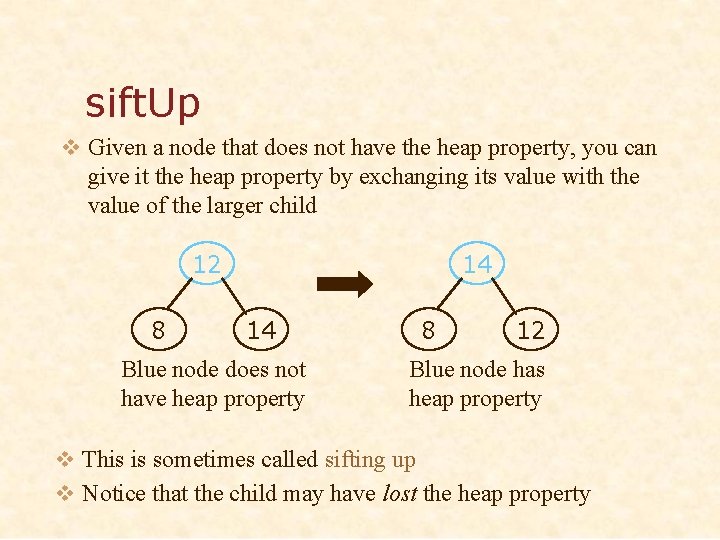
sift. Up v Given a node that does not have the heap property, you can give it the heap property by exchanging its value with the value of the larger child 12 8 14 14 Blue node does not have heap property 8 12 Blue node has heap property v This is sometimes called sifting up v Notice that the child may have lost the heap property

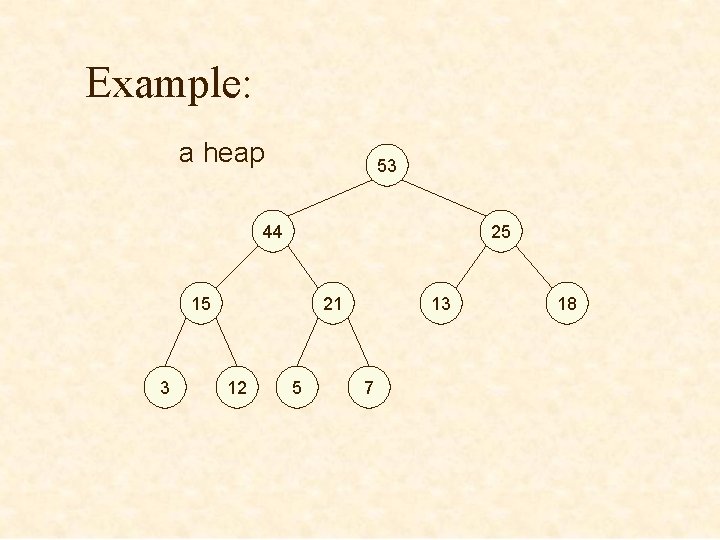
Example: a heap 53 44 25 15 3 21 12 5 13 7 18

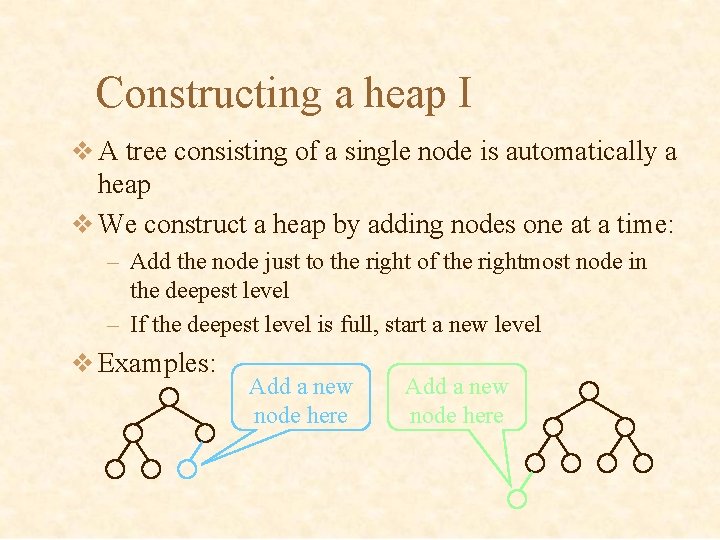
Constructing a heap I v A tree consisting of a single node is automatically a heap v We construct a heap by adding nodes one at a time: – Add the node just to the right of the rightmost node in the deepest level – If the deepest level is full, start a new level v Examples: Add a new node here

Constructing a heap II v Each time we add a node, we may destroy the heap property of its parent node v To fix this, we sift up v But each time we sift up, the value of the topmost node in the sift may increase, and this may destroy the heap property of its parent node v We repeat the sifting up process, moving up in the tree, until either – We reach nodes whose values don’t need to be swapped (because the parent is still larger than both children), or – We reach the root

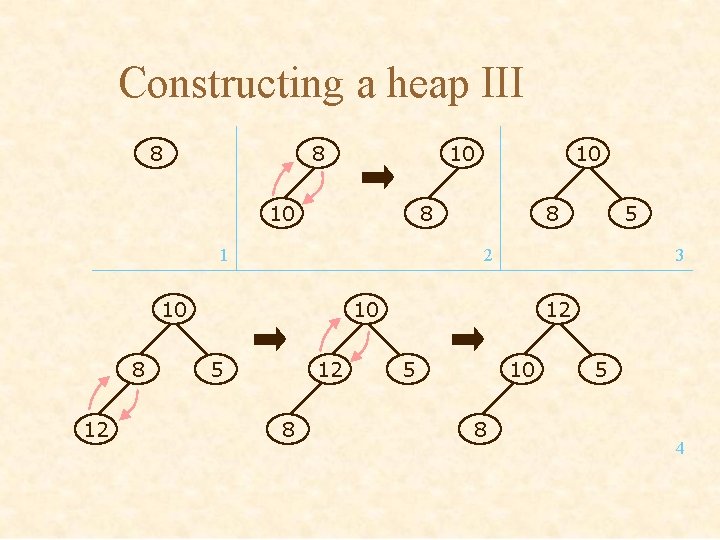
Constructing a heap III 8 8 10 10 8 1 12 8 5 2 10 8 10 3 10 5 12 8 12 5 10 8 5 4

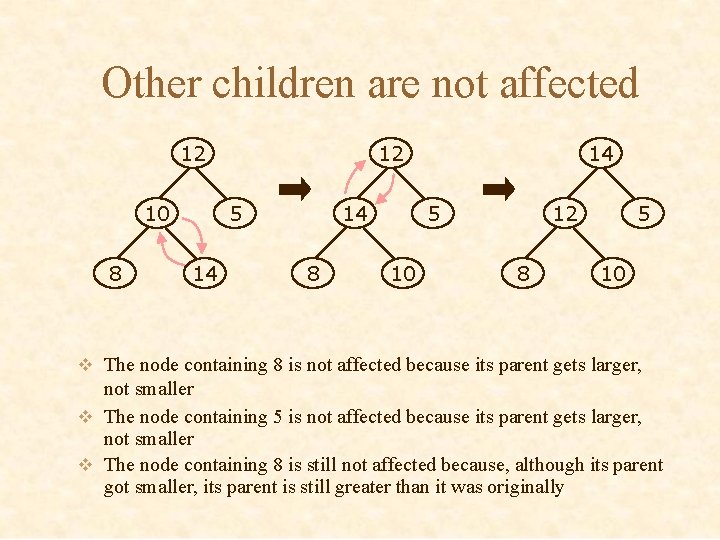
Other children are not affected 12 10 8 12 5 14 14 8 14 5 10 12 8 5 10 v The node containing 8 is not affected because its parent gets larger, not smaller v The node containing 5 is not affected because its parent gets larger, not smaller v The node containing 8 is still not affected because, although its parent got smaller, its parent is still greater than it was originally

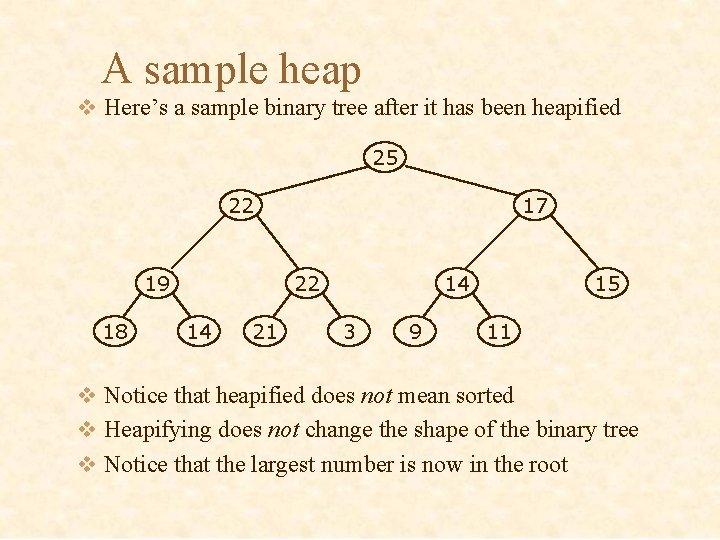
A sample heap v Here’s a sample binary tree after it has been heapified 25 22 19 18 17 22 14 21 14 3 9 15 11 v Notice that heapified does not mean sorted v Heapifying does not change the shape of the binary tree v Notice that the largest number is now in the root

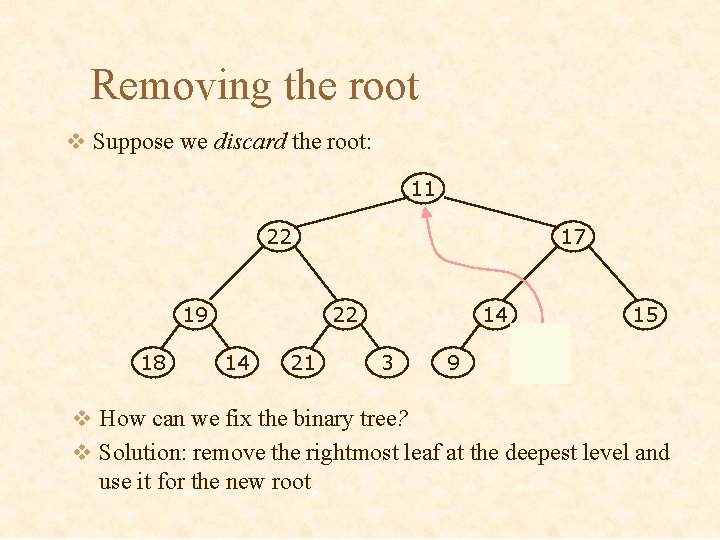
Removing the root v Suppose we discard the root: 11 22 19 18 17 22 14 21 14 3 9 15 11 v How can we fix the binary tree? v Solution: remove the rightmost leaf at the deepest level and use it for the new root

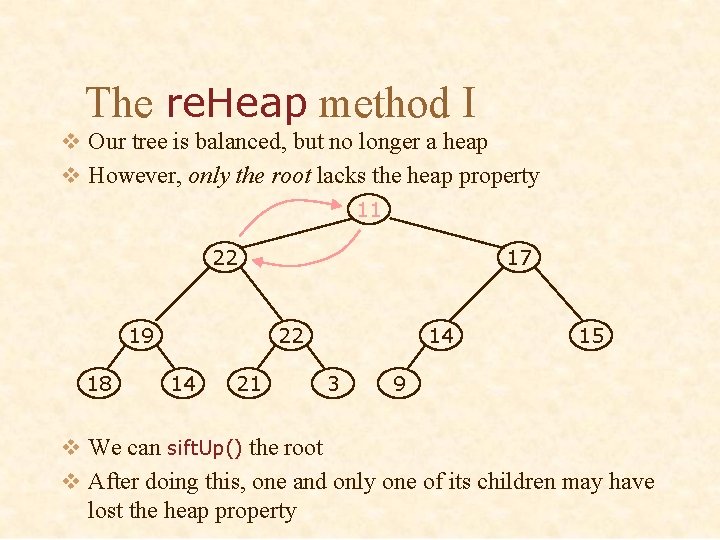
The re. Heap method I v Our tree is balanced, but no longer a heap v However, only the root lacks the heap property 11 22 19 18 17 22 14 21 14 3 15 9 v We can sift. Up() the root v After doing this, one and only one of its children may have lost the heap property

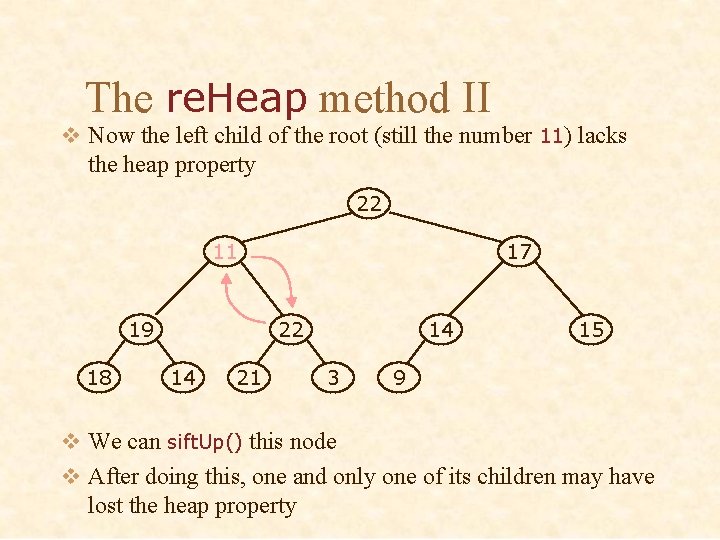
The re. Heap method II v Now the left child of the root (still the number 11) lacks the heap property 22 11 19 18 17 22 14 21 14 3 15 9 v We can sift. Up() this node v After doing this, one and only one of its children may have lost the heap property

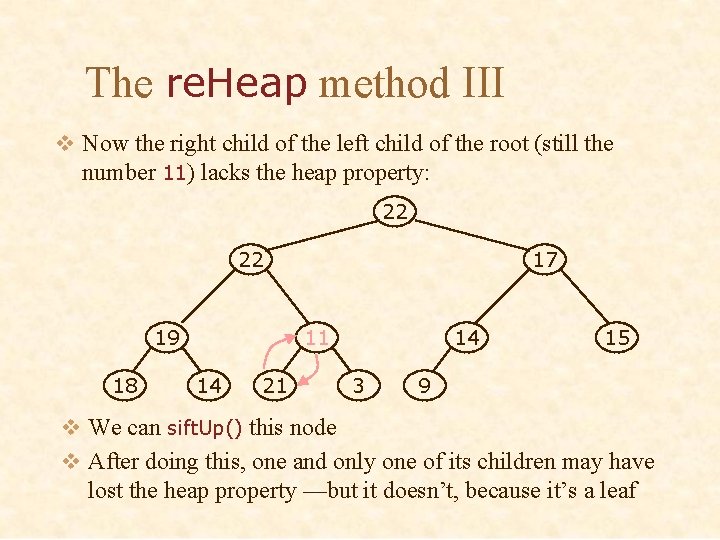
The re. Heap method III v Now the right child of the left child of the root (still the number 11) lacks the heap property: 22 22 19 18 17 11 14 21 14 3 15 9 v We can sift. Up() this node v After doing this, one and only one of its children may have lost the heap property —but it doesn’t, because it’s a leaf

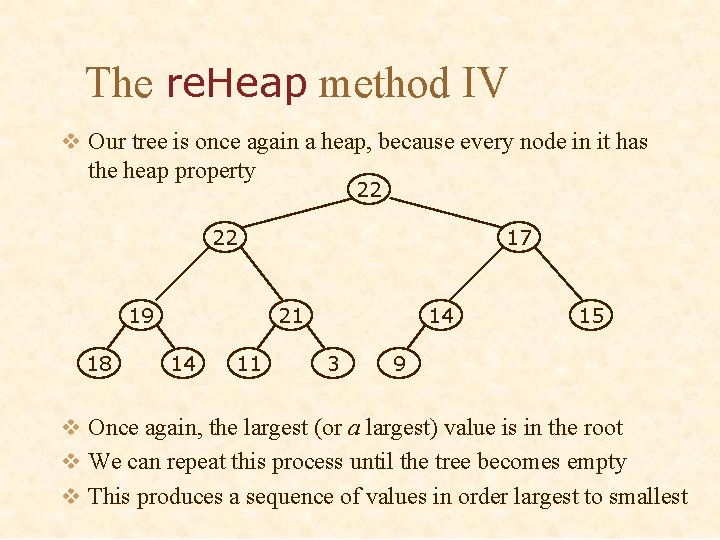
The re. Heap method IV v Our tree is once again a heap, because every node in it has the heap property 22 22 19 18 17 21 14 11 14 3 15 9 v Once again, the largest (or a largest) value is in the root v We can repeat this process until the tree becomes empty v This produces a sequence of values in order largest to smallest

Sorting v What do heaps have to do with sorting an array? v Here’s the neat part: – Because the binary tree is balanced, it can be represented as an array – All our operations on binary trees can be represented as operations on arrays – To sort: heapify the array; while the array isn’t empty { remove and replace the root; reheap the new root node; }

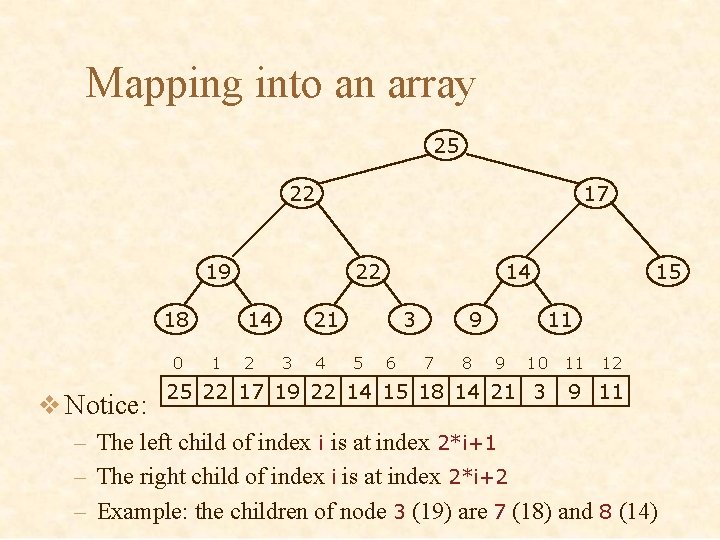
Mapping into an array 25 22 17 19 18 0 22 14 1 2 14 21 3 4 3 5 6 9 7 8 15 11 9 10 25 22 17 19 22 14 15 18 14 21 3 11 12 9 11 v Notice: – The left child of index i is at index 2*i+1 – The right child of index i is at index 2*i+2 – Example: the children of node 3 (19) are 7 (18) and 8 (14)

Removing and replacing the root v The “root” is the first element in the array v The “rightmost node at the deepest level” is the last element v Swap them. . . 0 1 2 3 4 5 6 7 8 9 10 25 22 17 19 22 14 15 18 14 21 3 0 1 2 3 4 5 6 7 8 9 10 11 22 17 19 22 14 15 18 14 21 3 11 12 9 11 11 12 9 25 v. . . And pretend that the last element in the array no longer exists—that is, the “last index” is 11 (9)

Reheap and repeat v Reheap the root node (index 0, containing 11). . . 0 1 2 3 4 5 6 7 8 9 10 11 22 17 19 22 14 15 18 14 21 3 0 1 2 3 4 5 6 7 8 9 10 22 22 17 19 21 14 15 18 14 11 3 0 1 2 3 4 5 6 7 8 9 10 11 12 9 25 11 12 9 22 17 19 22 14 15 18 14 21 3 22 25 v. . . And again, remove and replace the root node v Remember, though, that the “last” array index is changed v Repeat until the last becomes first, and the array is sorted!

Algorithm Step 1. Build Heap – O(n) - Build binary tree taking N items as input, ensuring the heap structure property is held, in other words, build a complete binary tree. - Heapify the binary tree making sure the binary tree satisfies the Heap Order property. Step 2. Perform n delete. Max operations – O(log(n)) - Delete the maximum element in the heap – which is the root node, and place this element at the end of the sorted array.

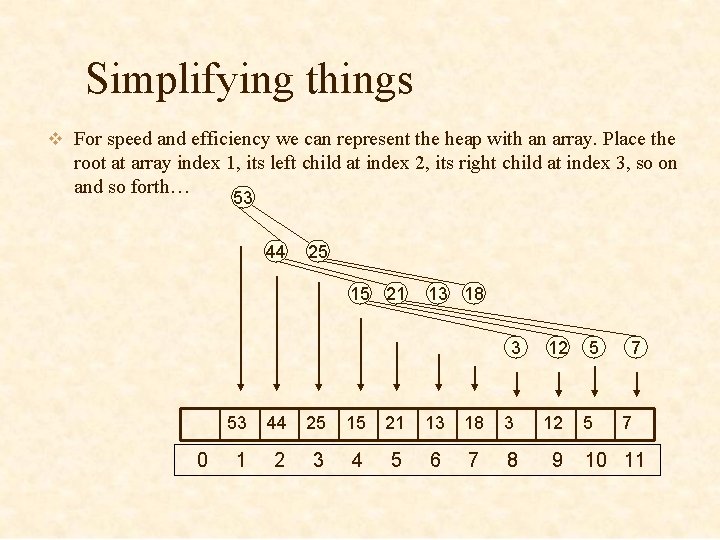
Simplifying things v For speed and efficiency we can represent the heap with an array. Place the root at array index 1, its left child at index 2, its right child at index 3, so on and so forth… 53 44 25 15 21 13 18 3 0 12 53 44 25 15 21 13 18 3 12 1 2 3 4 5 6 7 8 9 5 5 7 7 10 11

53 44 25 15 21 13 18 3 0 12 53 44 25 15 21 13 18 3 12 1 2 3 4 5 6 7 8 9 5 5 7 7 10 11

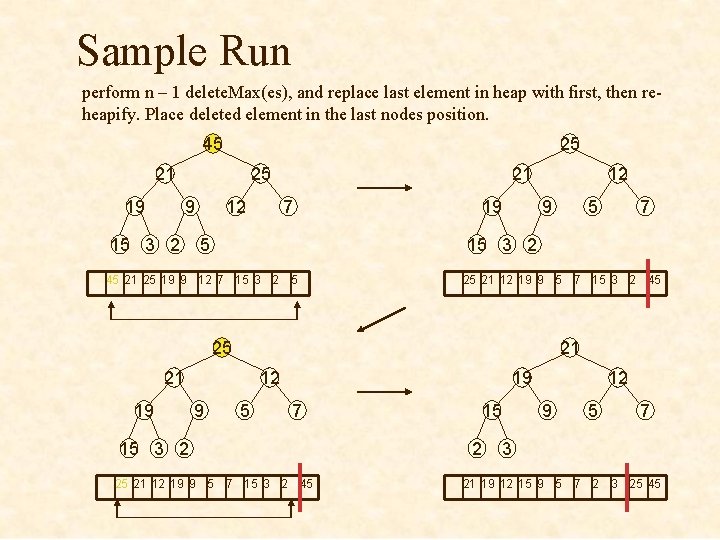
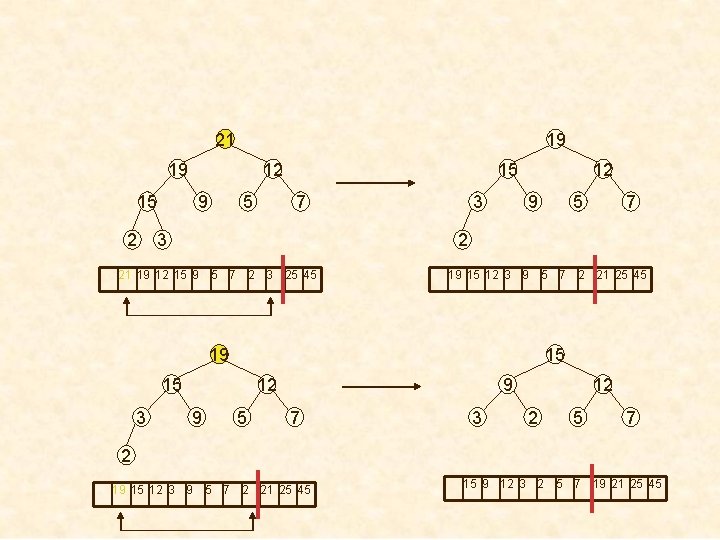
Sample Run perform n – 1 delete. Max(es), and replace last element in heap with first, then reheapify. Place deleted element in the last nodes position. 45 25 21 19 25 9 15 3 2 12 21 7 19 12 9 25 21 12 19 9 5 7 15 3 2 45 25 21 21 12 9 7 15 3 2 5 45 21 25 19 9 12 7 15 3 2 5 19 5 5 19 7 15 3 2 25 21 12 19 9 5 7 15 3 2 45 15 2 12 9 5 7 3 21 19 12 15 9 5 7 2 3 25 45

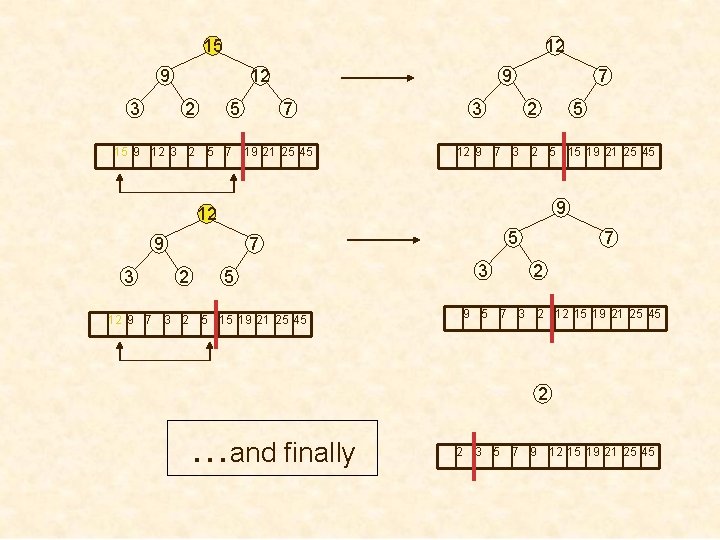
21 19 19 15 2 12 9 5 15 7 3 3 12 9 7 2 21 19 12 15 9 5 7 2 3 25 45 19 15 12 3 9 5 7 2 21 25 45 19 15 15 3 5 12 9 5 9 7 3 12 2 5 7 2 19 15 12 3 9 5 7 2 21 25 45 15 9 12 3 2 5 7 19 21 25 45

15 12 9 3 12 2 5 9 7 15 9 12 3 2 5 7 19 21 25 45 3 7 2 5 12 9 7 3 2 5 15 19 21 25 45 9 12 9 3 5 7 2 5 12 9 7 3 2 5 15 19 21 25 45 3 7 2 9 5 7 3 2 12 15 19 21 25 45 2 …and finally 2 3 5 7 9 12 15 19 21 25 45

Conclusion v 1 st Step- Build heap, O(n) time complexity v 2 nd Step – perform n delete. Max operations, each with O(log(n)) time complexity v total time complexity = O(n log(n)) v Pros: fast sorting algorithm, memory efficient, especially for very large values of n. v Cons: slower of the O(n log(n)) sorting algorithms