Heap structure Pasi Frnti Sami Sieranoja 21 10



![Heapsort(A[1, N]) 15 Heapify(A); FOR i N DOWNTO 2 DO Swap(A[1], A[i]); Sink(A, 1, Heapsort(A[1, N]) 15 Heapify(A); FOR i N DOWNTO 2 DO Swap(A[1], A[i]); Sink(A, 1,](https://slidetodoc.com/presentation_image_h/054f203176c99821203fc017cb7e7a8d/image-12.jpg)




![Heapsort Straightforward implementation Heapsort(A[1, N]) H Create. Heap(); O(1) FOR i 1 TO N Heapsort Straightforward implementation Heapsort(A[1, N]) H Create. Heap(); O(1) FOR i 1 TO N](https://slidetodoc.com/presentation_image_h/054f203176c99821203fc017cb7e7a8d/image-19.jpg)

- Slides: 22

Heap structure Pasi Fränti, Sami Sieranoja 21. 10. 2018

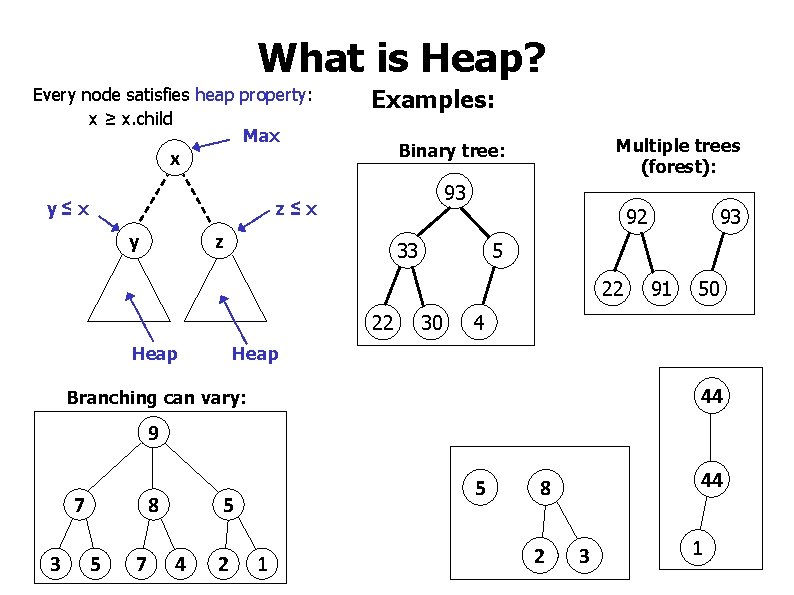
What is Heap? Every node satisfies heap property: x ≥ x. child Max Examples: y≤x 93 z≤x y Multiple trees (forest): Binary tree: x 92 z 33 5 22 22 Heap 93 30 91 50 4 Heap 44 Branching can vary: 9 7 3 8 5 7 5 5 4 2 1 44 8 2 3 1

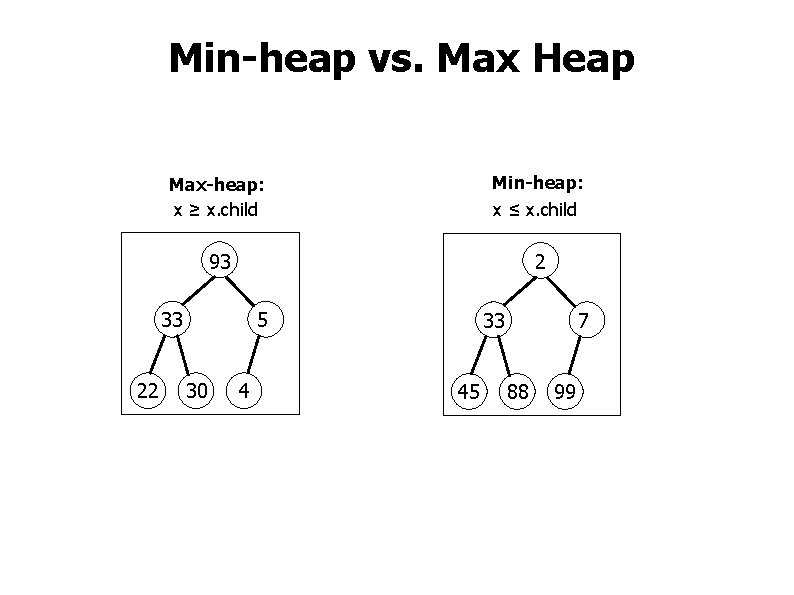
Min-heap vs. Max Heap Max-heap: x ≥ x. child Min-heap: 93 2 33 22 x ≤ x. child 5 30 4 33 45 7 88 99

Properties and use of (binary) heaps Creation: O(N) Insert: O(log N) Delete: O(log N) Find max: O(1) Quick access to Largest element 17 9 Usage: • Sorting • Priority queue • Find k largest elements 14 8 3 6 4 7 2 5 Always balanced Height = log(N) +1

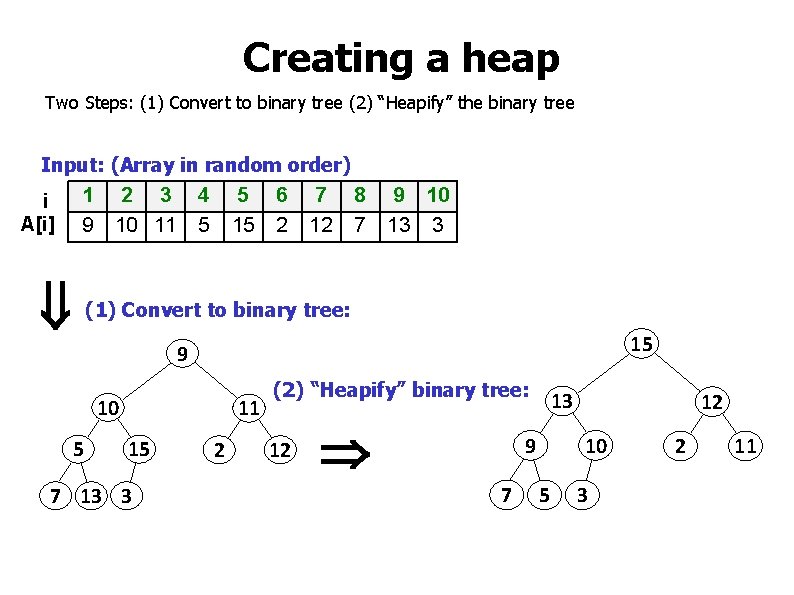
Creating a heap Two Steps: (1) Convert to binary tree (2) “Heapify” the binary tree Input: (Array in random order) i A[i] 1 9 2 3 10 11 4 5 5 15 6 2 7 12 8 7 9 10 13 3 (1) Convert to binary tree: 15 9 10 5 11 15 7 13 3 2 (2) “Heapify” binary tree: 12 13 9 7 12 10 5 3 2 11

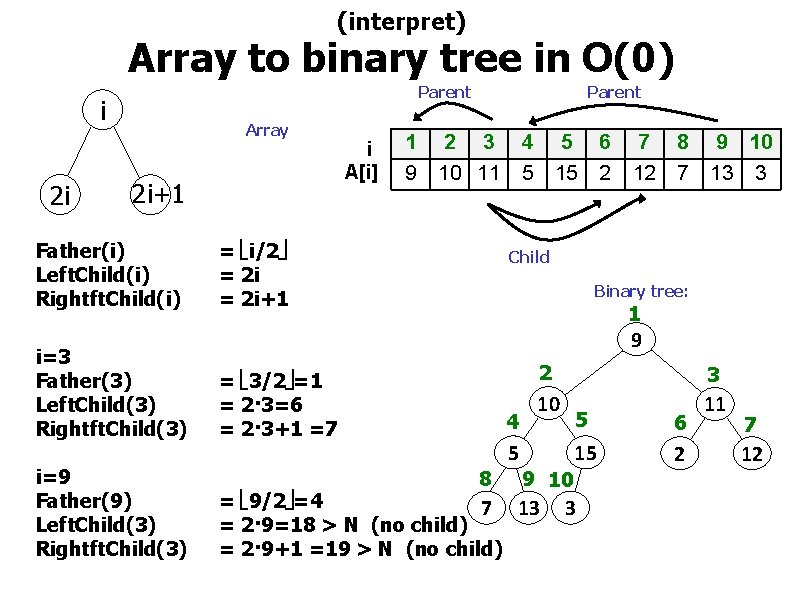
(interpret) Array to binary tree in O(0) Parent i 2 i Array 2 i+1 Father(i) Left. Child(i) Rightft. Child(i) i=3 Father(3) Left. Child(3) Rightft. Child(3) i=9 Father(9) Left. Child(3) Rightft. Child(3) i A[i] 1 9 Parent 2 3 10 11 = i/2 = 2 i+1 4 5 5 15 6 2 7 12 8 7 9 10 13 3 Child Binary tree: 1 9 = 3/2 =1 = 2· 3=6 = 2· 3+1 =7 4 8 5 2 3 10 11 9 10 = 9/2 =4 7 13 = 2· 9=18 > N (no child) = 2· 9+1 =19 > N (no child) 5 6 15 2 3 7 12

Sink and Sift-Up operations Operations on heap: • Heapify • Insert • Delete • Modify Depend on two operations: • Sink • Sift-Up

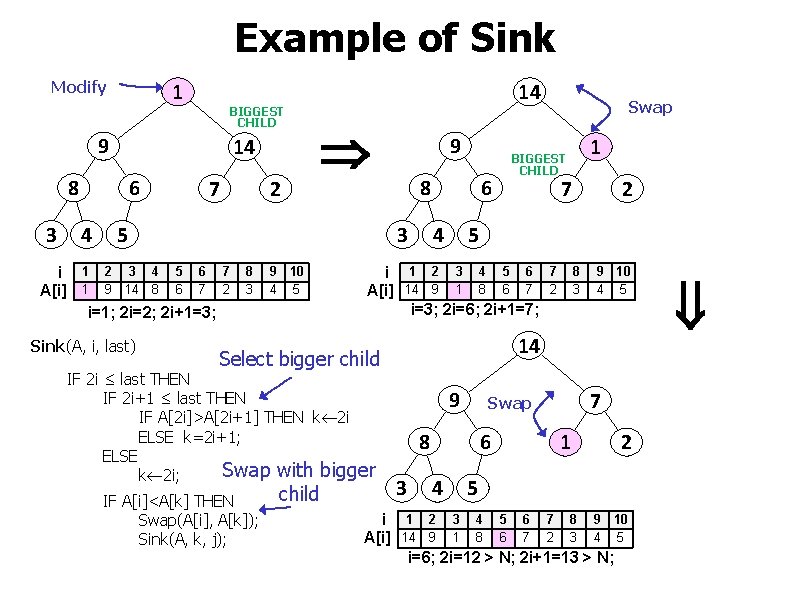
Example of Sink Modify 1 BIGGEST CHILD 9 14 8 3 6 4 7 2 14 5 8 3 9 10 4 5 6 4 child 2 5 8 3 9 10 4 5 14 Select bigger child IF A[i]<A[k] THEN Swap(A[i], A[k]); Sink(A, k, j); 7 i 1 2 3 4 5 6 7 A[i] 14 9 1 8 6 7 2 i=3; 2 i=6; 2 i+1=7; IF 2 i ≤ last THEN IF 2 i+1 ≤ last THEN IF A[2 i]>A[2 i+1] THEN k 2 i ELSE k=2 i+1; ELSE Swap with bigger k 2 i; 1 BIGGEST CHILD 9 8 3 6 4 7 Swap 1 2 5 i 1 2 3 4 5 6 7 8 9 10 A[i] 14 9 1 8 6 7 2 3 4 5 i=6; 2 i=12 > N; 2 i+1=13 > N; i 1 2 3 4 5 6 7 A[i] 1 9 14 8 6 7 2 i=1; 2 i=2; 2 i+1=3; Sink(A, i, last) 9 Swap

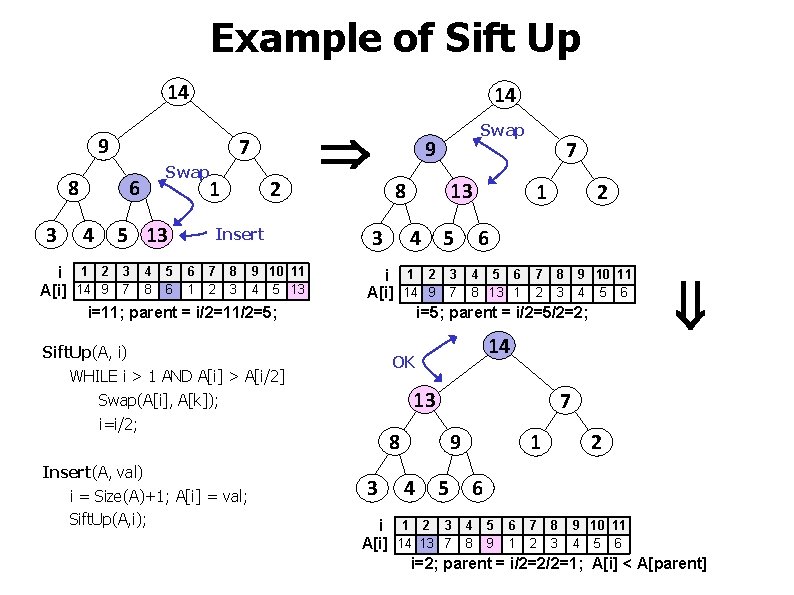
Example of Sift Up 14 14 9 8 3 7 6 4 Swap 5 13 1 2 Insert 9 8 3 4 5 1 2 6 i 1 2 3 4 5 6 7 8 9 10 11 A[i] 14 9 7 8 13 1 2 3 4 5 6 i=5; parent = i/2=5/2=2; Sift. Up(A, i) WHILE i > 1 AND A[i] > A[i/2] Swap(A[i], A[k]); i=i/2; Insert(A, val) i = Size(A)+1; A[i] = val; Sift. Up(A, i); 13 7 14 OK 13 7 8 3 9 4 i 1 2 3 4 5 6 7 8 9 10 11 A[i] 14 9 7 8 6 1 2 3 4 5 13 i=11; parent = i/2=11/2=5; Swap 5 1 2 6 i 1 2 3 4 5 6 7 8 9 10 11 A[i] 14 13 7 8 9 1 2 3 4 5 6 i=2; parent = i/2=2/2=1; A[i] < A[parent]

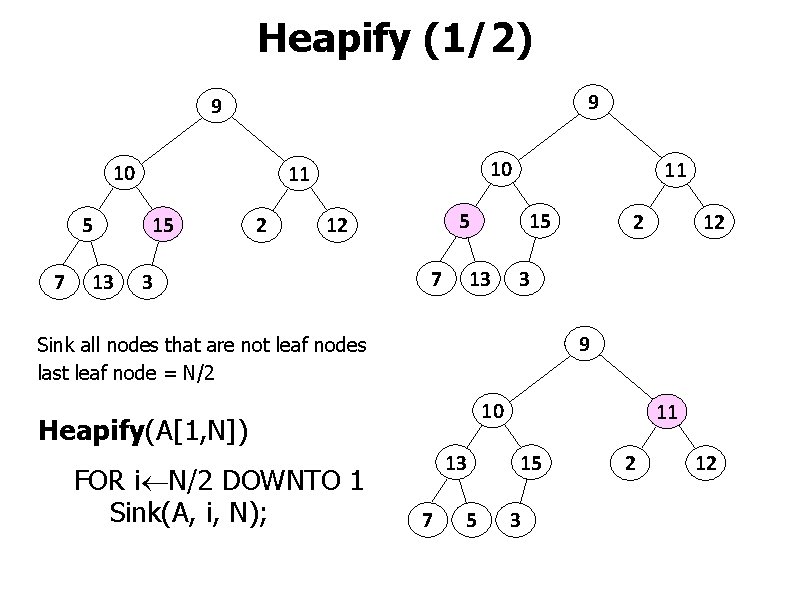
Heapify (1/2) 9 9 10 5 7 13 10 11 15 2 5 12 3 11 7 15 13 12 3 9 Sink all nodes that are not leaf nodes last leaf node = N/2 10 Heapify(A[1, N]) FOR i N/2 DOWNTO 1 Sink(A, i, N); 2 13 7 5 11 15 3 2 12

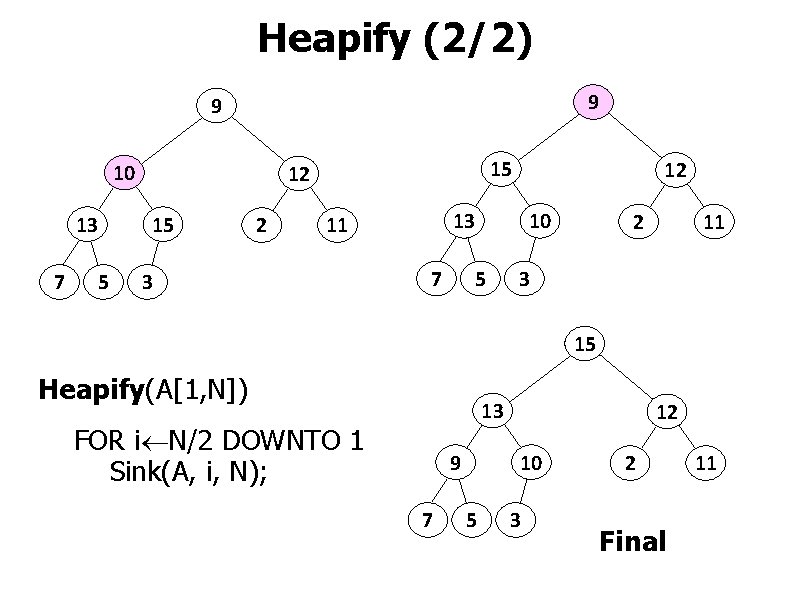
Heapify (2/2) 9 9 10 13 7 5 15 12 15 2 13 11 3 12 7 10 5 2 11 3 15 Heapify(A[1, N]) 13 FOR i N/2 DOWNTO 1 Sink(A, i, N); 9 7 12 10 5 3 2 Final 11
![HeapsortA1 N 15 HeapifyA FOR i N DOWNTO 2 DO SwapA1 Ai SinkA 1 Heapsort(A[1, N]) 15 Heapify(A); FOR i N DOWNTO 2 DO Swap(A[1], A[i]); Sink(A, 1,](https://slidetodoc.com/presentation_image_h/054f203176c99821203fc017cb7e7a8d/image-12.jpg)
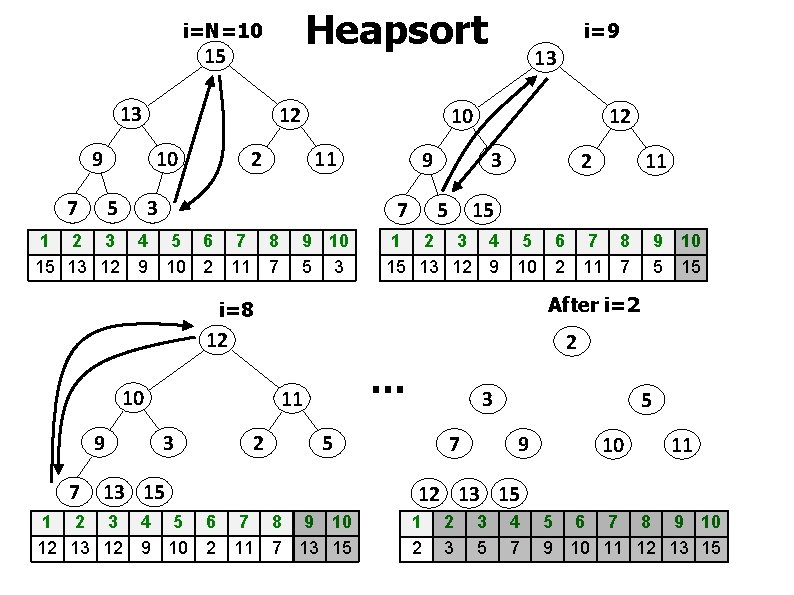
Heapsort(A[1, N]) 15 Heapify(A); FOR i N DOWNTO 2 DO Swap(A[1], A[i]); Sink(A, 1, i-1); 13 9 7 12 10 5 3 2 11

Heapsort i=N=10 15 13 9 7 12 10 5 13 10 2 11 3 9 10 5 3 12 9 7 1 2 3 4 5 6 7 8 15 13 12 9 10 2 11 7 i=9 3 5 2 15 1 2 3 4 5 6 7 8 15 13 12 9 10 2 11 7 12 2 10 7 … 11 3 9 10 5 15 After i=2 i=8 9 11 2 3 5 13 15 1 2 3 4 5 6 7 8 9 10 12 13 12 9 10 2 11 7 13 15 7 5 9 10 11 12 13 15 1 2 2 3 3 5 4 7 5 6 7 8 9 10 11 12 13 15

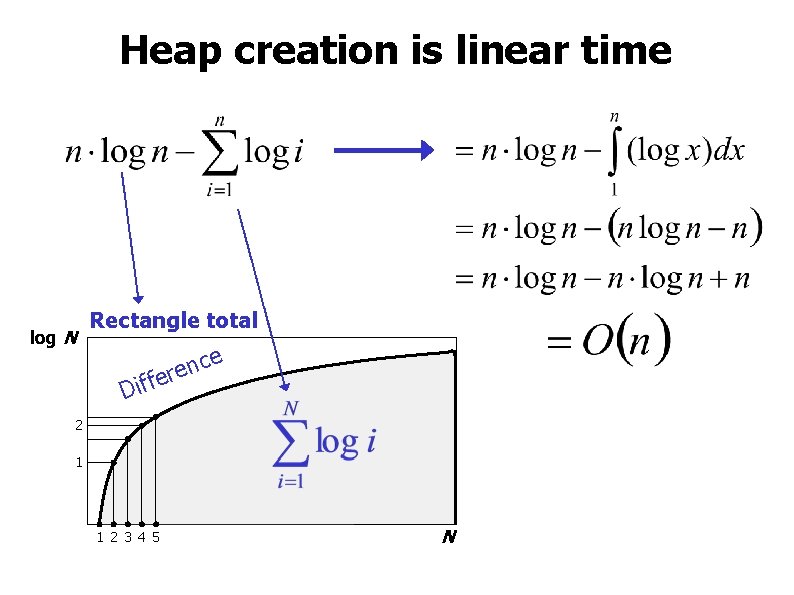
Heap creation is linear time • • • Half of the elements need no work Next half only one level Element at location i needs (logn - logi) work i Sink(i, n) n

Heap creation is linear time log N Rectangle total ce n e fer Dif 2 1 1 2 3 4 5 N

Empty space for notes

Empty space for notes

Extra slides
![Heapsort Straightforward implementation HeapsortA1 N H Create Heap O1 FOR i 1 TO N Heapsort Straightforward implementation Heapsort(A[1, N]) H Create. Heap(); O(1) FOR i 1 TO N](https://slidetodoc.com/presentation_image_h/054f203176c99821203fc017cb7e7a8d/image-19.jpg)
Heapsort Straightforward implementation Heapsort(A[1, N]) H Create. Heap(); O(1) FOR i 1 TO N DO Insert(H, A[i]); O(N log. N) FOR i N DOWNTO 1 DO A[i] Remove. Max(); O(N log. N) 7 4 6 1 8 … 1 4 6 7 8 … Insert Remove Requires O(N) extra space for the heap

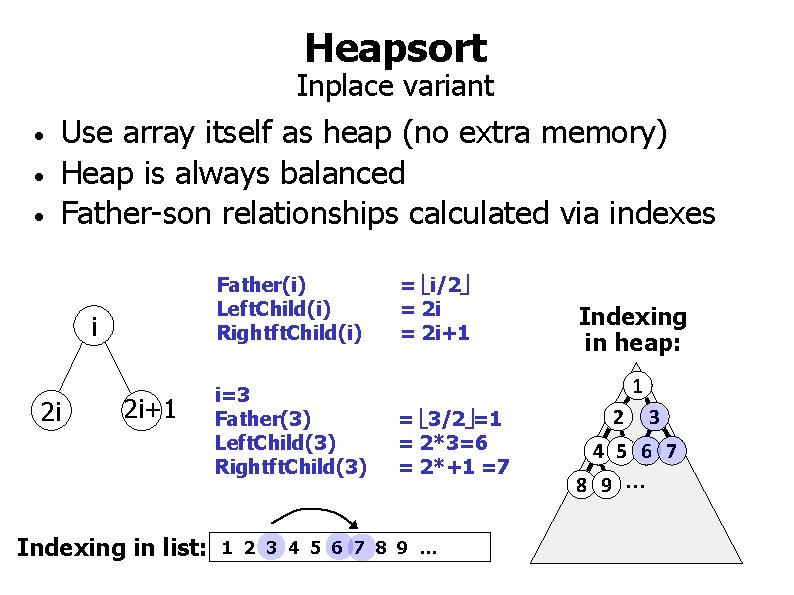
Heapsort Inplace variant • • • Use array itself as heap (no extra memory) Heap is always balanced Father-son relationships calculated via indexes Father(i) Left. Child(i) Rightft. Child(i) i 2 i 2 i+1 Indexing in list: i=3 Father(3) Left. Child(3) Rightft. Child(3) = i/2 = 2 i+1 Indexing in heap: 1 = 3/2 =1 = 2*3=6 = 2*+1 =7 1 2 3 4 5 6 7 8 9 …

Sink function Sink(A, i, j) Left child exists Right child exists IF 2 i ≤ j THEN IF 2 i+1 ≤ j THEN IF A[2 i]>A[2 i+1] THEN k 2 i ELSE k=2 i+1; ELSE Select bigger child k 2 i; IF A[i]<A[k] THEN Swap(A[i], A[k]); Sink(A, k, j); Swap if needed Sink recursively

Ju st Another example ba ck -u p 100 93 74 92 22 93 91 22 67 35 43 65 5 27 17