Heap Sort The heap is used in an

Heap Sort The heap is used in an elegant sorting algorithm called heap sort. Suppose H is a complete binary tree with n elements. (assume that H is maintained in memory by a linear array TREE using the sequential representation of H, not a linked representation. ) then H is called a heap, or a max heap, if each node N of H has the following property: the value at N is greater than or equal to the value at any of the children of N. accordingly, the value at N is greater than or equal to the value at any of the descendants of N. (A minheap is defined analogously: the value at N is less than or equal to the value at any of the children of N. )

n n n Example Consider the complete tree H in fig 1(a). observe that H is a heap. This means, in particular, that the largest element in H appears at the “top” of the heap, that is, at the root of the tree. Fig 1(b) shows the sequential representation of H by the array TREE. That is, TREE[1] is the root of the tree H, and the left and right children of node TREE[K] are, respectively, TREE[2 K] and TREE[2 K+1]. This means, in particular, that the parent of any nontoot node TREE[J] is the node TREE[J÷ 2](where J ÷ 2 means integer division). Observe that the node of H on the same level appear one after the other in the array TREE.

n Example 97 95 88 95 66 66 18 48 55 62 35 48 40 30 26 55 24 77 25 38

n n Example Suppose we want to build a heap H from the following list of numbers: this we can be accomplished by inserting the eight numbers one after the other into an empty heap H using the above procedure. 2(a) through (h) shows the respective pictures of the heap after each of the eight elements has been inserted. Again, the dotted line indicates that an exchange has taken place during the insertion of the given item of the information. 44 44 30 50 44 30 22 44

n example 60 60 50 22 50 44 22 30 77 55 30 44 50 22 60 30 44 55

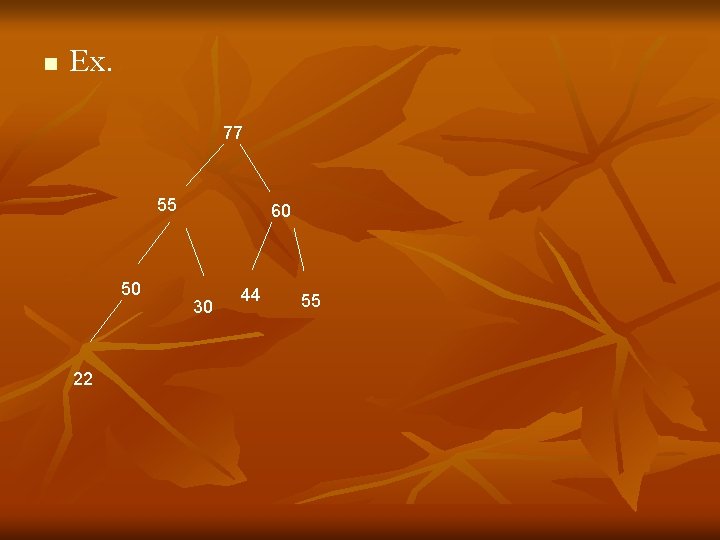
n Ex. 77 55 50 22 60 30 44 55

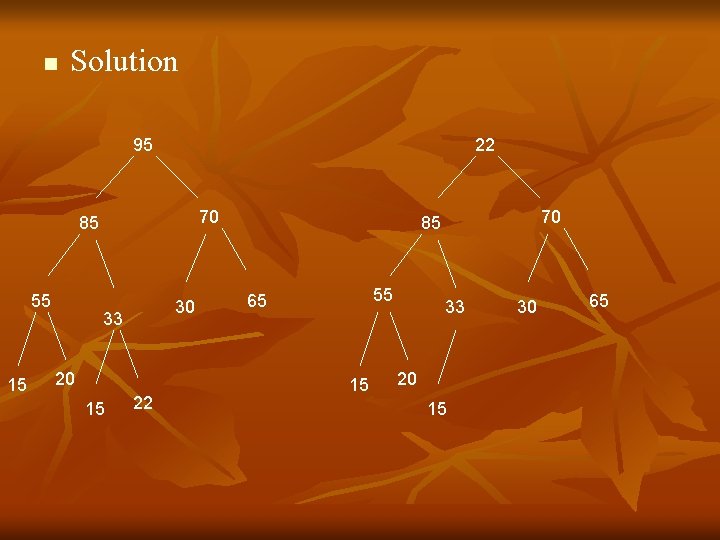
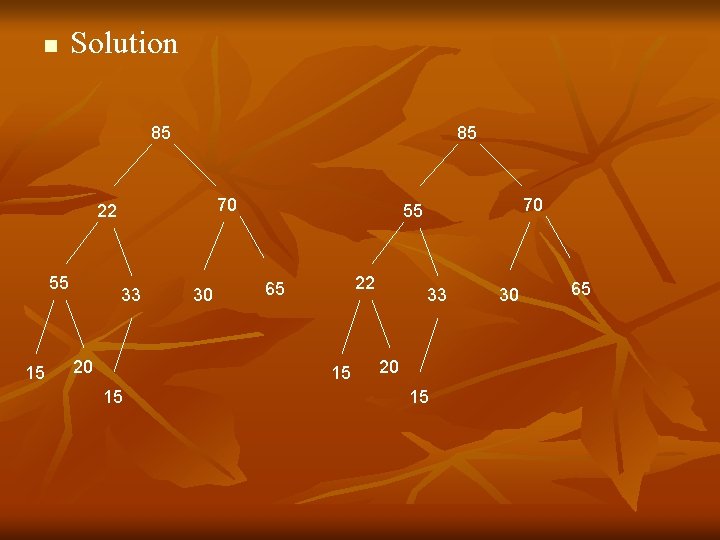
n n Example consider the heap H in fig 3(a), where R=95 is the root and L=22 is the last node of the tree. Step 1 of the above procedure deletes R=95, and step 2 replaces R =95 by L =22. this gives the complete tree in fir 3(b), whivn is not a heap. Observe , however that both the right and left sub tree of 222 are still heaps. Applying Step 3 we find appropriate place of 22 in the heap as follows: (a) compare 22 with its two children, 85 and 70. since 22 is less than the larger child, 85, interchange 22 and 85 so the tree now looks like fig 3©. (b) compare 22 with its two new children, 55 and 33. since 22 is less than the larger child, 55, interchange 22 and 55 so the tree now looks like fig 3(d). ©compare 22 with its new children, 15 and 20. since 22 is greater than the both children, node 22 has dropped to its appropriate place in H.

n Solution 95 22 70 85 55 15 30 33 20 15 22 70 85 55 65 15 33 20 15 30 65

n Solution 85 85 70 22 55 15 33 20 30 22 65 15 15 70 55 33 20 15 30 65