Heap Sort Overview Uses a heap as its





- Slides: 12

Heap Sort Overview: Uses a heap as its data structure In-place sorting algorithm – memory efficient Time complexity – O(n log(n))

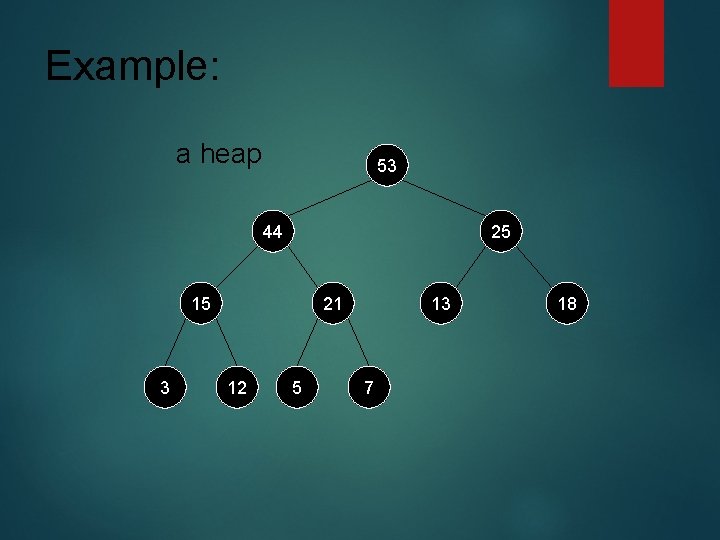
What is a Heap? A heap is also known as a priority queue and can be represented by a binary tree with the following properties: Structure property: A heap is a completely filled binary tree with the exception of the bottom row, which is filled from left to right Heap Order property: For every node x in the heap, the parent of x greater than or equal to the value of x. (known as a max. Heap).

Example: a heap 53 44 25 15 3 21 12 5 13 7 18

Algorithm Step 1. Build Heap – O(n) - Build binary tree taking N items as input, ensuring the heap structure property is held, in other words, build a complete binary tree. - Heapify the binary tree making sure the binary tree satisfies the Heap Order property. Step 2. Perform n delete. Max operations – O(log(n)) - Delete the maximum element in the heap – which is the root node, and place this element at the end of the sorted array.

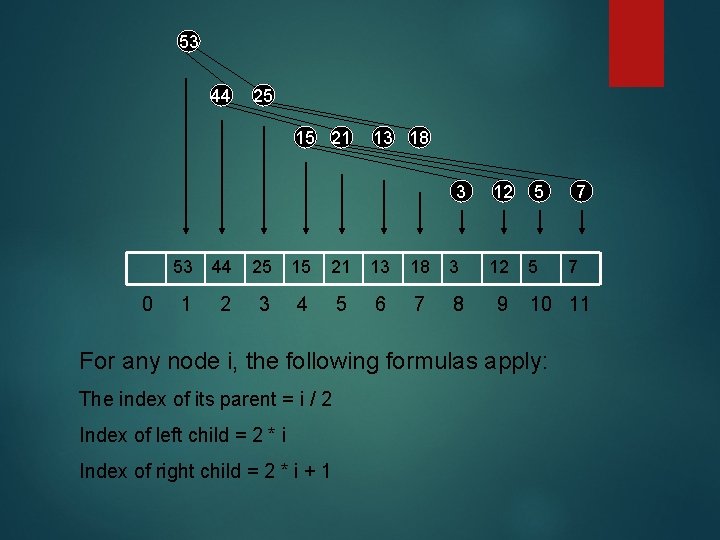
Simplifying things For speed and efficiency we can represent the heap with an array. Place the root at array index 1, its left child at index 2, its right child at index 3, so on and so forth… 53 44 25 15 21 13 18 3 0 12 53 44 25 15 21 13 18 3 12 1 2 3 4 5 6 7 8 9 5 5 7 7 10 11

53 44 25 15 21 13 18 3 0 12 53 44 25 15 21 13 18 3 12 1 2 3 4 5 6 7 8 9 5 5 Index of left child = 2 * i Index of right child = 2 * i + 1 7 10 11 For any node i, the following formulas apply: The index of its parent = i / 2 7

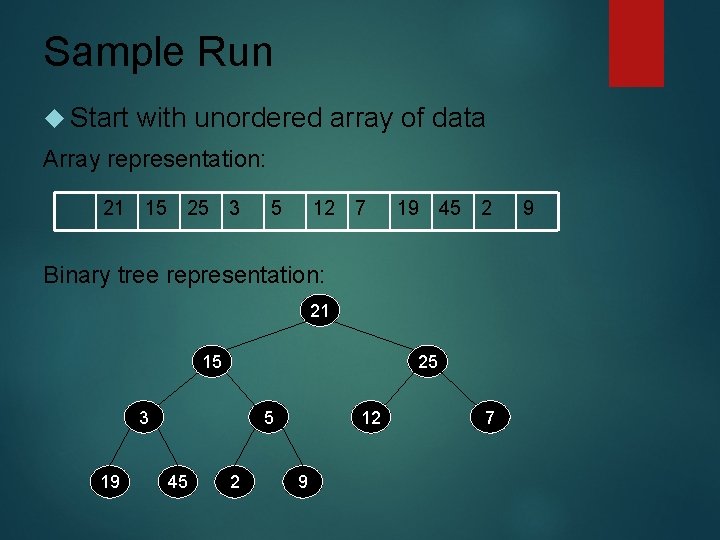
Sample Run Start with unordered array of data Array representation: 21 15 25 3 5 12 7 19 45 2 Binary tree representation: 21 15 25 3 19 5 45 2 12 9 7 9

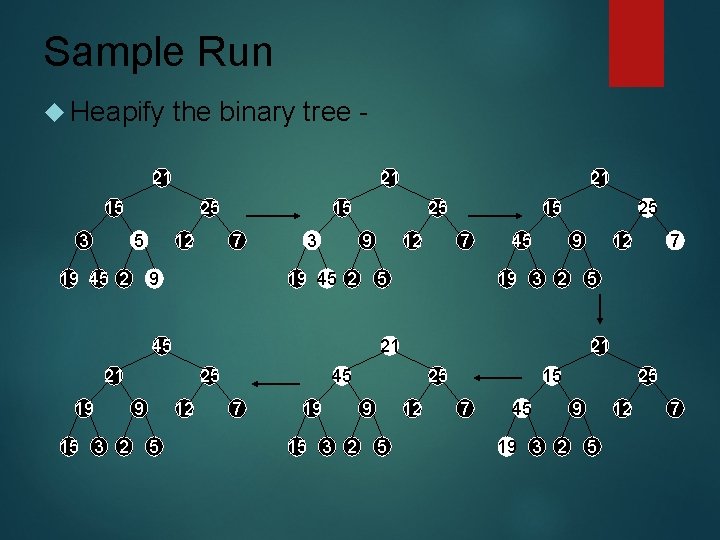
Sample Run Heapify the binary tree - 21 21 15 3 25 5 19 45 2 12 15 7 9 3 25 9 19 45 2 15 3 2 25 12 5 7 45 25 9 19 3 2 19 15 3 2 25 9 12 5 7 21 45 7 12 5 21 21 9 12 15 5 45 19 21 15 7 45 19 3 2 25 9 12 5 7

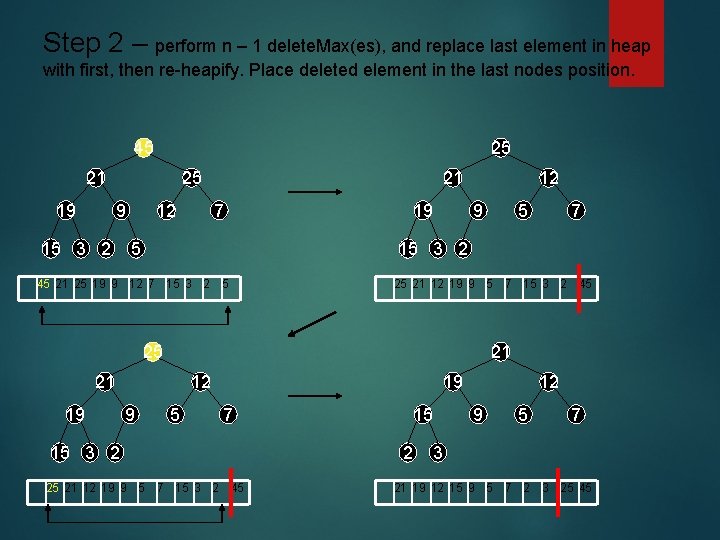
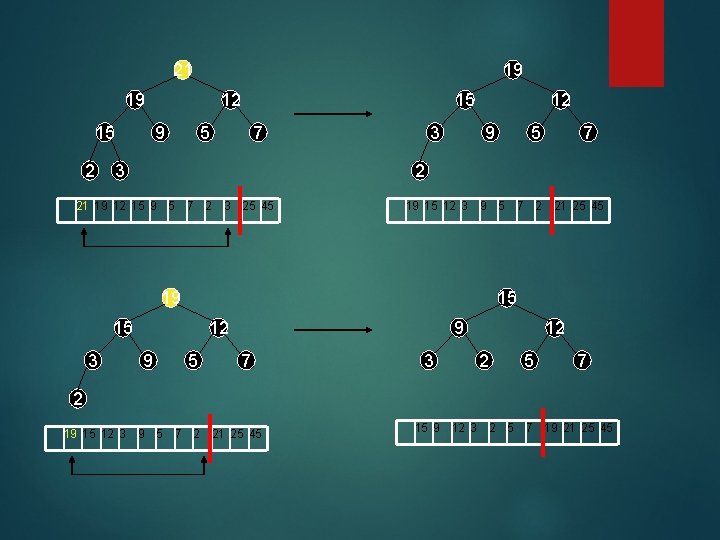
Step 2 – perform n – 1 delete. Max(es), and replace last element in heap with first, then re-heapify. Place deleted element in the last nodes position. 45 25 21 19 25 9 15 3 2 12 21 7 19 12 9 25 21 12 19 9 5 7 15 3 2 45 25 21 21 12 9 7 15 3 2 5 45 21 25 19 9 12 7 15 3 2 5 19 5 5 19 7 15 3 2 25 21 12 19 9 5 7 15 3 2 45 15 2 12 9 5 7 3 21 19 12 15 9 5 7 2 3 25 45

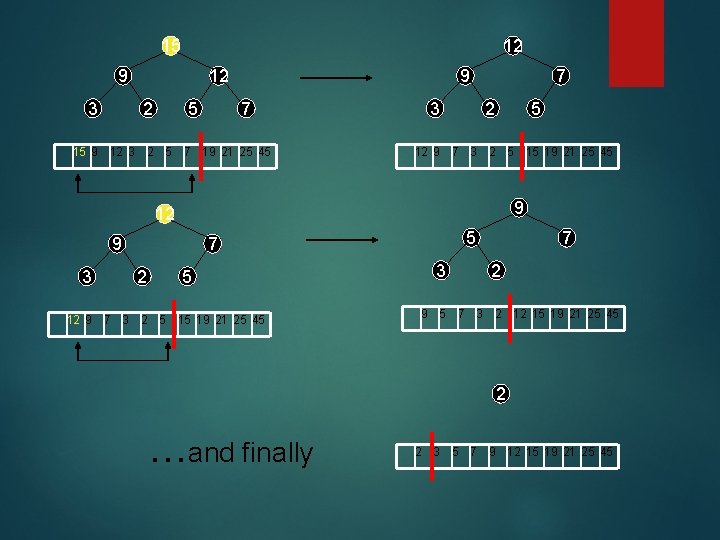
21 19 19 15 2 12 9 15 5 7 3 3 12 9 7 2 21 19 12 15 9 5 7 2 3 25 45 19 15 12 3 9 5 7 2 21 25 45 19 15 15 3 5 12 9 5 9 7 3 12 2 5 7 2 19 15 12 3 9 5 7 2 21 25 45 15 9 12 3 2 5 7 19 21 25 45

15 12 9 3 12 2 5 9 7 15 9 12 3 2 5 7 19 21 25 45 3 7 2 5 12 9 7 3 2 5 15 19 21 25 45 9 12 9 3 5 7 2 5 12 9 7 3 2 5 15 19 21 25 45 3 7 2 9 5 7 3 2 12 15 19 21 25 45 2 …and finally 2 3 5 7 9 12 15 19 21 25 45

Conclusion 1 st Step- Build heap, O(n) time complexity 2 nd Step – perform n delete. Max operations, each with O(log(n)) time complexity total time complexity = O(n log(n)) Pros: fast sorting algorithm, memory efficient, especially for very large values of n. Cons: slower of the O(n log(n)) sorting algorithms