Heap Sort CS 105 100205 Using a heap

Heap Sort CS 105 10/02/05

Using a heap to sort n Using a heap-based priority queue, sorting can be done in O( n log n ) time n n Insert all n elements in the priority queue Repeatedly remove the elements from the priority queue (they will come out sorted) 2 n operations on the priority queue, each taking O( log n ) time => O( n log n ) Sorting can be done within the array by treating the array as a heap Heap. Sort Slide 10/02/05

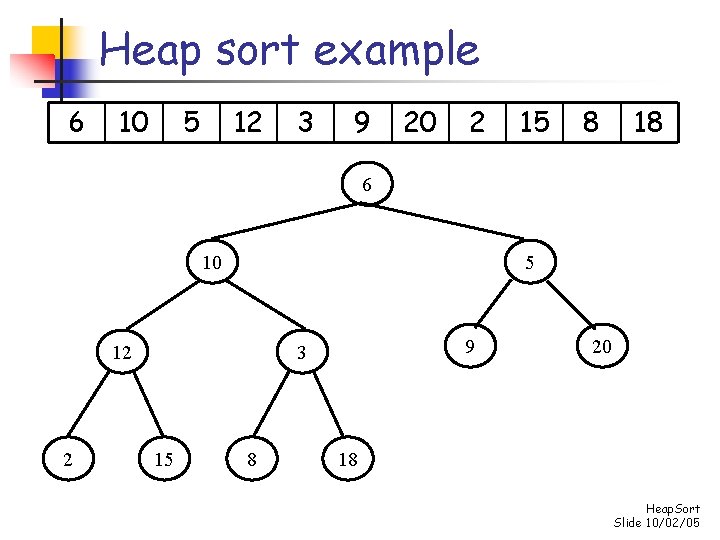
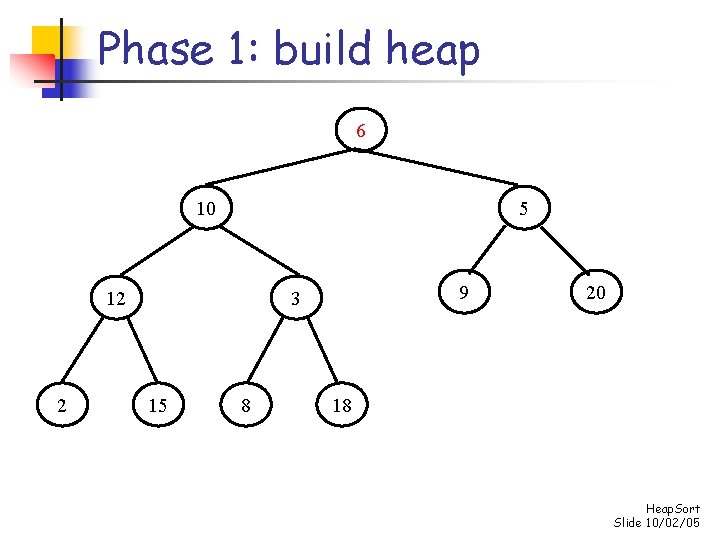
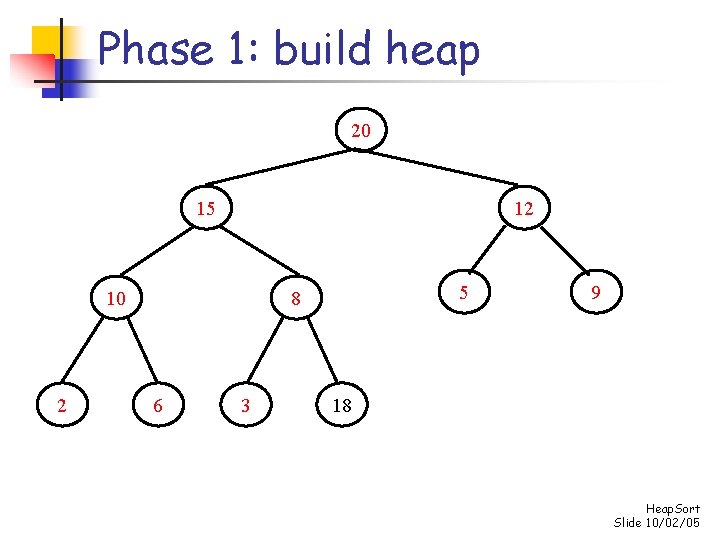
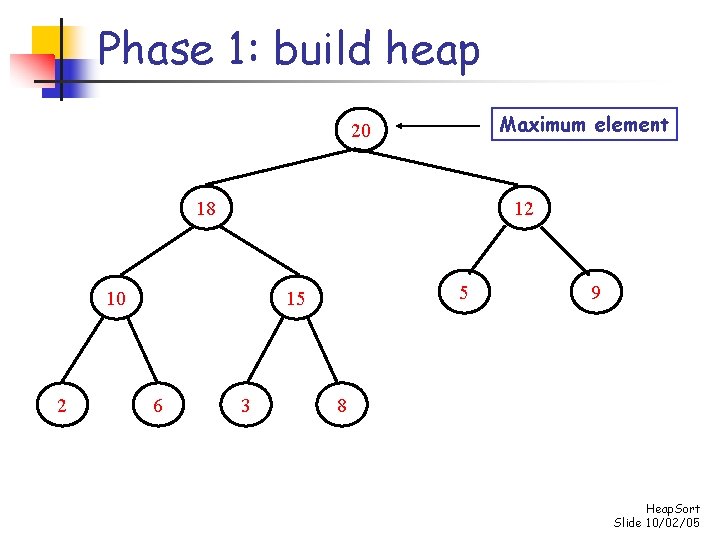
Heap sort n n n Reverse the heap property: child nodes should always be less than the parent nodes Phase 1: convert the array into an n-element heap Phase 2: repeatedly remove maximum element from the heap, and place that element in its proper position in the array n n swap element at 0 th position with element at (n-1)th position and then “reheapify” considering only the first n-1 elements repeat this process until heap size is reduced to 1 (minimum element remains, at 0 th position) Heap. Sort Slide 10/02/05

Heap sort example 6 10 5 12 3 9 20 2 15 8 18 6 10 5 12 2 9 3 15 8 20 18 Heap. Sort Slide 10/02/05

Phase 1: build the heap for i 1 to n-1 do insert element s[i] into the heap consisting of the elements s[0]…s[i-1] - Once the heap is built, s[0] will contain the maximum element Heap. Sort Slide 10/02/05

Phase 1: build heap 6 10 5 12 2 9 3 15 8 20 18 Heap. Sort Slide 10/02/05

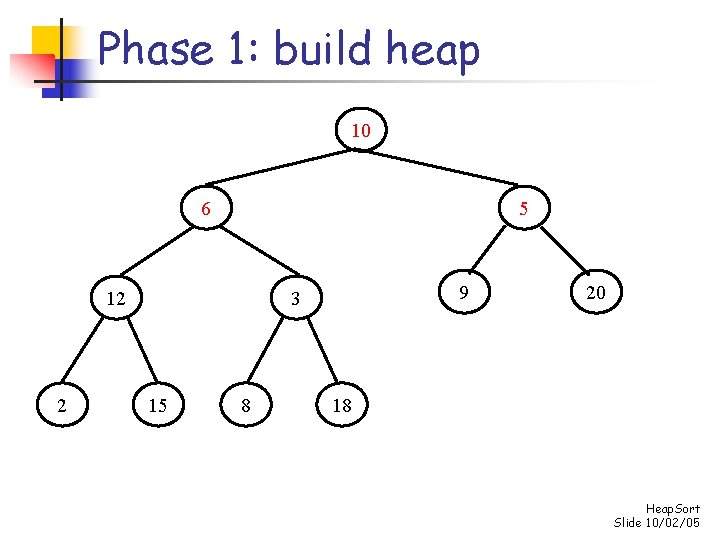
Phase 1: build heap 10 6 5 12 2 9 3 15 8 20 18 Heap. Sort Slide 10/02/05

Phase 1: build heap 10 6 5 12 2 9 3 15 8 20 18 Heap. Sort Slide 10/02/05

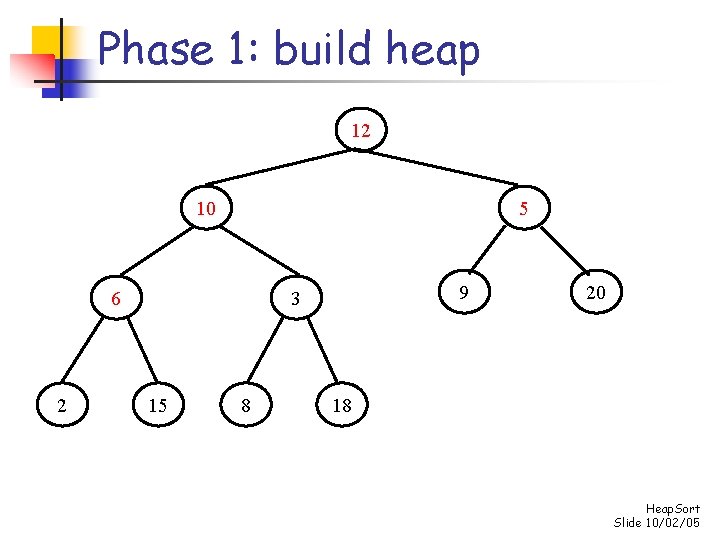
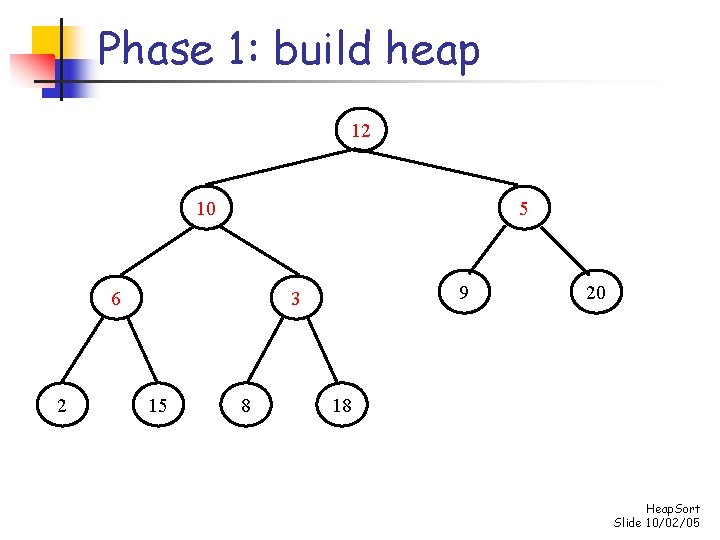
Phase 1: build heap 12 10 5 6 2 9 3 15 8 20 18 Heap. Sort Slide 10/02/05

Phase 1: build heap 12 10 5 6 2 9 3 15 8 20 18 Heap. Sort Slide 10/02/05

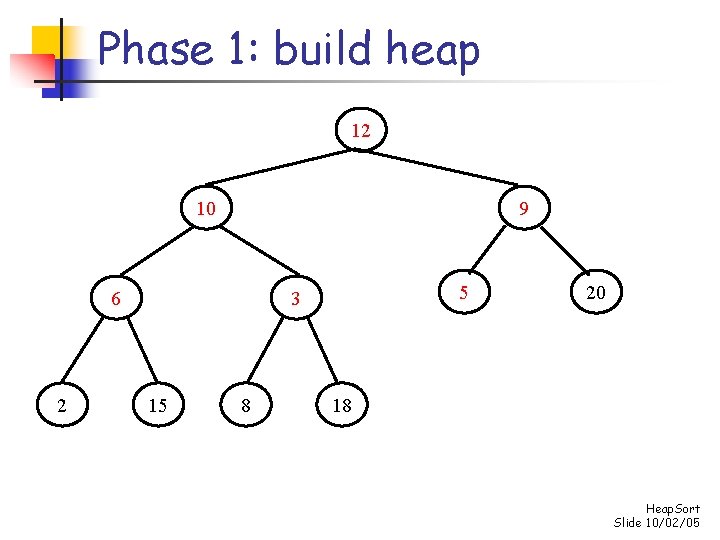
Phase 1: build heap 12 10 9 6 2 5 3 15 8 20 18 Heap. Sort Slide 10/02/05

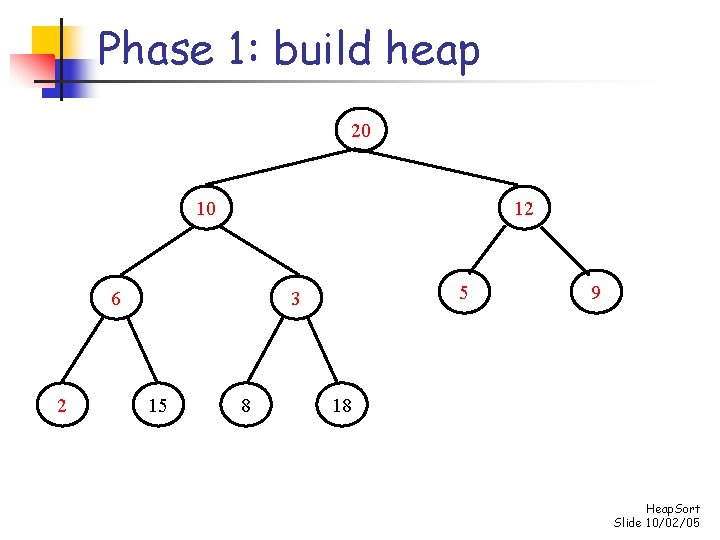
Phase 1: build heap 20 10 12 6 2 5 3 15 8 9 18 Heap. Sort Slide 10/02/05

Phase 1: build heap 20 10 12 6 2 5 3 15 8 9 18 Heap. Sort Slide 10/02/05

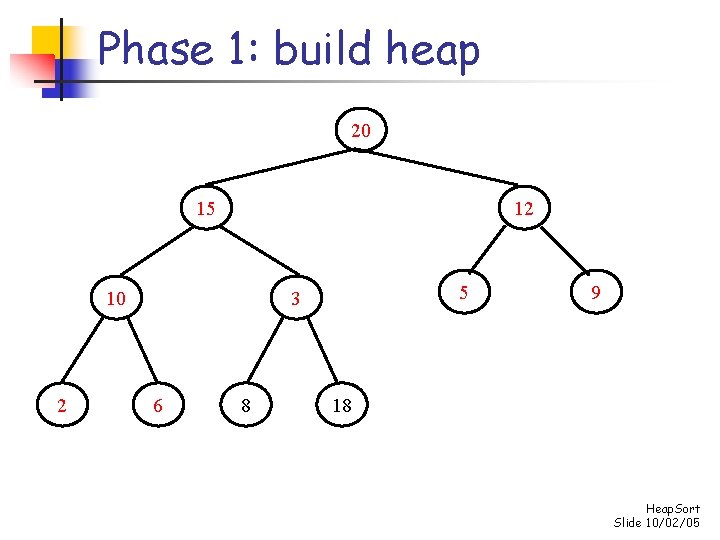
Phase 1: build heap 20 15 12 10 2 5 3 6 8 9 18 Heap. Sort Slide 10/02/05

Phase 1: build heap 20 15 12 10 2 5 8 6 3 9 18 Heap. Sort Slide 10/02/05

Phase 1: build heap Maximum element 20 18 12 10 2 5 15 6 3 9 8 Heap. Sort Slide 10/02/05

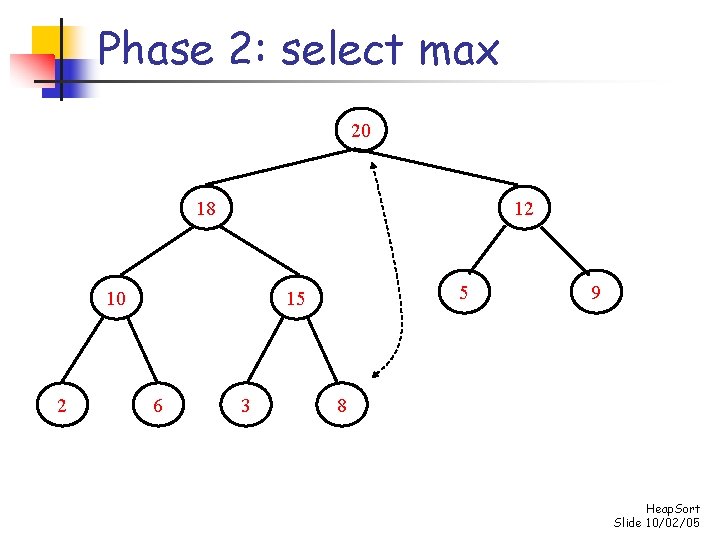
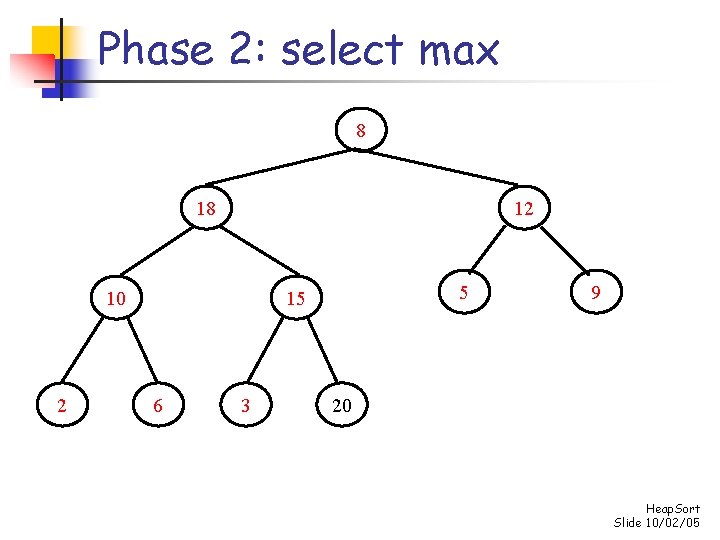
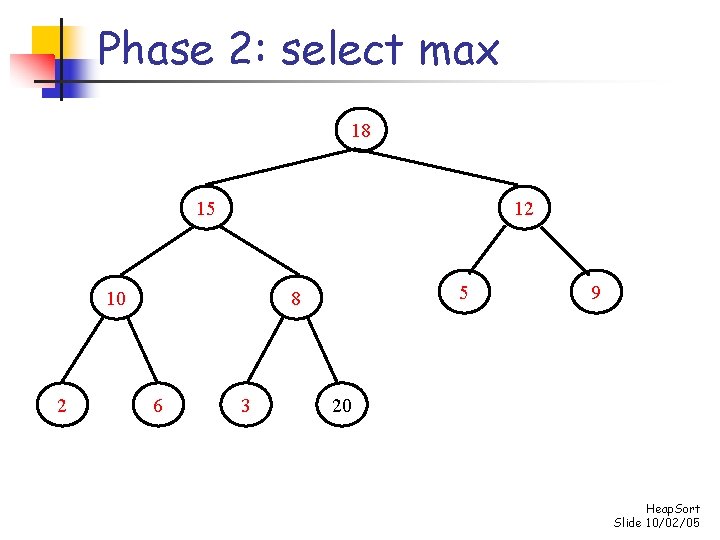
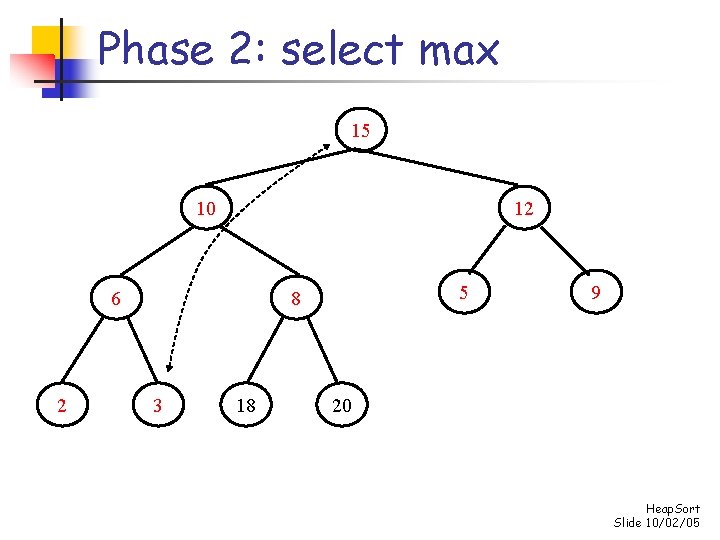
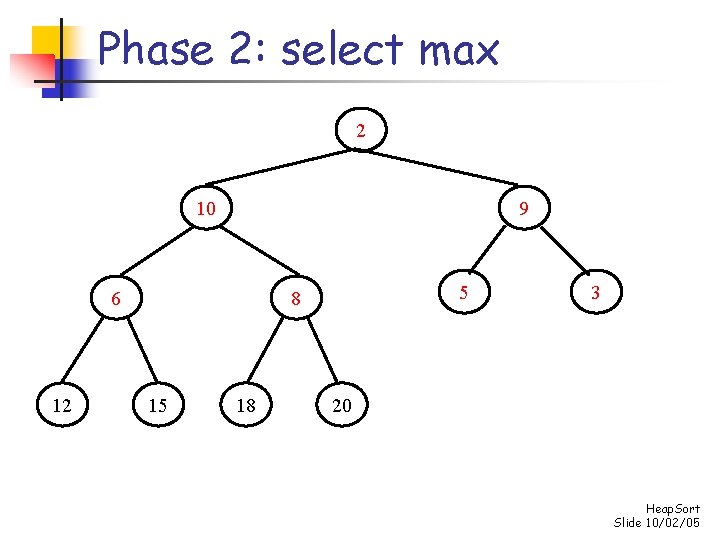
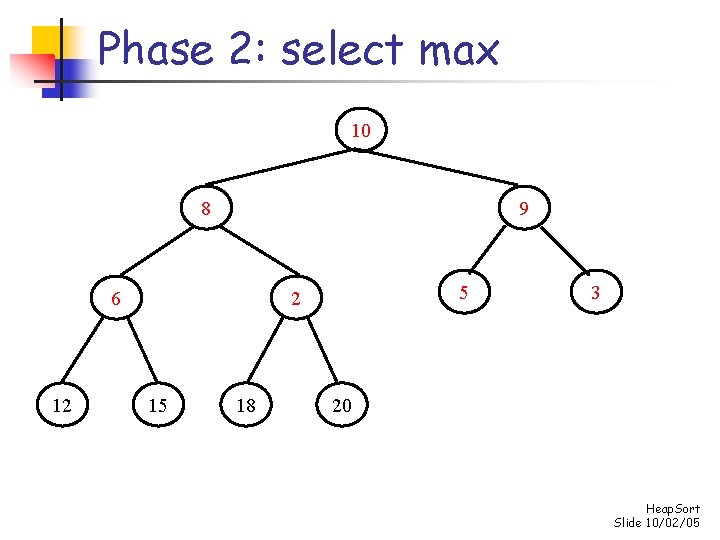
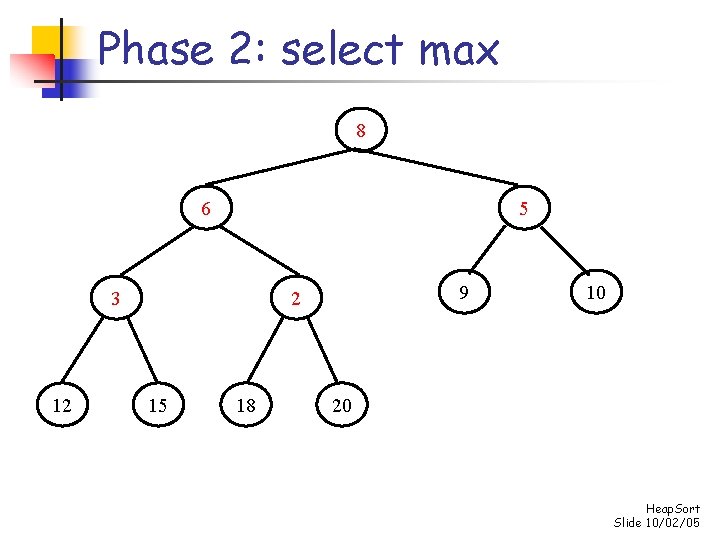
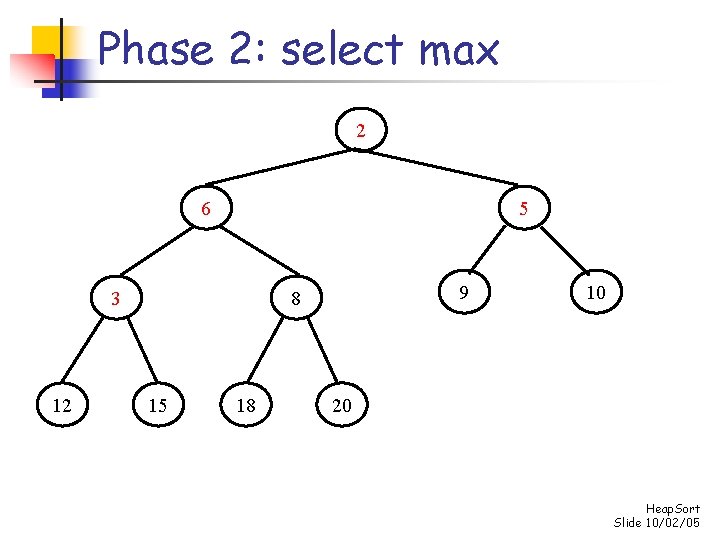
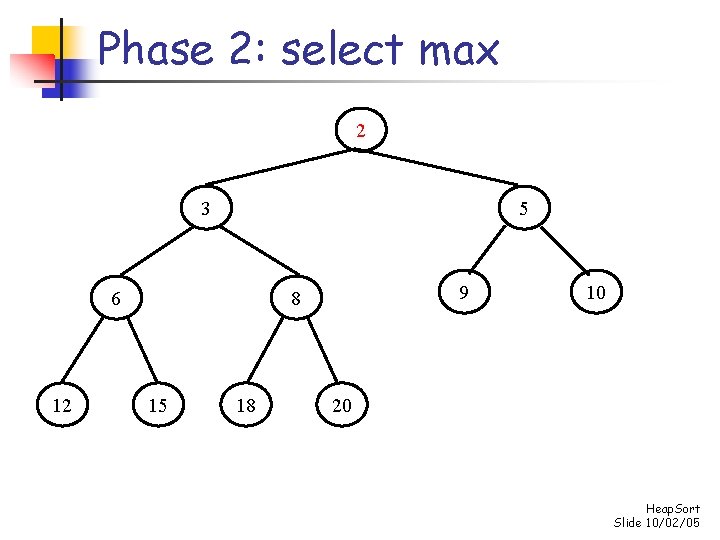
Phase 2: repeatedly select max for i n-1 down to 1 do swap s[0] and s[i] “demote” s[0] to its proper place in the heap consisting of the elements s[0]. . . s[i-1] Heap. Sort Slide 10/02/05

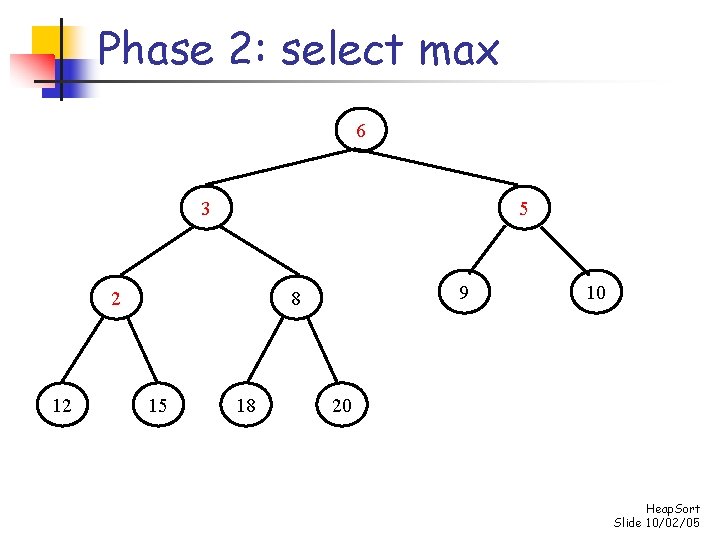
Phase 2: select max 20 18 12 10 2 5 15 6 3 9 8 Heap. Sort Slide 10/02/05

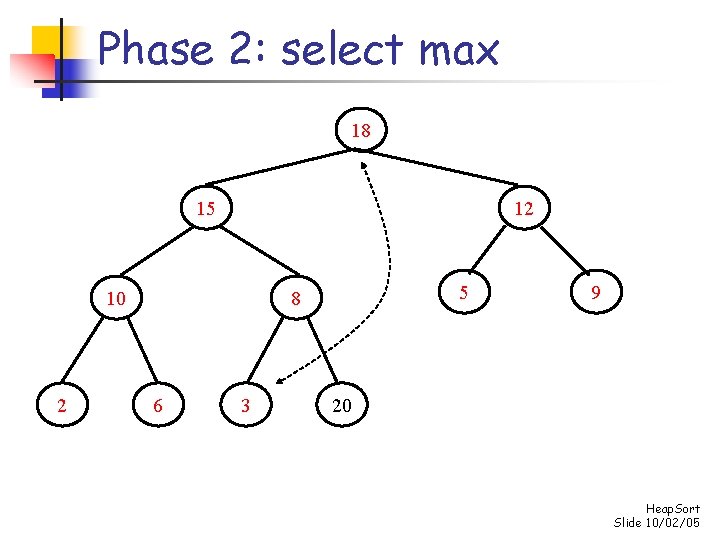
Phase 2: select max 8 18 12 10 2 5 15 6 3 9 20 Heap. Sort Slide 10/02/05

Phase 2: select max 18 15 12 10 2 5 8 6 3 9 20 Heap. Sort Slide 10/02/05

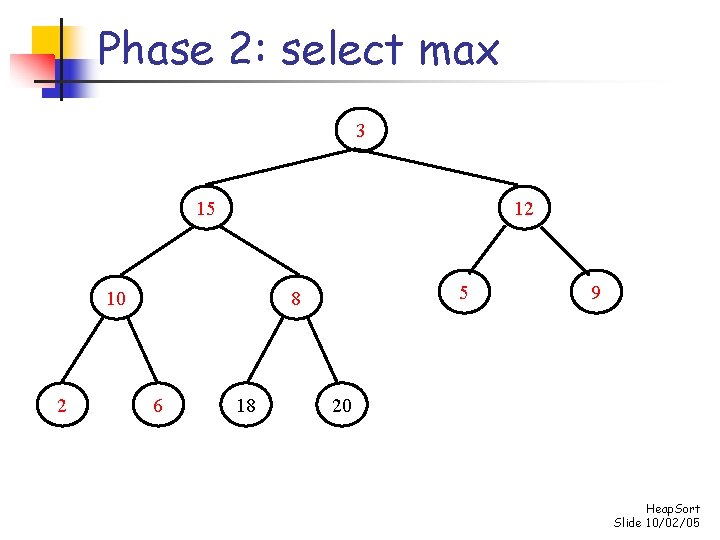
Phase 2: select max 18 15 12 10 2 5 8 6 3 9 20 Heap. Sort Slide 10/02/05

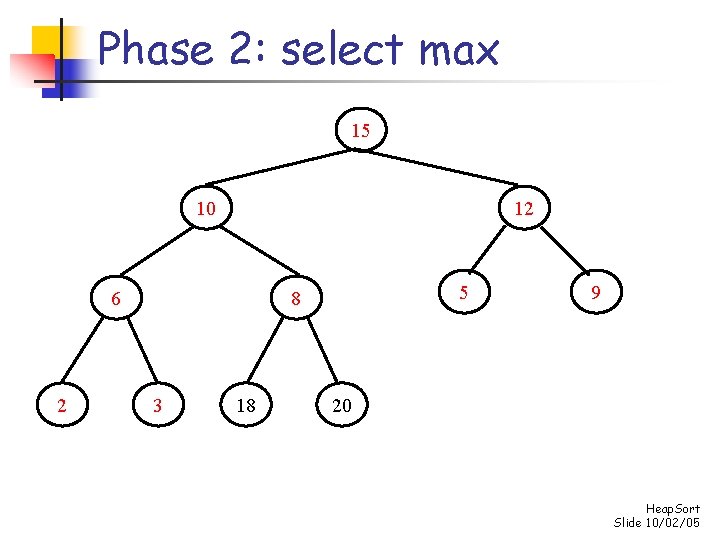
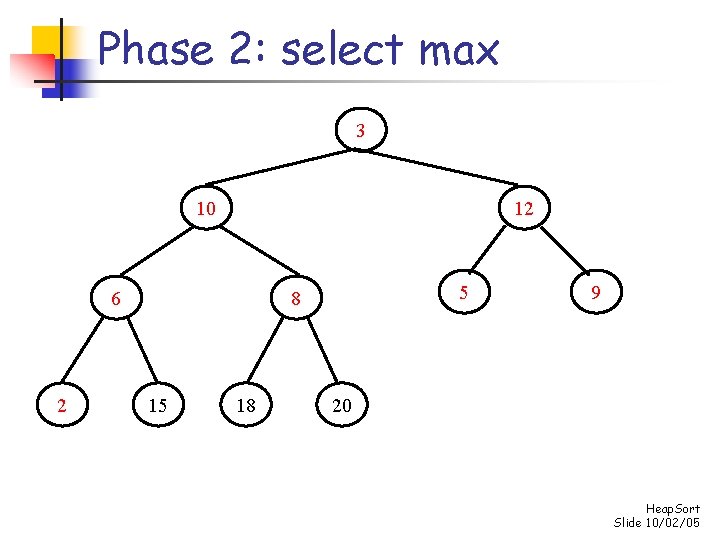
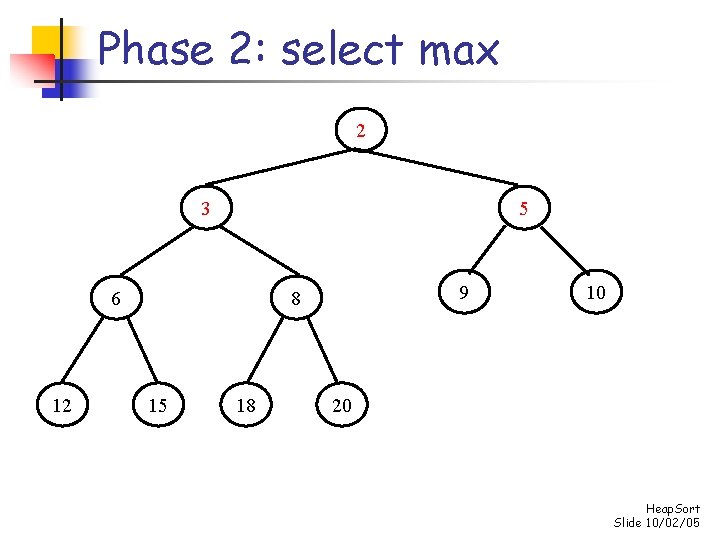
Phase 2: select max 3 15 12 10 2 5 8 6 18 9 20 Heap. Sort Slide 10/02/05

Phase 2: select max 15 10 12 6 2 5 8 3 18 9 20 Heap. Sort Slide 10/02/05

Phase 2: select max 15 10 12 6 2 5 8 3 18 9 20 Heap. Sort Slide 10/02/05

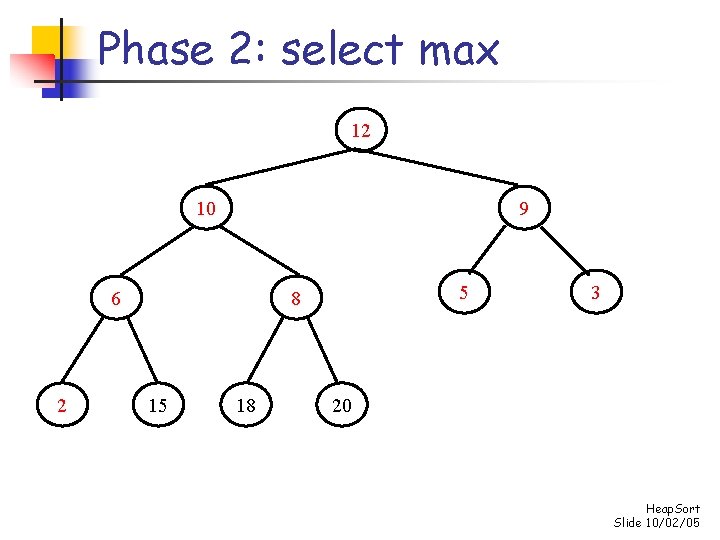
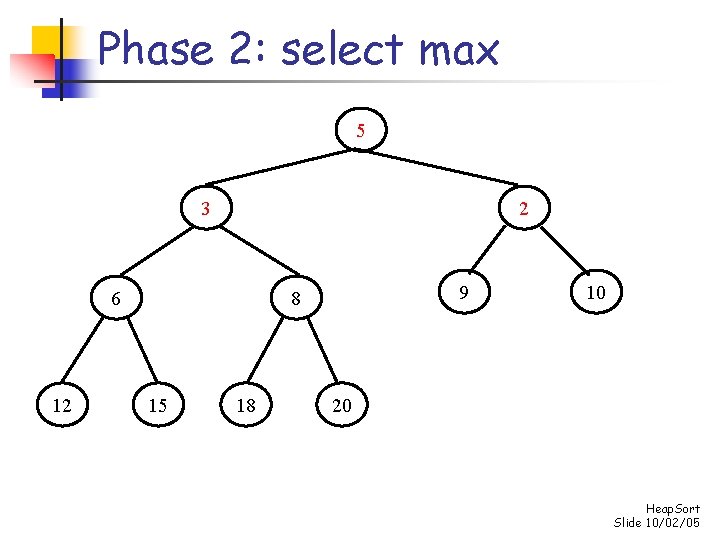
Phase 2: select max 3 10 12 6 2 5 8 15 18 9 20 Heap. Sort Slide 10/02/05

Phase 2: select max 12 10 9 6 2 5 8 15 18 3 20 Heap. Sort Slide 10/02/05

Phase 2: select max 12 10 9 6 2 5 8 15 18 3 20 Heap. Sort Slide 10/02/05

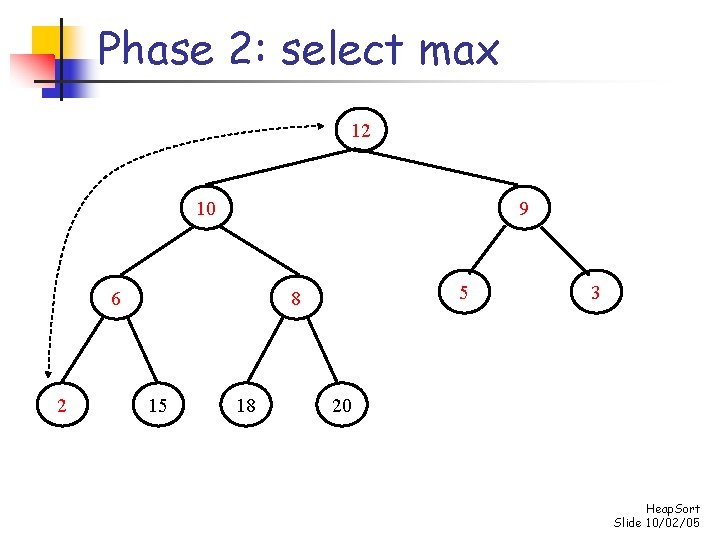
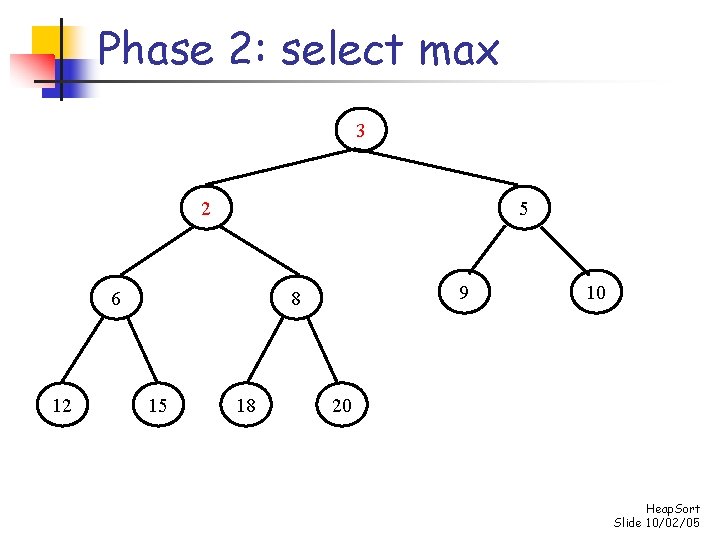
Phase 2: select max 2 10 9 6 12 5 8 15 18 3 20 Heap. Sort Slide 10/02/05

Phase 2: select max 10 8 9 6 12 5 2 15 18 3 20 Heap. Sort Slide 10/02/05

Phase 2: select max 3 8 9 6 12 5 2 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 9 8 5 6 12 3 2 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 3 8 5 6 12 9 2 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 8 6 5 3 12 9 2 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 2 6 5 3 12 9 8 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 6 3 5 2 12 9 8 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 2 3 5 6 12 9 8 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 5 3 2 6 12 9 8 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 2 3 5 6 12 9 8 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 3 2 5 6 12 9 8 15 18 10 20 Heap. Sort Slide 10/02/05

Phase 2: select max 2 3 5 6 12 9 8 15 18 10 20 Heap. Sort Slide 10/02/05

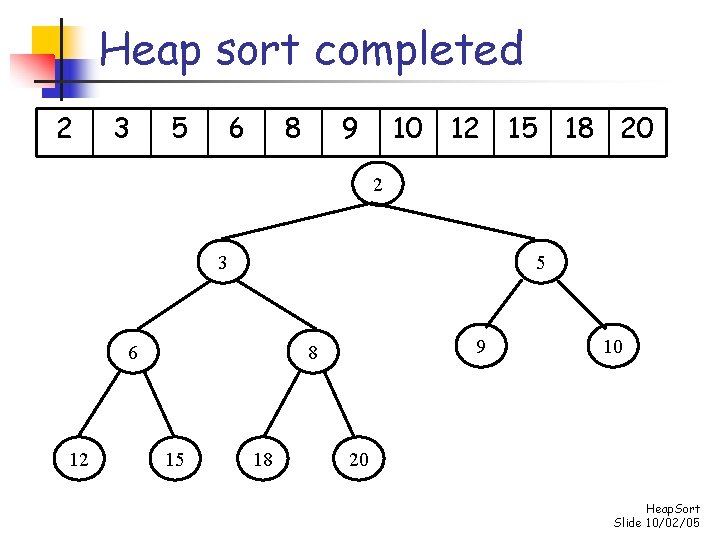
Heap sort completed 2 3 5 6 8 9 10 12 15 18 20 2 3 5 6 12 9 8 15 18 10 20 Heap. Sort Slide 10/02/05

Heap sort time complexity for i 1 to n-1 do insert element s[i] into the heap consisting of the elements s[0]…s[i-1] O( n log n ) O( log n ) operations for i n-1 down to 1 do swap s[0] and s[i] “demote” s[0] to its proper place in the heap consisting of the elements s[0]. . . s[i-1] O( n log n ) Heap. Sort Slide 10/02/05

About heap sort n Build heap phase can be improved to O( n ) if array is rearranged “bottom-up” n n n Overall complexity still O( n log n ) because of second phase O( n log n ) time complexity is guaranteed Note that heap sort is just a more clever version of selection sort since a maximum is repeatedly selected and placed in its proper position Heap. Sort Slide 10/02/05