He and hydrogenoid ions The one nucleuselectron system

He and hydrogenoid ions The one nucleus-electron system 1

topic • Mathematic required. • Schrödinger for a hydrogenoid • Orbital s • Orbital p 2

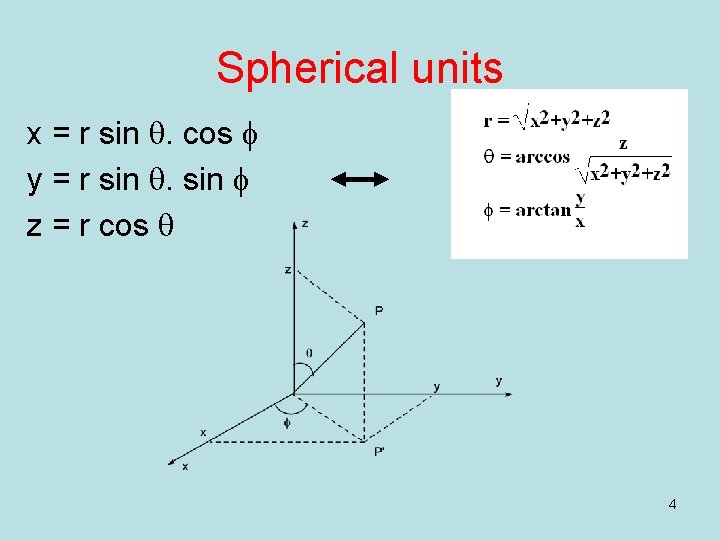
Two prerequisites Our world is 3 D! We need to calculate integrals and derivatives in full space (3 D). A system of one atom has spherical symmetry. Spherical units are appropriate. Y= Y(r, q, f) rather than Y= Y(x, y, z) except that D was defined in cartesian units. 3

Spherical units x = r sin q. cos f y = r sin q. sin f z = r cos q 4

derivation d. Y/dr for fixed q and f 5

derivation If we know making one derivation, we know how to make others, to make second derivatives, and the we know calculating the Laplacian, D 6

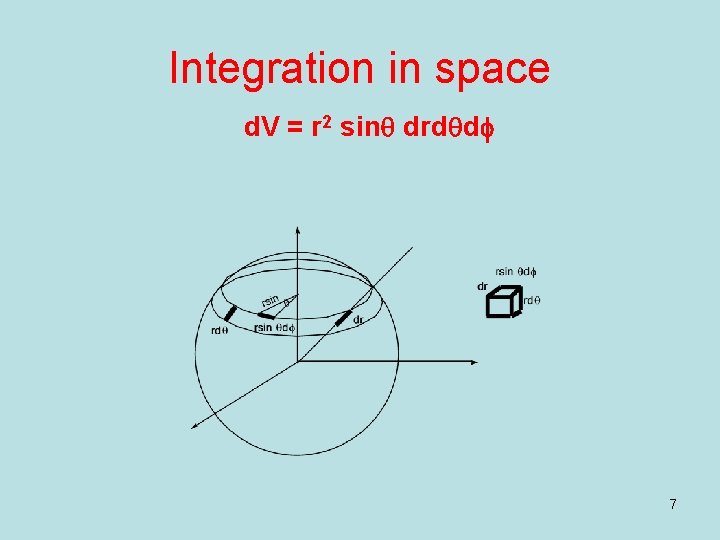
Integration in space d. V = r 2 sinq drdqdf 7

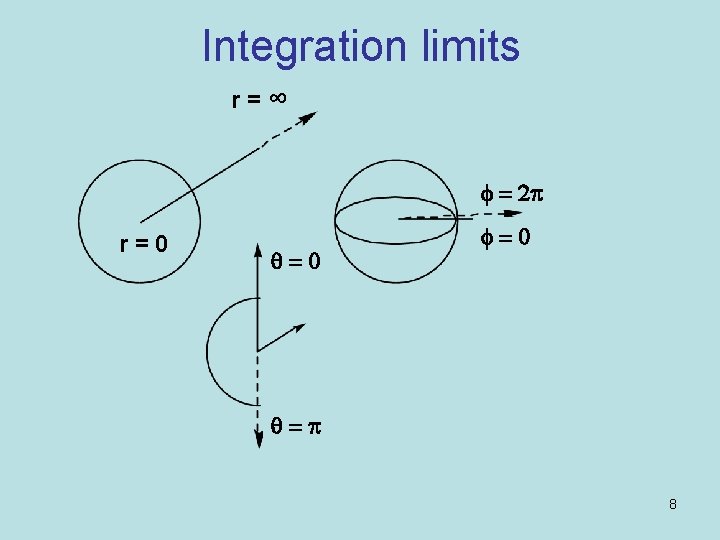
Integration limits r = ∞ f = 2 p r = 0 q=0 f=0 q=p 8

Integration in space 9

Integration in space Integration over q, f and r gives V = 4/3 pr 4 Volume of a sphere The integration over q and f gives the volume between two spheres of radii r and r+dr: d. V = 4 p r 2 dr Volume between two concentric spheres 10

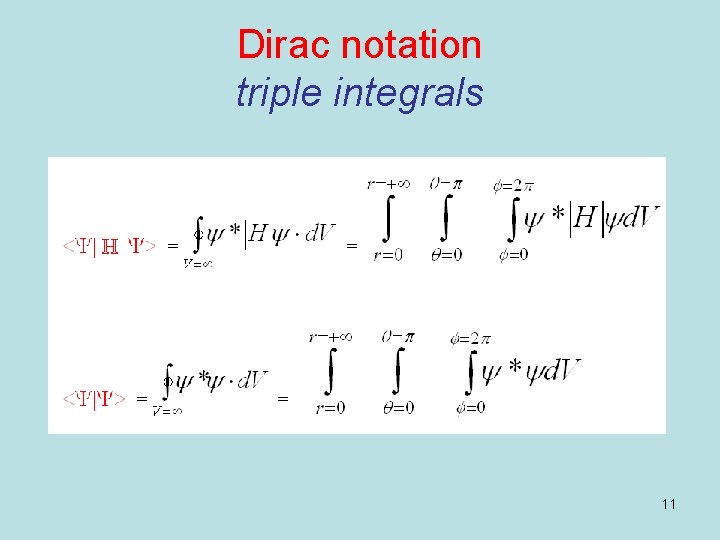
Dirac notation triple integrals 11

Spherical symmetry d. V = 4 p r 2 d. R 12

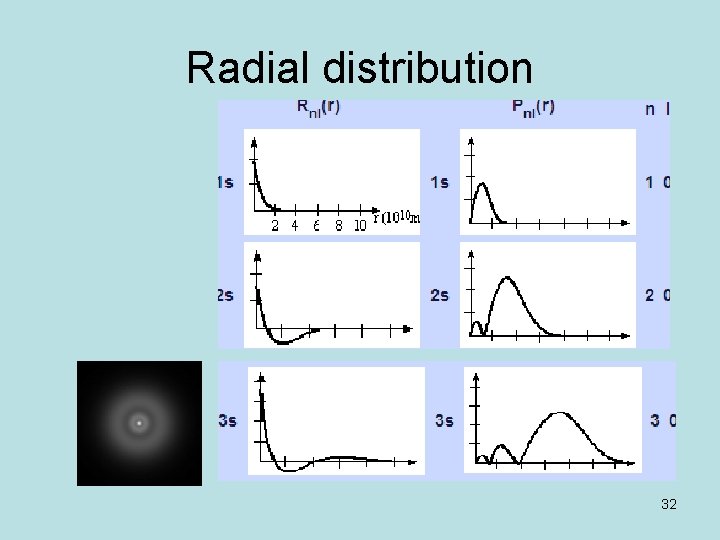
Radial density d. P/d. R = 4 p r 2 Y*Y It is the density of probability of finding a particule (an electron) at a given distance from a center (nucleus) It is not the density of probability per volume d. P/d. V= Y*Y It is defined relative to a volume that increases with r. The unit of Y is L-3/2 13

Schrödinger for a hydrogenoid (1 nucleus – 1 electron) The definition of an orbital atomic orbital: any function Ye(x, y, z) representing a stationary state of an atomic electron. Born-Oppenheimer approximation: decoupling the motion of N and e Y(x. N, y. N, z. N, xe, ye, ze)= Y(x. N, y. N, z. N)Y(xe, ye, ze) m. H=1846 me : When e- covers 1 m H covers 2. 4 cm, C 6. 7 mm and Au 1. 7 mm 14

Schrödinger for a hydrogenoid (1 nucleus – 1 electron) 15

Schrödinger for a hydrogenoid (1 nucleus – 1 electron) 16

Schrödinger for a hydrogenoid (1 nucleus – 1 electron) We first look for solutions valid for large r 17

Solution for large r Which of the 2 would you chose ? 18

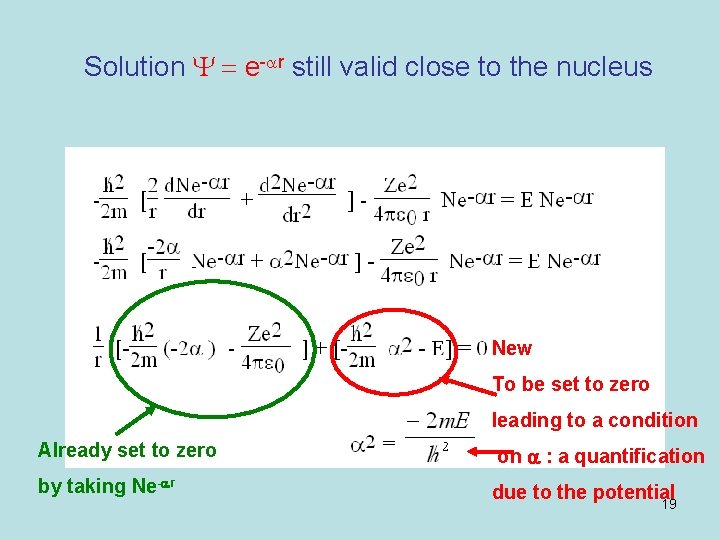
Solution Y = e-ar still valid close to the nucleus New To be set to zero leading to a condition Already set to zero on a : a quantification by taking Ne-ar due to the potential 19

The quantification of a is a quantification on E This energy is negative. The electron is stable referred to the free electron 20

Energy units 1 Rydberg = 21. 8 10 -19 Joules =14. 14 105 J mole-1 1 Rydberg = 13. 606 e. V = 0. 5 Hartree (atomic units) 1 e. V (charge for an electron under potential of 1 Volt) 1 e. V = 1. 602 10 -19 Joules = 96. 5 KJoules mole-1 (→ n = 8065. 5 cm-1) 1 e. V = = 24. 06 Kcal mole-1. 21

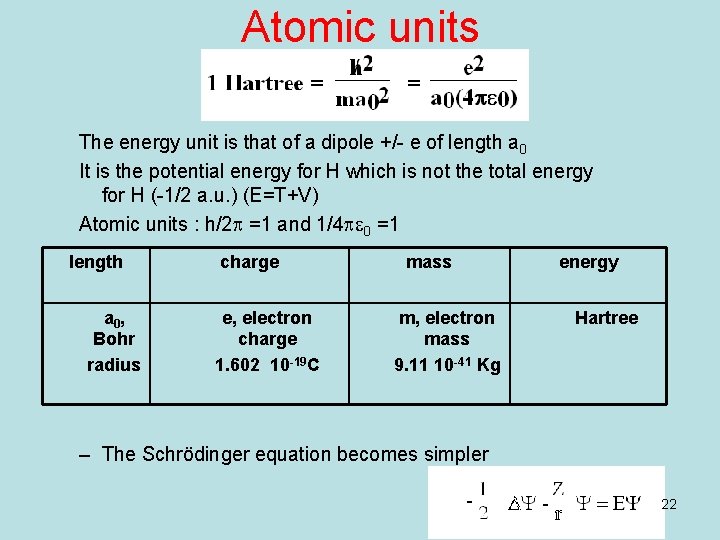
Atomic units The energy unit is that of a dipole +/- e of length a 0 It is the potential energy for H which is not the total energy for H (-1/2 a. u. ) (E=T+V) Atomic units : h/2 p =1 and 1/4 pe 0 =1 length a 0, Bohr radius charge e, electron charge 1. 602 10 -19 C mass m, electron mass 9. 11 10 -41 Kg energy Hartree – The Schrödinger equation becomes simpler 22

Normalization of Ne-ar From math textbooks The density of probability is maxima at the nucleus and decreases with the distance to the nucleus. 23

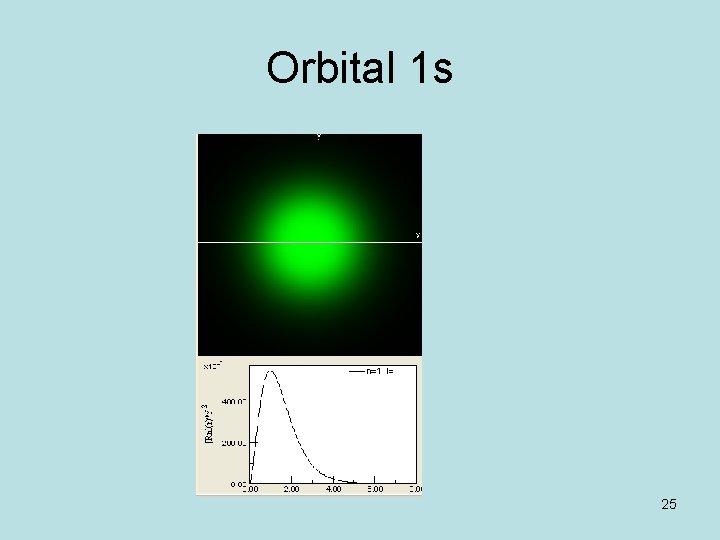
Radial density of probability a 0/Z is the most probable distance to the nucleus; it was found by Niels Bohr using a planetary model. The radial density close to zero refers to a dense volume but very small; far to zero, it corresponds to a large volume but an empty one 24

Orbital 1 s 25

Average distance to the nucleus Distance: Operator r larger than a 0/Z From math textbooks In an average value, the weight of heavy values dominates: (half+double)/2 = 1. 25 > 1) 26

Distances the nucleus 27

Excited states We have obtained a solution using Y = e-ar; it corresponds to the ground state. There are other quantified levels still lower than E=0 (classical domain where the e is no more attached to the nucleus)o We can search for other spherical function Y= Nn. Pn (r)e-ar where Pn(r) is a polynom of r of degree n-1 28

Orbital ns Principal quantum number E 2 s = Z 2 /4 E 1 s (H) Ens = Z 2 /n 2 E 1 s (H) Nodes: spheres for solution of equation Pn=O n-1 solutions Average distance 29

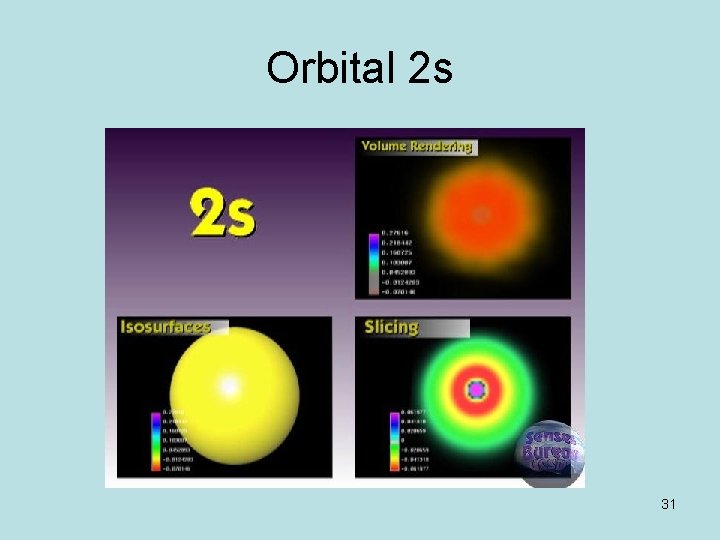
Orbital 2 s E 2 s = Z 2 /4 E 1 s (H) A more diffuse orbital: One nodal surface separating two regions with opposite phases: the = sphere for r=2 a 0/Z. Within this sphere the probability of finding the electron is only 5. 4%. The radial density of probability is maximum for r=0. 764 a 0/Z and r=5. 246 a 0/Z. Between 4. 426 et 7. 246 the probability of finding the electron is 64%. Average distance 5 a 0/Z 30

Orbital 2 s 31

Radial distribution 32

Resolution of Schrödinger equation in f, Solving the equation in q and f leads to define two other quantum numbers. They also can be defined using momentum instead of energy. For q: Angular Momentum (Secondary, Azimuthal) Quantum Number (l): l = 0, . . . , n-1. For f: Magnetic Quantum Number (ml): ml = -l, . . . , 0, . . . , +l. 33

Resolution of Schrödinger equation in f, the magnetic quantum number 34

Quantum numbers • Principal Quantum Number (n): n = 1, 2, 3, 4, …, ∞ Specifies the energy of an electron and the size of the orbital (the distance from the nucleus of the peak in a radial probability distribution plot). All orbitals that have the same value of n are said to be in the same shell (level). • Angular Momentum (Secondary, Azimunthal) Quantum Number (l): l = 0, . . . , n-1. • Magnetic Quantum Number (m): m = -l, . . . , 0, . . . , +l. Spin Quantum Number (ms): ms = +½ or -½. Specifies the orientation of the spin axis of an electron. An electron can spin in only one of two directions (sometimes called up and down). • 35

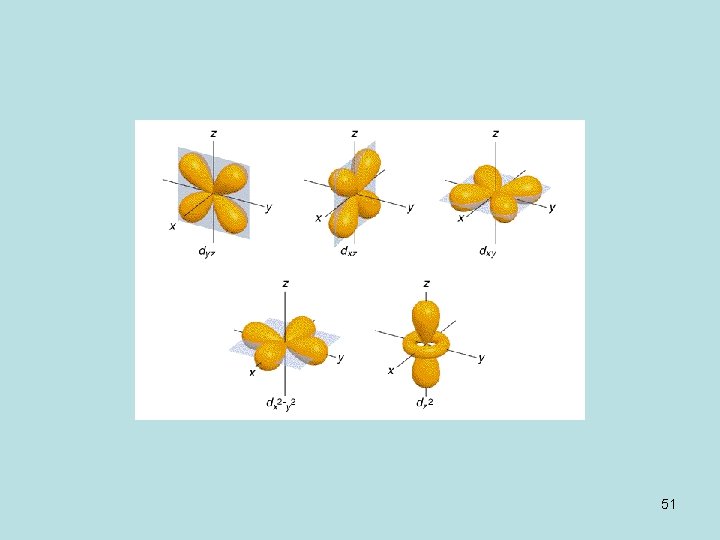
Name of orbitals The letter indicates the secondary Quantum number, l 1 s 2 s 2 p (2 p+1, 2 p 0, 2 p-1) The number indicates the Principal Quantum number 3 s 3 p (3 p+1, 3 p 0, 3 p-1) 3 d (3 p+2, 3 p+1, 3 p 0, 3 p-1 3 p-2 ) 4 s 4 p (4 p+1, 4 p 0, 4 p-1) The index indicates the magnetic 4 d (4 d+2, 4 d+1, 4 d 0, 4 d-1 4 d-2 ) Quantum number 4 f (4 f+3, 4 f+2, 4 f+1, 4 f 0, 4 f-1 4 f-2 , 4 f-3 36

Degenerate orbitals Depends only on the 2 2 E= Z /n (E 1 s. H) principal Quantum number 1 s 2 s 2 p (2 p+1, 2 p 0, 2 p-1) 3 s 3 p (3 p+1, 3 p 0, 3 p-1) 3 d (3 p+2, 3 p+1, 3 p 0, 3 p-1 3 p-2 ) 4 s 4 p (4 p+1, 4 p 0, 4 p-1) 4 d (4 d+2, 4 d+1, 4 d 0, 4 d-1 4 d-2 ) 4 f (4 f+3, 4 f+2, 4 f+1, 4 f 0, 4 f-1 4 f-2 , 4 f-3 1 function 4 functions 9 functions 16 functions Combination of degenerate functions: still OK for hydrogenoids. New expressions (same number); real expressions; hybridization. 37

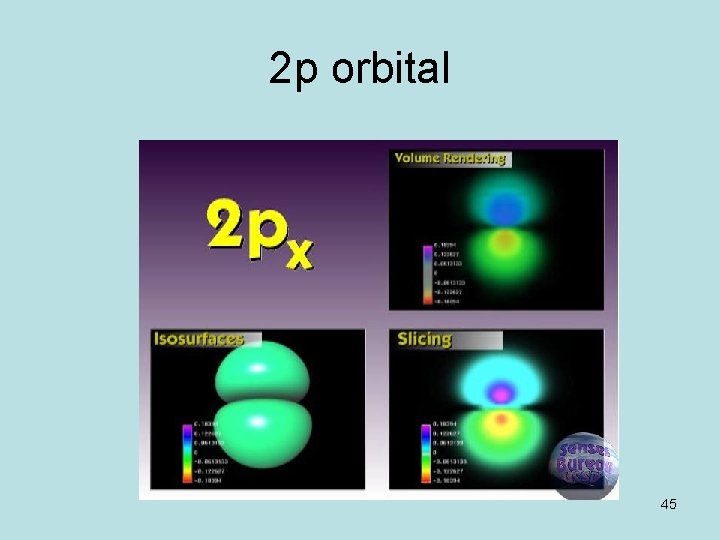
Functions 2 p 38

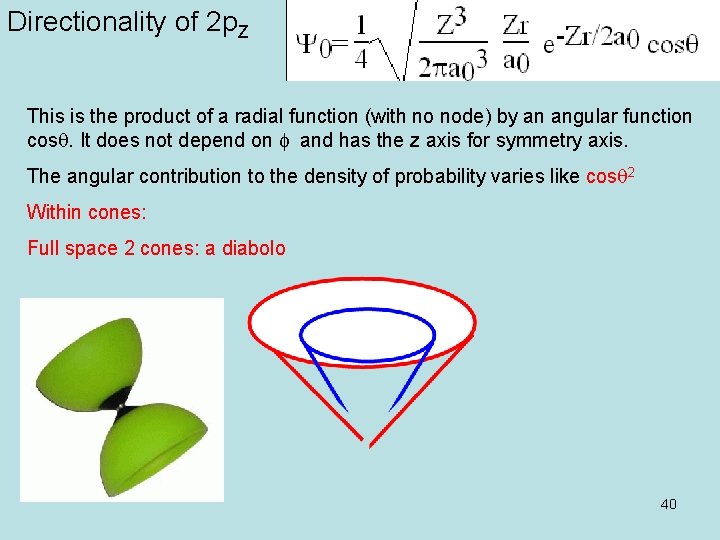
symmetry of 2 p. Z Nodes: No node for the radial part (except 0 and ∞) cosq = 0 corresponds to q=p/2 : the xy plane or z/r=0 : the xy plane The 2 pz orbital is antisymmetric relative to this plane cos(-q)=-cosq The z axis is a C∞ axis 39

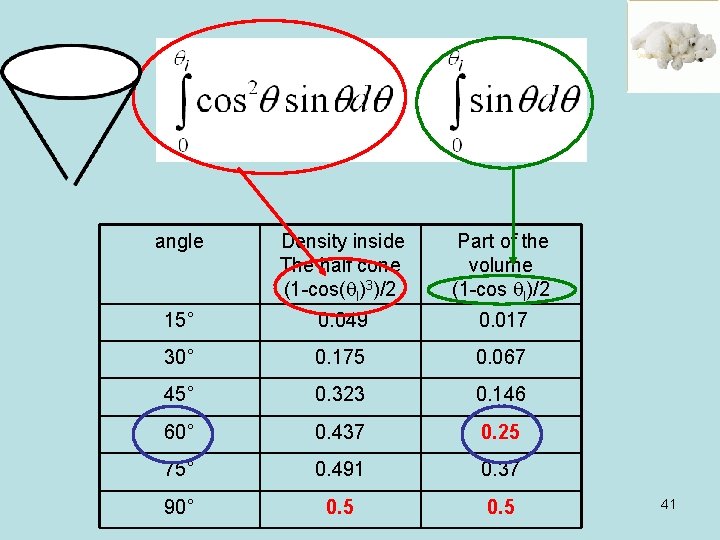
Directionality of 2 p. Z This is the product of a radial function (with no node) by an angular function cosq. It does not depend on f and has the z axis for symmetry axis. The angular contribution to the density of probability varies like cosq 2 Within cones: Full space 2 cones: a diabolo 40

angle Density inside The half cone (1 -cos(ql)3)/2 Part of the volume (1 -cos ql)/2 15° 0. 049 0. 017 30° 0. 175 0. 067 45° 0. 323 0. 146 60° 0. 437 0. 25 75° 0. 491 0. 37 90° 0. 5 41

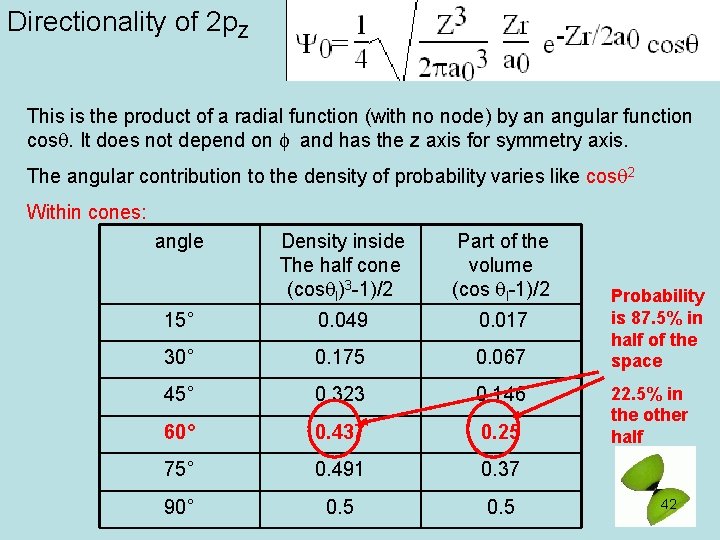
Directionality of 2 p. Z This is the product of a radial function (with no node) by an angular function cosq. It does not depend on f and has the z axis for symmetry axis. The angular contribution to the density of probability varies like cosq 2 Within cones: angle Density inside The half cone (cosql)3 -1)/2 Part of the volume (cos ql-1)/2 15° 0. 049 0. 017 30° 0. 175 0. 067 45° 0. 323 0. 146 60° 0. 437 0. 25 75° 0. 491 0. 37 90° 0. 5 Probability is 87. 5% in half of the space 22. 5% in the other half 42

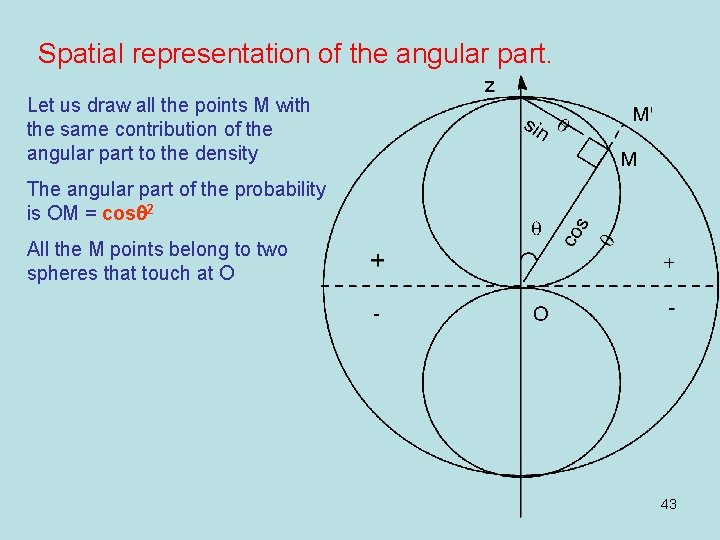
Spatial representation of the angular part. Let us draw all the points M with the same contribution of the angular part to the density The angular part of the probability is OM = cosq 2 All the M points belong to two spheres that touch at O 43

Isodensities, isolevels 44

2 p orbital 45

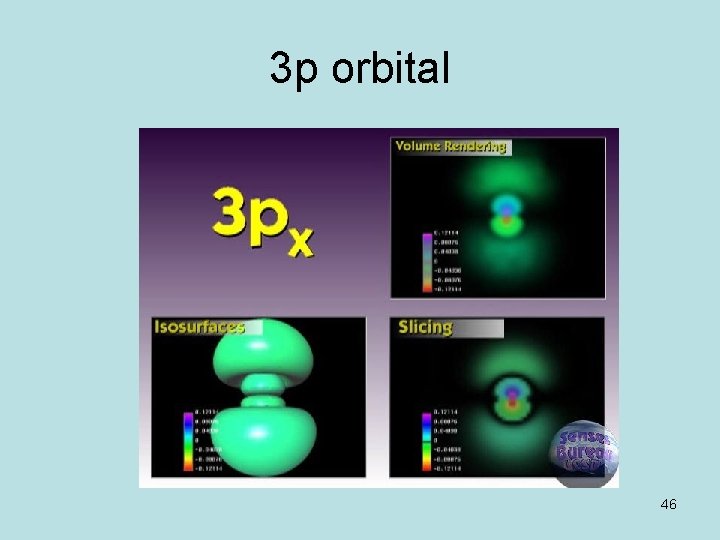
3 p orbital 46

The 2 px and 2 py orbitals are equivalent 47

One electron equally distributed on the three 2 p levels Y 2 is proportional to x 2/r 2+ y 2/r 2+ z 2/r 2=1 and thus does not depend on r: spherical symmetry An orbital p has a direction, like a vector. A linear combination of 3 p orbitals, is another p orbital with a different axis: The choice of the x, y, z orbital is arbitrary 48

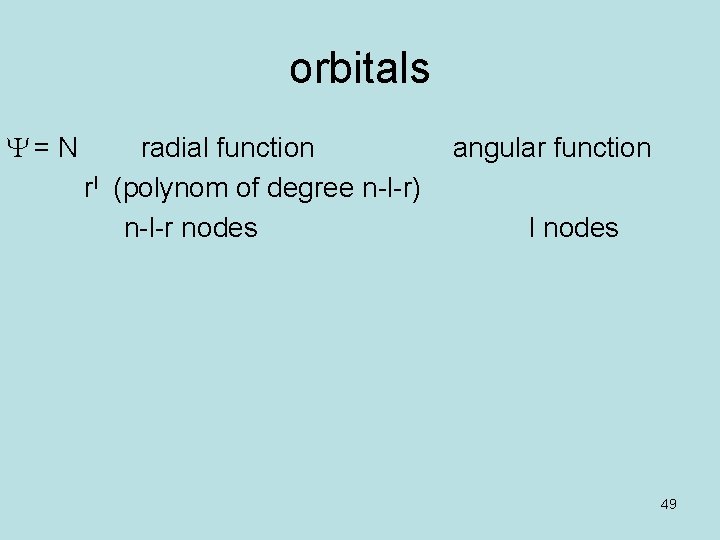
orbitals Y = N radial function angular function rl (polynom of degree n-l-r) n-l-r nodes l nodes 49

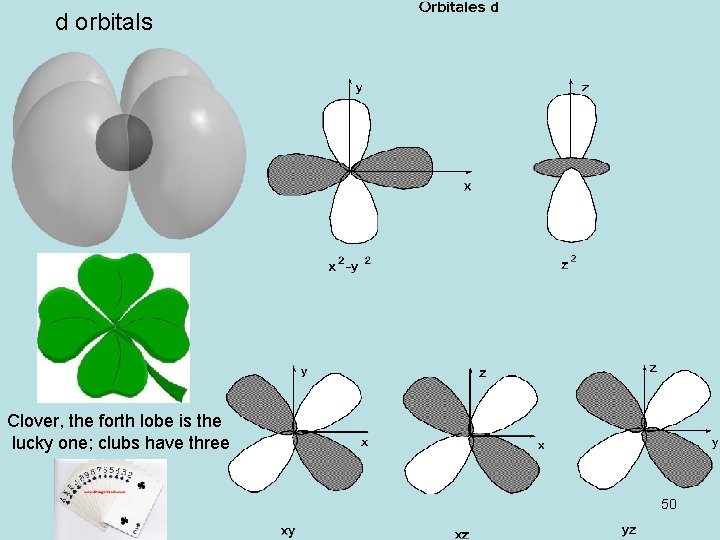
d orbitals Clover, the forth lobe is the lucky one; clubs have three 50

51

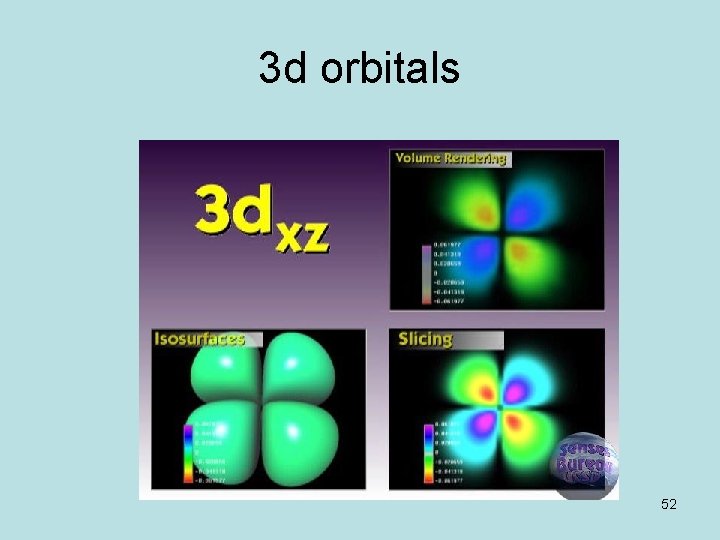
3 d orbitals 52

Compare the average radius of 1 s for the hydrogenoides whose nuclei are H and Pb. 207 Pb 82 Make comments on the 1 s orbital the atom Pb? 53

Name these orbitals Spherical coordinates x = r sin q cos f ; y = r sin q sin f ; z = r cos q 54

Paramagnetism Is an atom with an odd number of electron necessarily diamagnetic? Is an atom with an even number of electron necessarily paramagnetic? What is the (l, ml) values for Lithium? Is Li dia or para? Why? 55

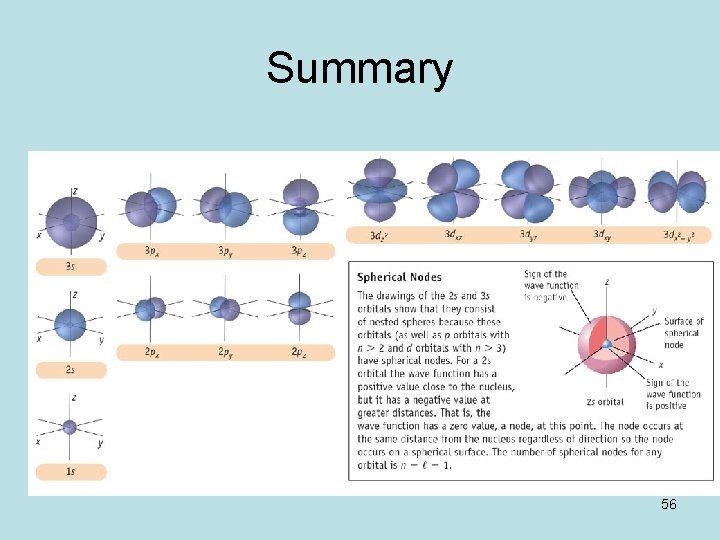
Summary 56

57