havo D deel 3 Samenvatting Hoofdstuk 10 Kenmerken

havo D deel 3 Samenvatting Hoofdstuk 10

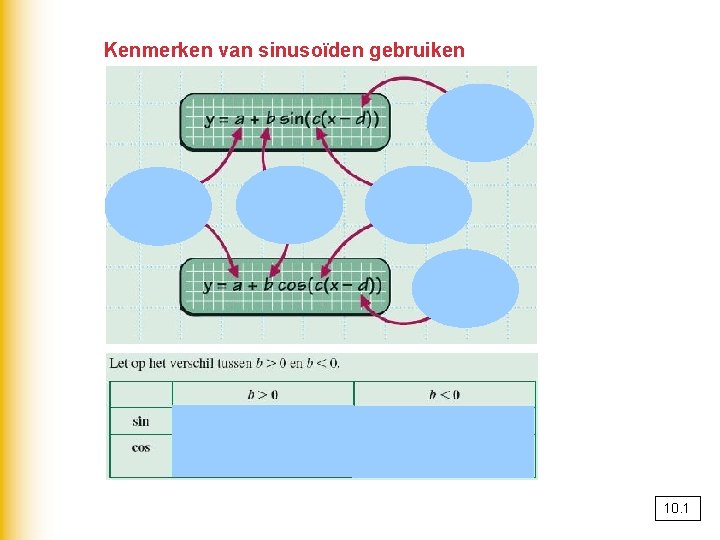
Kenmerken van sinusoïden gebruiken 10. 1

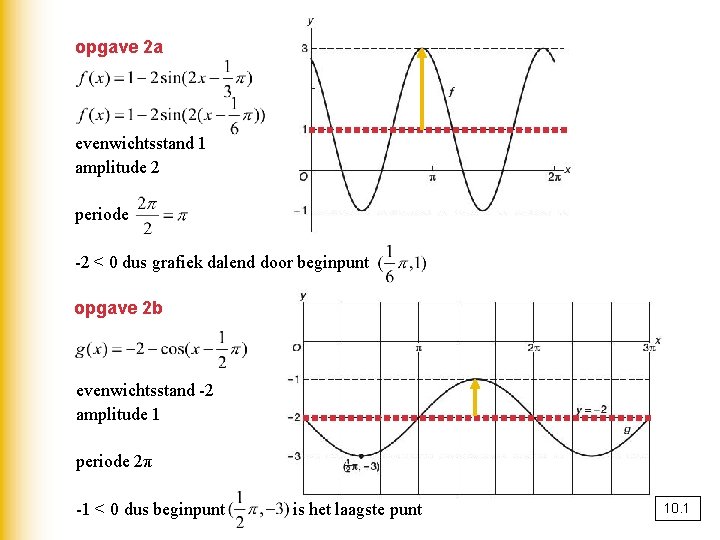
opgave 2 a evenwichtsstand 1 amplitude 2 periode -2 < 0 dus grafiek dalend door beginpunt opgave 2 b evenwichtsstand -2 amplitude 1 periode 2π -1 < 0 dus beginpunt is het laagste punt 10. 1

y De tangens-functie P(x. P, y. P) 1 O y. P α x. P Q ∟ Snijdt het tweede been van de draaiingshoek α de eenheidscirkel in P(x. P, y. P), x A (1, 0) dan is De grafiek van f(x) = tan(α) op het interval [0, 2π]. 10. 1

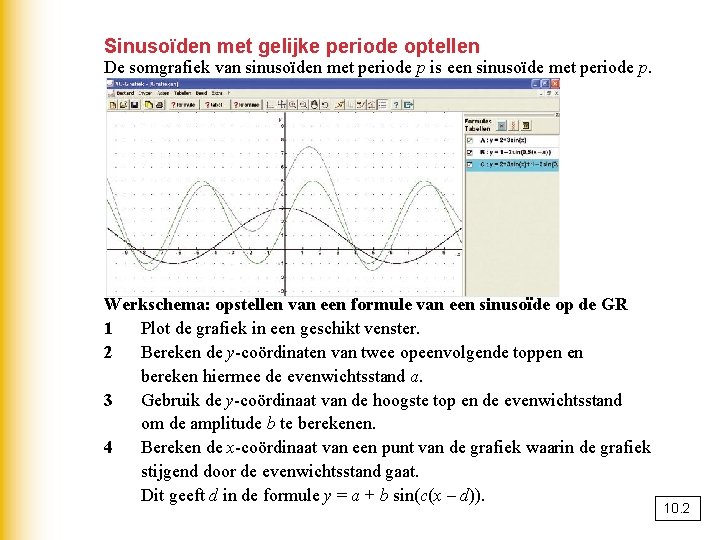
Sinusoïden met gelijke periode optellen De somgrafiek van sinusoïden met periode p is een sinusoïde met periode p. Werkschema: opstellen van een formule van een sinusoïde op de GR 1 Plot de grafiek in een geschikt venster. 2 Bereken de y-coördinaten van twee opeenvolgende toppen en bereken hiermee de evenwichtsstand a. 3 Gebruik de y-coördinaat van de hoogste top en de evenwichtsstand om de amplitude b te berekenen. 4 Bereken de x-coördinaat van een punt van de grafiek waarin de grafiek stijgend door de evenwichtsstand gaat. Dit geeft d in de formule y = a + b sin(c(x – d)). 10. 2

opgave 14 Voer in y 1 = 3 + sin(x), y 2 = sin(x – π) en y 3 = y 1 + y 2. Bij y 1 en y 2 is c = 1, dus ook bij y 3 is c = 1. Neem bijvoorbeeld Xmin = 0, Xmax = 2π, Ymin = 0 en Ymax = 6. De opties maximum en minimum bij y 3 geven de toppen (1, 833; 4, 932) en (4, 974; 1, 068). Dus a = =3 en b ≈ 4, 932 – 3 = 1, 932. Voer in y 4 = 3. Intersect met y 3 en y 4 geeft het snijpunt (0, 262; 3). d ≈ 0, 262 y = a + b sin(c(x – d)) y 3 = 3 + 1, 932 sin(x – 0, 262) 10. 2

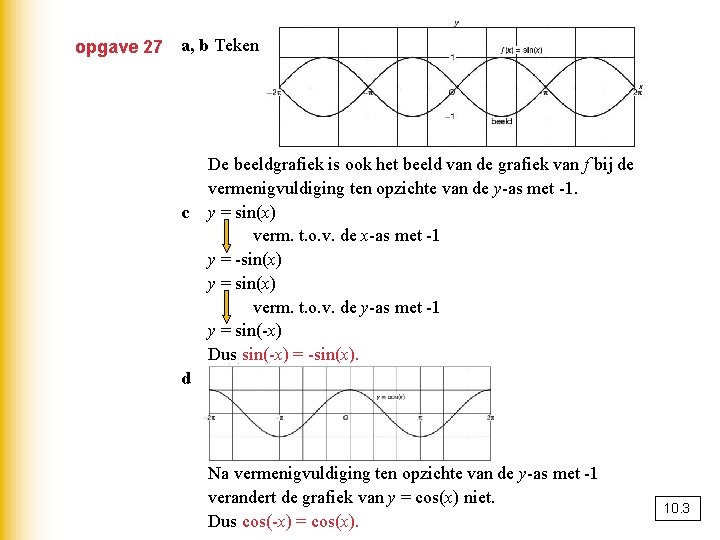
opgave 27 a, b Teken c De beeldgrafiek is ook het beeld van de grafiek van f bij de vermenigvuldiging ten opzichte van de y-as met -1. y = sin(x) verm. t. o. v. de x-as met -1 y = -sin(x) y = sin(x) verm. t. o. v. de y-as met -1 y = sin(-x) Dus sin(-x) = -sin(x). d Na vermenigvuldiging ten opzichte van de y-as met -1 verandert de grafiek van y = cos(x) niet. Dus cos(-x) = cos(x). 10. 3

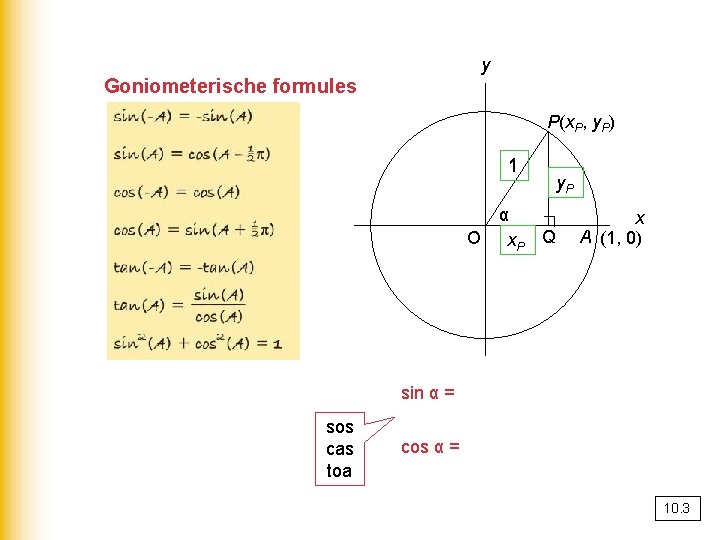
y Goniometerische formules P(x. P, y. P) 1 α x. P Q ∟ O sin α = sos cas toa cos α = PQ OP = OQ OP y. P = y. P 1 x A (1, 0) = y. P = x. P 10. 3

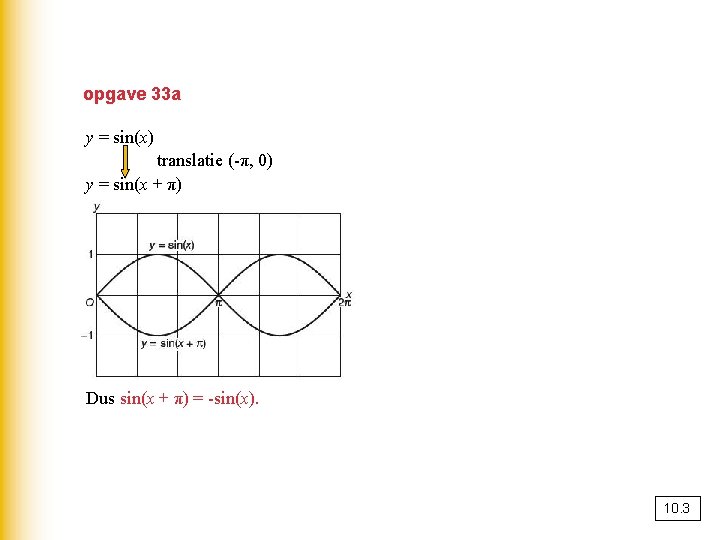
opgave 33 a y = sin(x) translatie (-π, 0) y = sin(x + π) Dus sin(x + π) = -sin(x). 10. 3

De afgeleide van y = sin(x) en y = cos(x) f (x) = sin(x) geeft f’ (x) = cos(x) geeft g’ (x) = -sin(x) voorbeeld f (x) = cos(2 x) Stel f (x) = cos(2 x) = cos(u) met u = 2 x f’ (x) = -sin(u) · 2 f’ (x) = -sin(2 x) · 2 = -2 sin(2 x) 10. 4

De quotiëntregel geeft 10. 4

opgave 44 u = 2 sin(30πt) geeft = 2 · cos(30πt) · 30π = 60π cos(30πt) = 60π · cos(30π · 0) = 60π cos(0) = 60π De snelheid op t = 0 is 60π cm/s. 10. 4