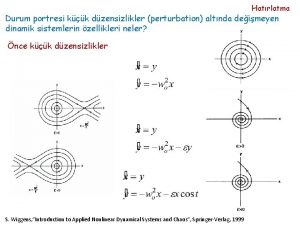
Hatrlatma Durum Denklemleri durum deikenleri kapasite gerilimleri endktans















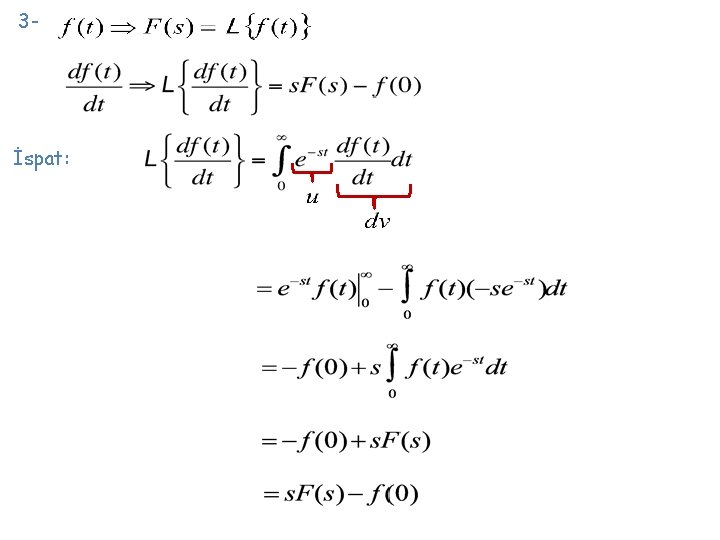
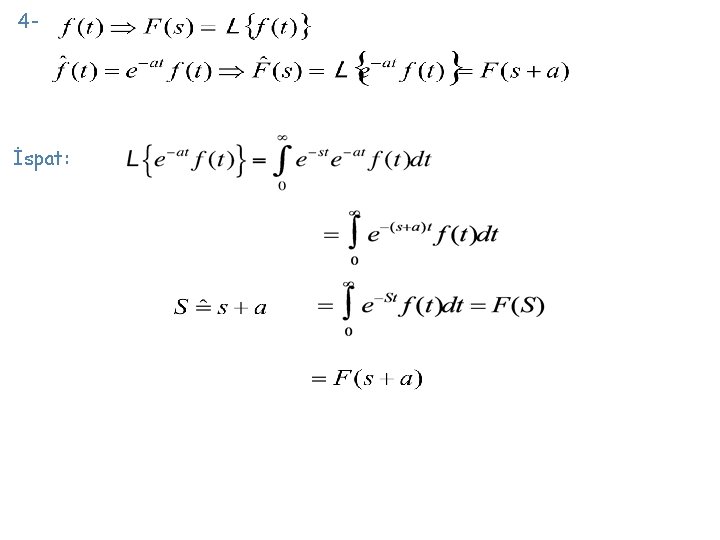
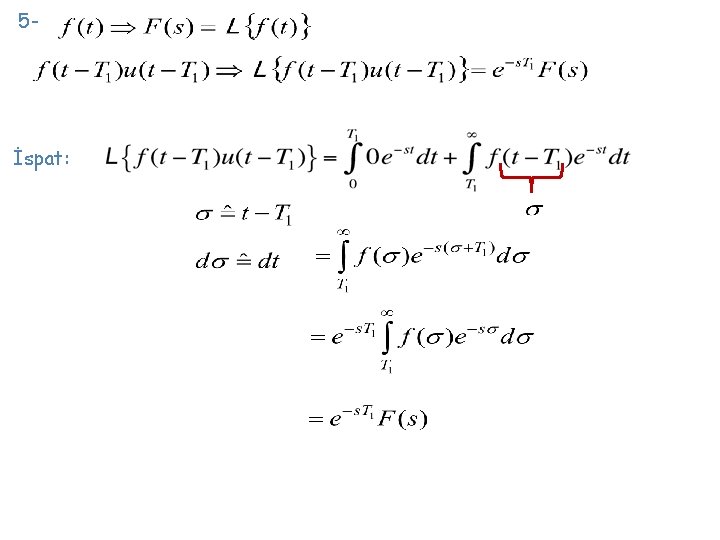
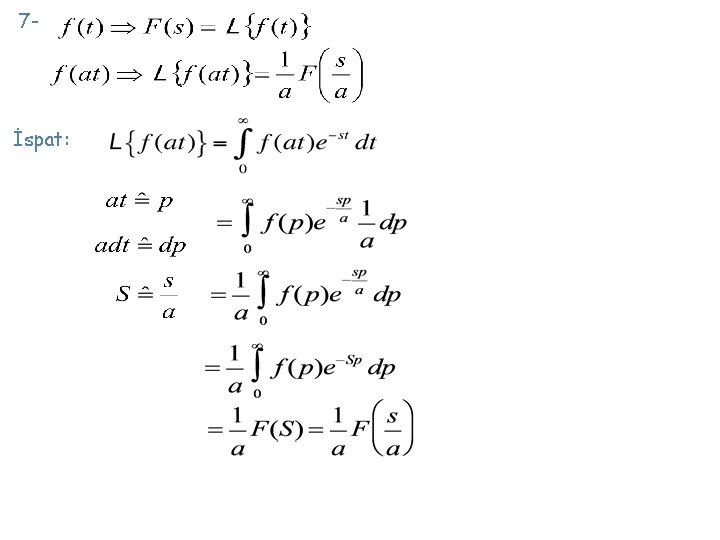

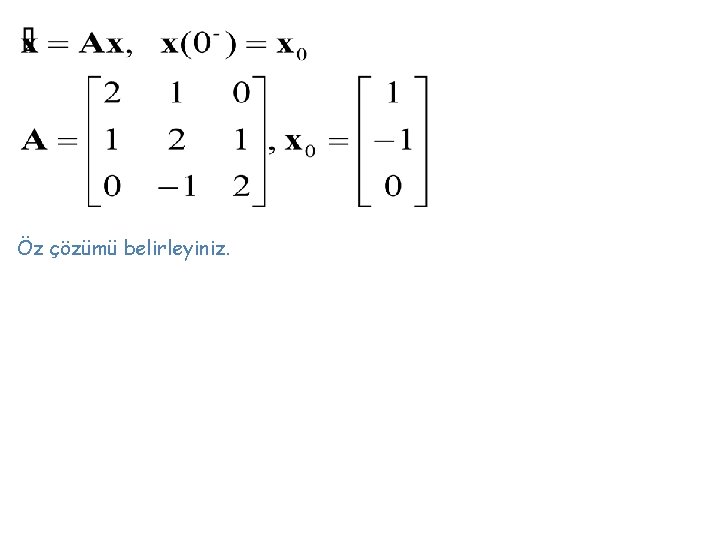



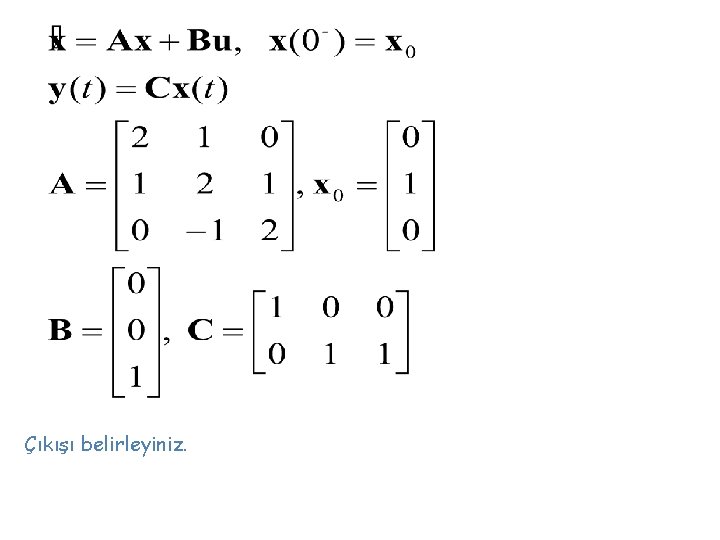
- Slides: 31

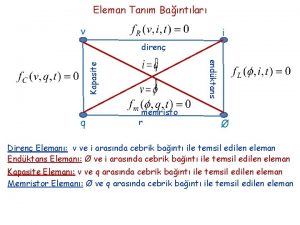
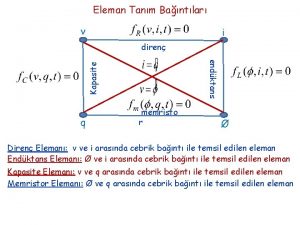
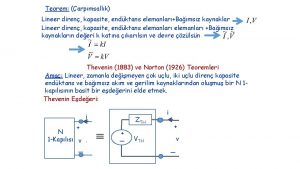
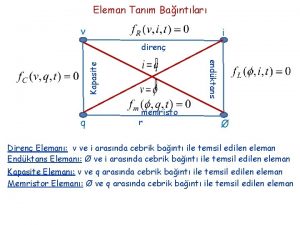
Hatırlatma: Durum Denklemleri durum değişkenleri - kapasite gerilimleri, endüktans akımları çıkış büyüklükleri - ilgilen eleman akımları ve gerilimleri giriş büyüklükleri - bağımsız akım kaynaklarının akımları ve bağımsız gerilim kaynaklarının gerilimleri EDT dersinde n=2 için çözümler bulundu:

2. Mertebeden Diferansiyel Denklemlerin Çözümü Homojen kısım: Çözüm Tahmini belirlememiz gereken kaç büyüklük var? sıfırdan farklı çözümlerin olması nasıl mümkün olur? Karakteristik Denklem

Karakteristik denklemin kökleri: Belirlememiz gereken özvektör özdeğerler Hangi uzayın elemanı? ‘e ilişkin özvektör ‘ye ilişkin özvektör Özel çözüm: Temel Matris Nasıl belirleyeceğiz? Tam çözüm:

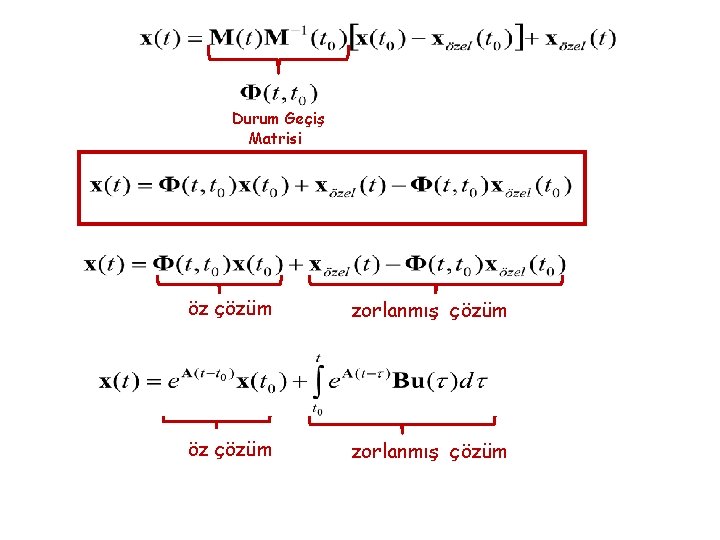
Durum Geçiş Matrisi öz çözüm zorlanmış çözüm

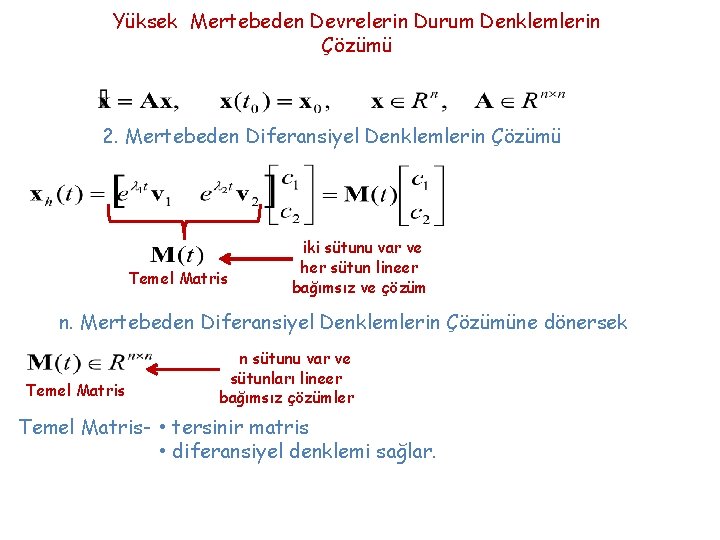
Yüksek Mertebeden Devrelerin Durum Denklemlerin Çözümü 2. Mertebeden Diferansiyel Denklemlerin Çözümü Temel Matris iki sütunu var ve her sütun lineer bağımsız ve çözüm n. Mertebeden Diferansiyel Denklemlerin Çözümüne dönersek Temel Matris n sütunu var ve sütunları lineer bağımsız çözümler Temel Matris- • tersinir matris • diferansiyel denklemi sağlar.

Durum Geçiş Matrisi: Durum Geçiş Matrisi, matris diferansiyel denklemini çözer:

İlgilendiğimiz Sistemler Durum Geçiş matrisi Durum geçiş matrisinin özellikleri 1 -

2 - İlgilendiğimiz Sistemler Çözüm

İlgilendiğimiz Sistemler Varsayım: * Varsayımı yerleştirirsek * ve **’dan **

Lineer Zamanla Değişmeyen Sistemler için: Çözümü bulmak için ‘nin belirlenmesi gerekiyor.

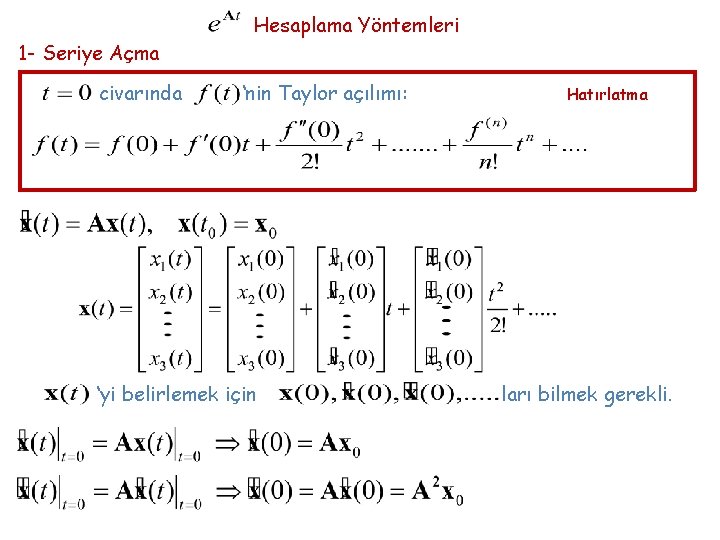
Hesaplama Yöntemleri 1 - Seriye Açma civarında ‘nin Taylor açılımı: ‘yi belirlemek için Hatırlatma ları bilmek gerekli.


2 - Jordan Kanonik Yapısı Benzerlik dönüşümü ile matris özel bir yapıya getirilecek Cebrik katlılığı olan bir Jordan bloğu bulunur. özdeğeri için tane ve buna geometrik katlılık denir. Bu sayı kullanılarak bulunabilen lineer bağımsız özvektör sayısına eşittir. Diğer (genelleştirilmiş) özvektörler bulunan her bir özvektör için iterasyonu yardımıyla bulunabilir.

P nin sütunları. . . . . den oluşur. Buradan nasıl elde edilir ?

Jordan kanonik form ile ‘yi hesaplayınız!

>> A=[0 0 0 1; 2 1 -1 -1 0 -1; 0 0 2 1 0 0; 0 0 0 2 0 0; 0 0 2 0; -1 0 0 2 ] A = 0 0 0 1 2 1 -1 0 0 2 1 0 0 0 0 0 2 0 -1 0 0 2 >> [P, J]=jordan(A) P = 0 0 0 2 -1 0 2 -3 -2 0 1 0 0 0 0 1 0 0 0 2 1 0 J = 2 1 0 0 0 2 0 0 0 1 1 0 0 0 0 0 1 0 0 0 2 >> expm(J*t) ans = [ exp(2*t), t*exp(2*t), 0, 0, 0] [ 0, 0, exp(t), t*exp(t), (t^2*exp(t))/2, 0] [ 0, 0, exp(t), t*exp(t), 0] [ 0, 0, 0, 0, exp(2*t )] >> pretty(ans)

3 - Laplace Dönüşümü Ön bilgi: Laplace dönüşümü Tanım: için sürekli ya da parça sürekli bir fonksiyon olsun, koşulunu sağlıyorsa ‘nin Laplace dönüşümü aşağıdaki bağıntı ile tanımlanır: ile Pierre-Simon, marquis de Laplace 1749 -1827 ‘nin Laplace dönüşümünü ile ters Laplace dönüşümünü belirteceğiz.

Laplace dönüşümünün özellikleri 1 - Teklik İspatı derin matematik gerektiriyor. 2 - Lineerlik ve İspat: sabit büyüklük olmak üzere
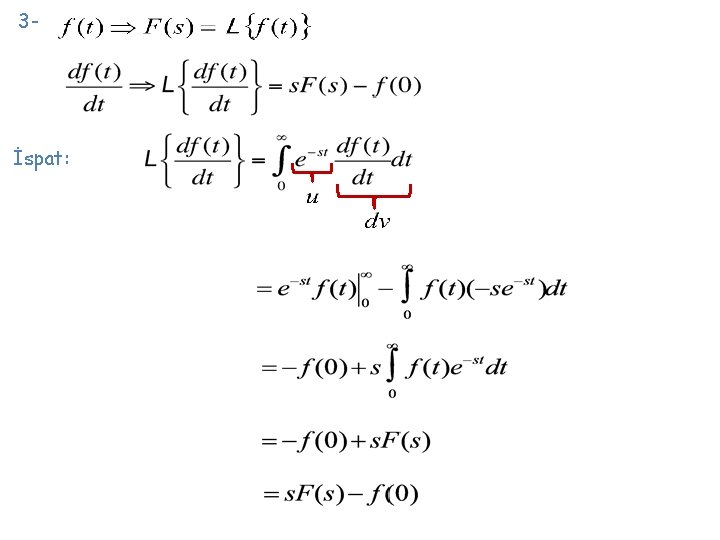
3 - İspat:
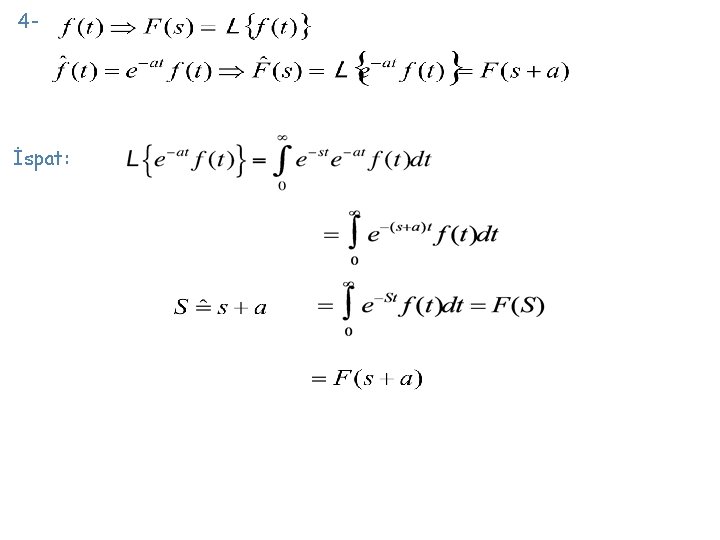
4 - İspat:
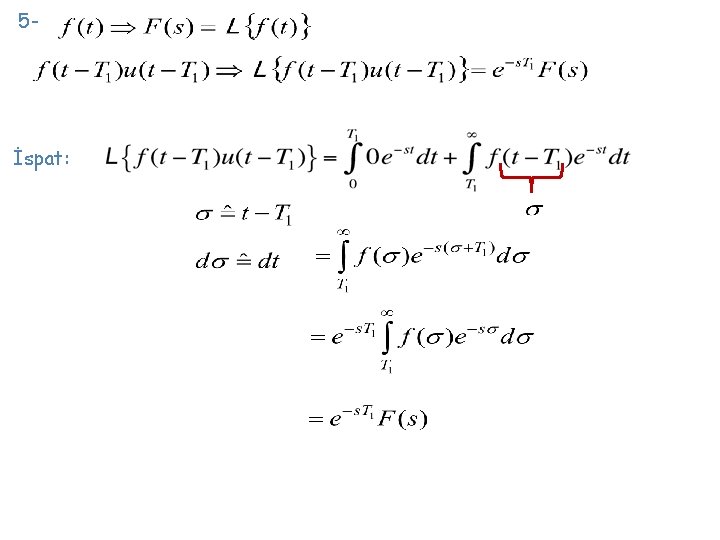
5 - İspat:

6 - İspat:
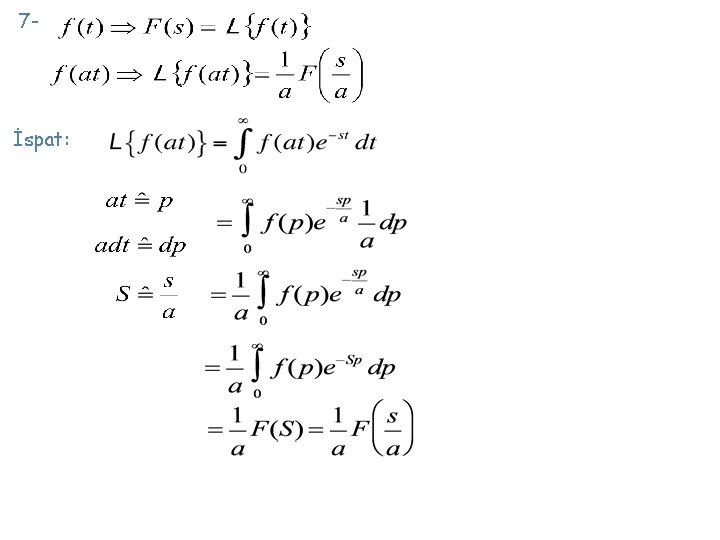
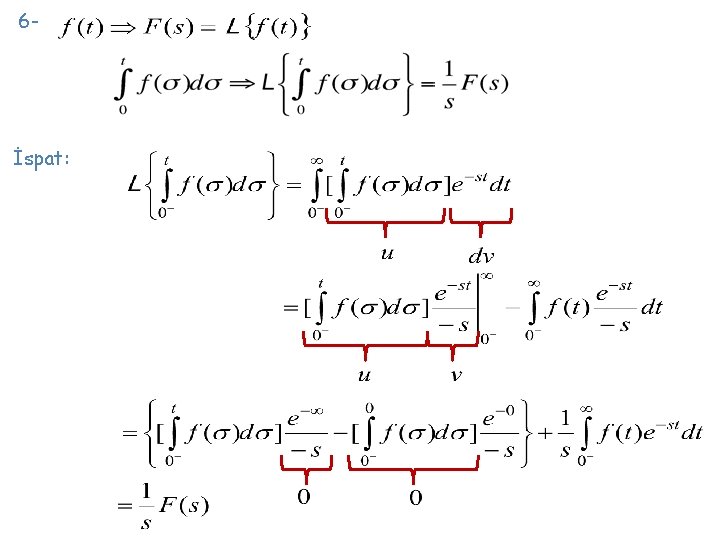
7 - İspat:

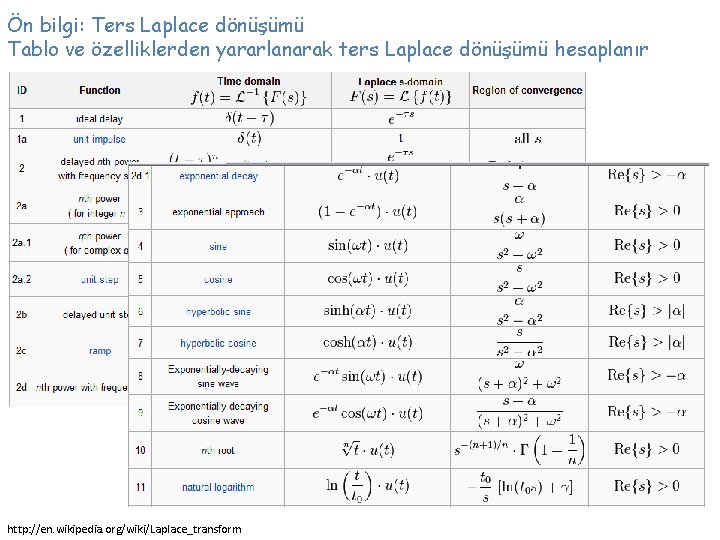
Ön bilgi: Ters Laplace dönüşümü Tablo ve özelliklerden yararlanarak ters Laplace dönüşümü hesaplanır http: //en. wikipedia. org/wiki/Laplace_transform

Laplace Dönüşümünden Faydalanarak Öz Çözümün Bulunması öz çözüm
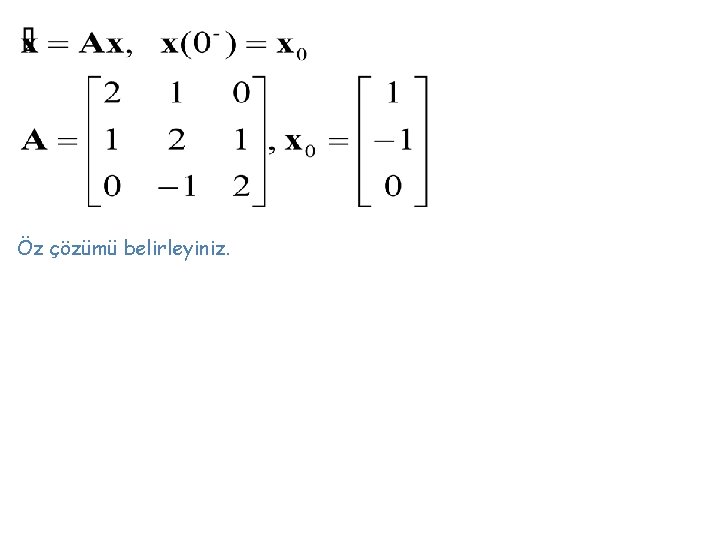
Öz çözümü belirleyiniz.

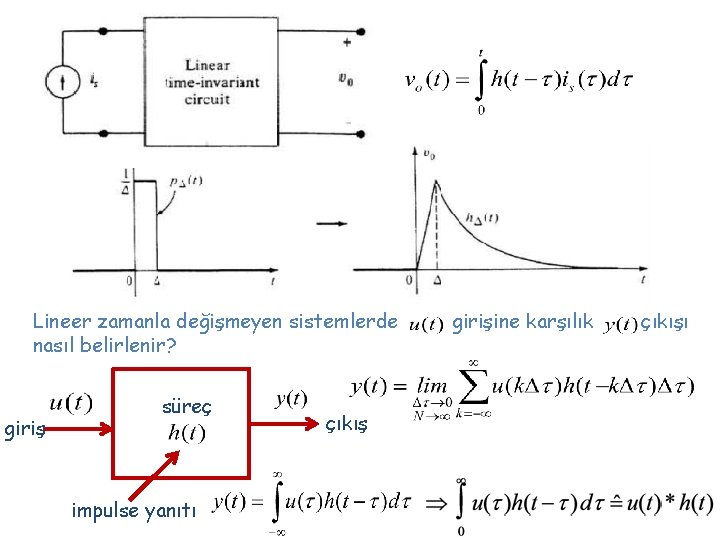
Lineer zamanla değişmeyen sistemlerde nasıl belirlenir? giriş süreç impulse yanıtı çıkış girişine karşılık çıkışı


Laplace Dönüşümünden Faydalanarak Zorlanmış Çözümün Bulunması 0 zorlanmış çözüm

Laplace Dönüşümünden Faydalanarak Tam Çözümün Bulunması Çıkışın Belirlenmesi
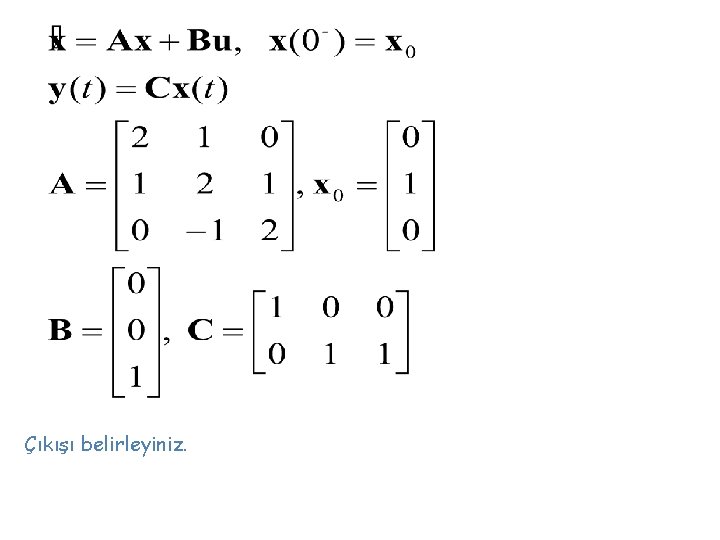
Çıkışı belirleyiniz.
 Durum denklemleri
Durum denklemleri Durum geçiş matrisi
Durum geçiş matrisi Kapasite seçimini etkileyen faktörler
Kapasite seçimini etkileyen faktörler Fdtd nedir
Fdtd nedir Birleşik eylem nedir
Birleşik eylem nedir Durum bildiren fiil
Durum bildiren fiil Doğrulayıcı ve yanlışlayıcı durum örneklemesi
Doğrulayıcı ve yanlışlayıcı durum örneklemesi Sik dürüm
Sik dürüm Maya devita lokanata
Maya devita lokanata žíhané vývody
žíhané vývody Dramatik durum nedir
Dramatik durum nedir Durum geçiş matrisi hesaplama
Durum geçiş matrisi hesaplama Afat acil butonu
Afat acil butonu Tabakalı örnekleme
Tabakalı örnekleme Vasıta eki nedir
Vasıta eki nedir Pekiştirilmiş zarf örnekleri
Pekiştirilmiş zarf örnekleri 5 temel duygu
5 temel duygu Finansal durum tablosu
Finansal durum tablosu Den hali
Den hali Olay hikayesinin en önemli temsilcisi
Olay hikayesinin en önemli temsilcisi Performans güçleri analizi nedir
Performans güçleri analizi nedir Durum geçiş matrisi hesaplama
Durum geçiş matrisi hesaplama Tek hekim raporu nedir
Tek hekim raporu nedir Dürüm 06
Dürüm 06 Ad durum eki
Ad durum eki Yer yön zarfı
Yer yön zarfı Durum geçiş matrisi
Durum geçiş matrisi Durum uzayı
Durum uzayı Tomsuklu osb son durum
Tomsuklu osb son durum Apex linguae epitel
Apex linguae epitel Acil durum telefon numaraları
Acil durum telefon numaraları Durum yönünden belirtmek ne demek
Durum yönünden belirtmek ne demek