Hashing Techniques 11 Overview Hash string key integer

Hashing Techniques 11

Overview • Hash[ “string key”] ==> integer value • Hash Table Data Structure : Use-case – To support insertion, deletion and search in average-case constant time • Assumption: Order of elements irrelevant • ==> data structure not useful for sorting • Hash table ADT – Implementations – Analysis – Applications 2 2

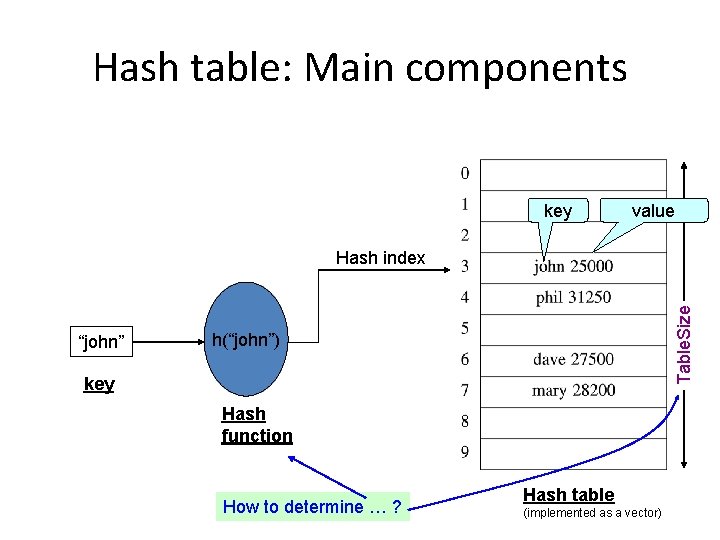
Hash table: Main components key value “john” Table. Size Hash index h(“john”) key Hash function How to determine … ? Hash table (implemented as a vector)

Hash Table • Insert Hash key Hash function – T [h(“john”)] = T[3] = <“john”, 25000> • Delete – T [h(“john”)] = NULL Data record • Search – Return T [h(“john”)] • What if h(“john”) = h(“joe”) ? – “collision” 5

Factors affecting Hash Table Design • Hash function • Table size – Usually fixed at the start • Collision handling scheme

h(“key”) ==> hash table index Hash Function Properties • A hash function maps key to integer – Constraint: Integer should be between [0, Table. Size-1] • A hash function can be a many-to-one mapping (causing collision) • Collision occurs when hash function maps two or more keys to same array index • Collisions cannot be avoided but its chances can be reduced using a good hash function 7

h(“key”) ==> hash table index Hash Function Properties • A good hash function should have the properties: – Different keys should ideally map to different indices – Hash function should ideally distribute keys uniformly over table – Minimize chance of collisions 8

Hash Function - Effective use of table size • Simple hash function (assume integer keys) – h(Key) = Key mod Table. Size • For random keys, h() distributes keys evenly over table • What if Table. Size = 100 and keys are multiples of 10? • Better if Table. Size is a prime number – Not too close to powers of 2 or 10

Hash Function for String Keys A very simple function to map strings to integers: • Add up character ASCII values (0 -127) to produce integer keys • E. g. , “abcd” = 97+98+99+100 = 394 • ==> h(“abcd”) = 394 % Table. Size • Small strings may not use all of table • Strlen(S) * 127 < Table. Size • Anagrams will map to the same index • h(“abcd”) == h(“dbac”)

Hash Function for String Keys • Approach 2 – Treat first 3 characters of string as base-27 integer (26 letters plus space) – Key = S[0] + (27 * S[1]) + (272 * S[2]) – Assumes first 3 characters randomly distributed • Not true of English Apple Apply Appointment Apricot collision 11

Hash Function for String Keys • Approach 3 – Use all N characters of string as an Ndigit base-K integer – Choose K to be prime number larger than number of different digits (characters) • I. e. , K = 29, 31, 37 – If L = length of string S, then – Use Horner’s rule to compute h(S) – Limit L for long strings Problem: A very long string can evaluate to a very large number 12

Resolving Collisions • What happens when h(k 1) = h(k 2)? – ==> collision ! • Collision resolution strategies – Separate Chaining (Open hashing) • Store colliding keys in a linked list at the same hash table index – Open addressing (Closed hashing) • Store colliding keys elsewhere in the table 13

Separate Chaining Collision resolution approach #1

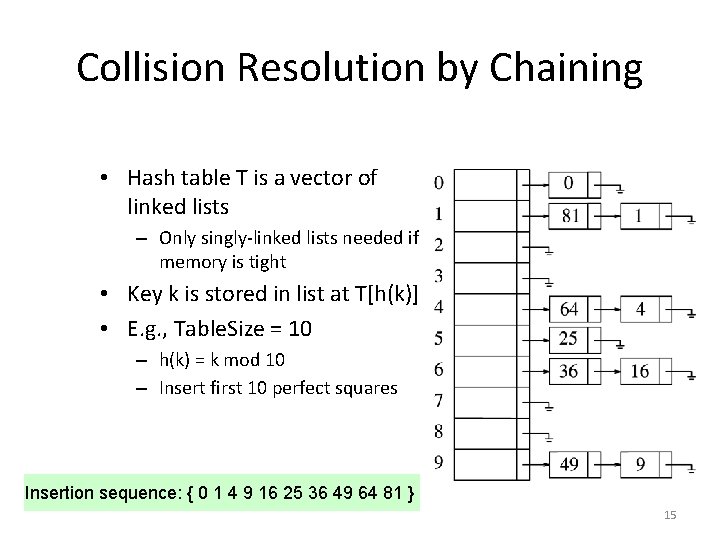
Collision Resolution by Chaining • Hash table T is a vector of linked lists – Only singly-linked lists needed if memory is tight • Key k is stored in list at T[h(k)] • E. g. , Table. Size = 10 – h(k) = k mod 10 – Insert first 10 perfect squares Insertion sequence: { 0 1 4 9 16 25 36 49 64 81 } 15

Collision Resolution by Chaining: Analysis • Load factor λ of a hash table T – – N = number of elements in T M = size of T λ = N/M I. e. , λ is the average length of a chain • Unsuccessful search O(λ) – Same for insert • Successful search O(λ/2) • Ideally, want λ ≤ 1 (not a function of N)

Open Addressing Collision resolution approach #2

Collision Resolution by Open Addressing When a collision occurs, look elsewhere in the table for an empty slot • Advantages over chaining – No need for list structures – No need to allocate/deallocate memory during insertion/deletion (slow) • Disadvantages – Slower insertion – May need several attempts to find an empty slot – Table needs to be bigger (than chaining-based table) to achieve average-case constant-time performance • Load factor λ ≈ 0. 5 18

Collision Resolution by Open Addressing • Probe sequence – – Sequence of slots in hash table to search h 0(x), h 1(x), h 2(x), … Needs to visit each slot exactly once Needs to be repeatable (so we can find/delete what we’ve inserted) • Hash function – hi(x) = (h(x) + f(i)) mod Table. Size – f(0) = 0 ==> first try 19

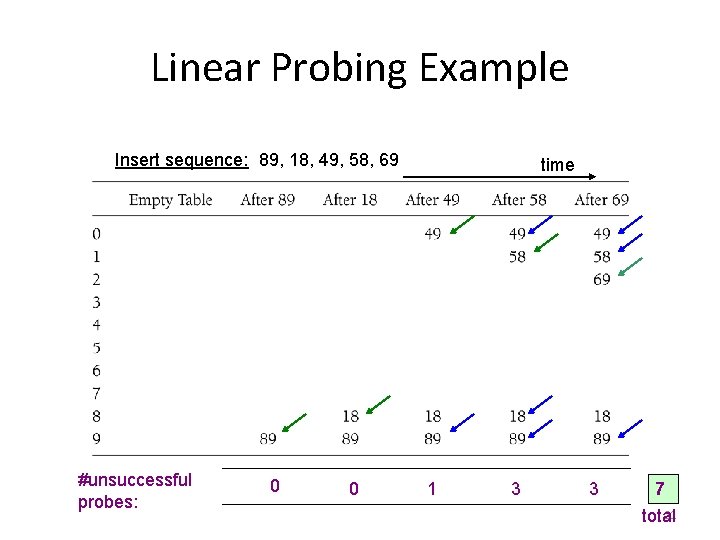
ith probe index = first probe index Linear Probing +i • f(i) = is a linear function of i, e. g. , f(i) = i – hi(x) = (h(x) + i) mod Table. Size – Probe sequence: +0, +1, +2, +3, +4, … • Example: h(x) = x mod Table. Size – – h 0(89) = (h(89)+f(0)) mod 10 = 9 h 0(18) = (h(18)+f(0)) mod 10 = 8 h 0(49) = (h(49)+f(0)) mod 10 = 9 (X) h 1(49) = (h(49)+f(1)) mod 10 = (h(49)+ 1 ) mod 10 = 0

Linear Probing Example Insert sequence: 89, 18, 49, 58, 69 #unsuccessful probes: 0 0 time 1 3 3 7 21 total

Linear Probing: Issues • Probe sequences can get long • Primary clustering – Keys tend to cluster in one part of table – Keys that hash into cluster will be added to the end of the cluster (making it even bigger) 22

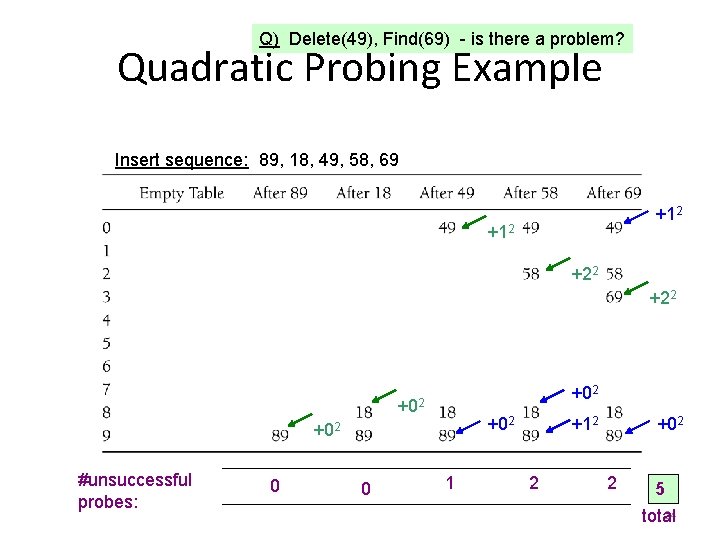
Quadratic Probing • Avoids primary clustering • f(i) is quadratic in I, e. g. , f(i) = i 2 – hi(x) = (h(x) + i 2) mod Table. Size – Probe sequence: +0, +1, +4, +9, +16, … • Example: – h 0(58) = (h(58)+f(0)) mod 10 = 8 (X) – h 1(58) = (h(58)+f(1)) mod 10 = 9 (X) – h 2(58) = (h(58)+f(2)) mod 10 = 2 23

Q) Delete(49), Find(69) - is there a problem? Quadratic Probing Example Insert sequence: 89, 18, 49, 58, 69 +12 +22 +02 #unsuccessful probes: 0 0 +12 +02 1 2 +02 2 5 24 total

Quadratic Probing • May cause “secondary clustering” • Deletion – Emptying slots can break probe sequence and could cause find stop prematurely – Lazy deletion • Differentiate between empty and deleted slot • Skip deleted slots • Slows operations (effectively increases λ) 25

Double Hashing • Use a second hash function for tries – f(i) = i * h 2(x) • Good choices for h 2(x) ? – Should never evaluate to 0 – h 2(x) = R – (x mod R) • R is prime number less than Table. Size • Previous example with R=7 – h 0(49) = (h(49)+f(0)) mod 10 = 9 (X) – h 1(49) = (h(49)+1*(7 – 49 mod 7)) mod 10 = 6 f(1) 26

Double Hashing Example 27

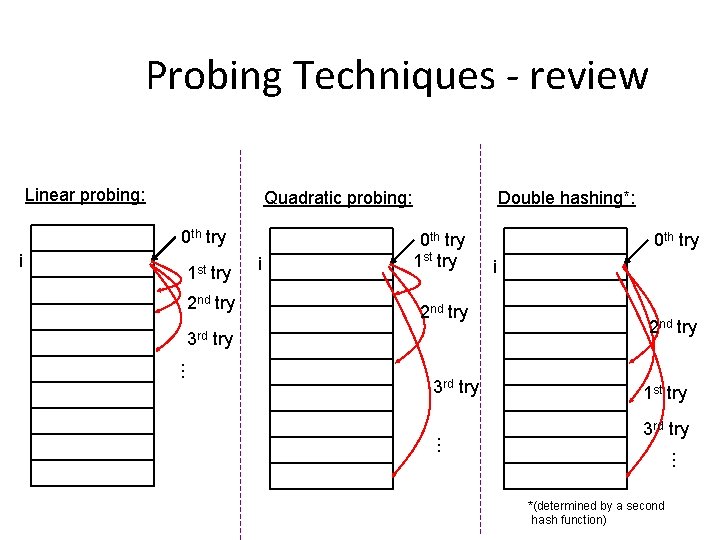
Probing Techniques - review Quadratic probing: 0 th try 1 st try 2 nd try i 0 th try 1 st try 2 nd try 3 rd try … 3 rd … i Double hashing*: 0 th try i 2 nd try 1 st try 3 rd try … Linear probing: *(determined by a second hash function)

Rehashing • Increases the size of the hash table when load factor too high • Typically expand the table to twice its size (but still prime) • Need to reinsert all existing elements into new hash table • When to rehash – When table is half full (λ = 0. 5) – When an insertion fails – When load factor reaches some threshold 29

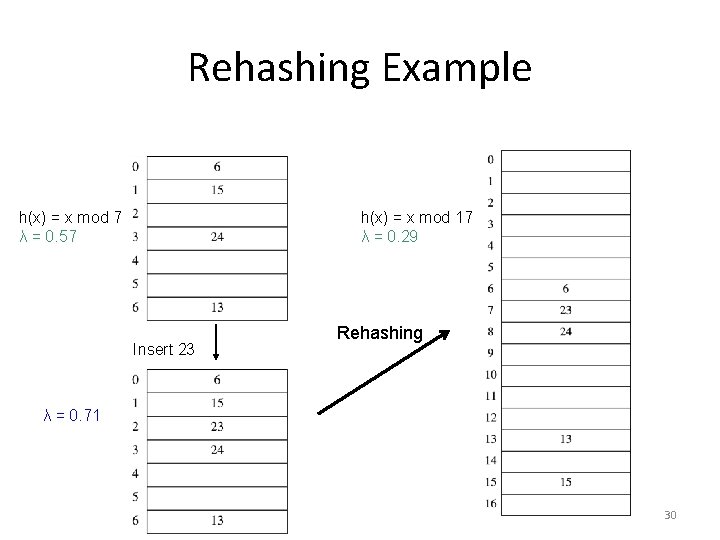
Rehashing Example h(x) = x mod 7 λ = 0. 57 h(x) = x mod 17 λ = 0. 29 Insert 23 Rehashing λ = 0. 71 30

Hash Table Applications • Symbol table in compilers • Accessing tree or graph nodes by name – E. g. , city names in Google maps • Maintaining a transposition table in games – Remember previous game situations and the move taken (avoid re-computation) • Dictionary lookups – Spelling checkers – Natural language understanding (word sense) • Heavily used in text processing languages – E. g. , Perl, Python, etc. 31

Summary • Hash tables support fast insert and search – O(1) average case performance – Deletion possible, but degrades performance • Not suited if ordering of elements is important • Many applications 32

Hashing Problem • Draw the 11 entry hashtable for hashing the keys 12, 44, 13, 88, 23, 94, 11, 39, 20 using the function (2 i+5) mod 11, closed hashing, linear probing • List all identifiers in a hashtable in lexicographic order, using open hashing, the hash function h(x) = first character of x. What is the running time?

End of Hashing 35

Hashing Analysis 36

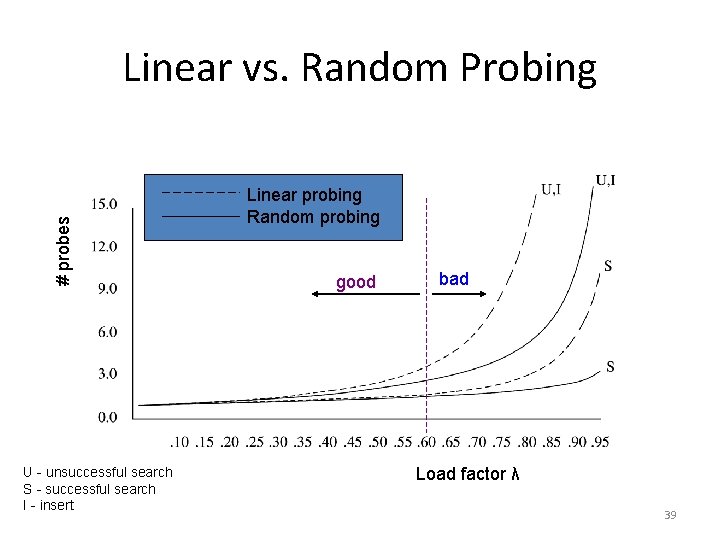
Random Probing: Analysis • Random probing does not suffer from clustering • Expected number of probes for insertion or unsuccessful search: • Example – λ = 0. 5: 1. 4 probes – λ = 0. 9: 2. 6 probes 38

# probes Linear vs. Random Probing U - unsuccessful search S - successful search I - insert Linear probing Random probing good bad Load factor λ 39

Quadratic Probing: Analysis • Difficult to analyze • Theorem 5. 1 – New element can always be inserted into a table that is at least half empty and Table. Size is prime • Otherwise, may never find an empty slot, even is one exists • Ensure table never gets half full – If close, then expand it 40

Double Hashing: Analysis • Imperative that Table. Size is prime – E. g. , insert 23 into previous table • Empirical tests show double hashing close to random hashing • Extra hash function takes extra time to compute 41

Rehashing Analysis • Rehashing takes O(N) time • But happens infrequently • Specifically – Must have been N/2 insertions since last rehash – Amortizing the O(N) cost over the N/2 prior insertions yields only constant additional time per insertion 42

Problem with Large Tables • What if hash table is too large to store in main memory? • Solution: Store hash table on disk – Minimize disk accesses • But… – Collisions require disk accesses – Rehashing requires a lot of disk accesses Solution: Extendible Hashing 43

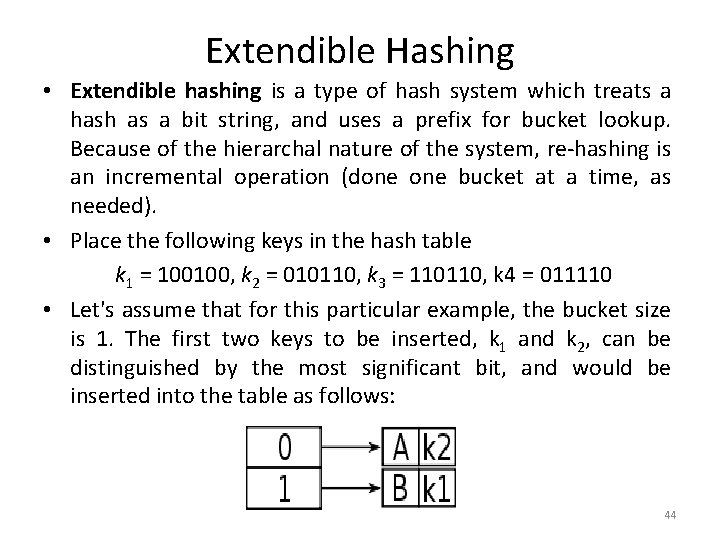
Extendible Hashing • Extendible hashing is a type of hash system which treats a hash as a bit string, and uses a prefix for bucket lookup. Because of the hierarchal nature of the system, re-hashing is an incremental operation (done bucket at a time, as needed). • Place the following keys in the hash table k 1 = 100100, k 2 = 010110, k 3 = 110110, k 4 = 011110 • Let's assume that for this particular example, the bucket size is 1. The first two keys to be inserted, k 1 and k 2, can be distinguished by the most significant bit, and would be inserted into the table as follows: 44

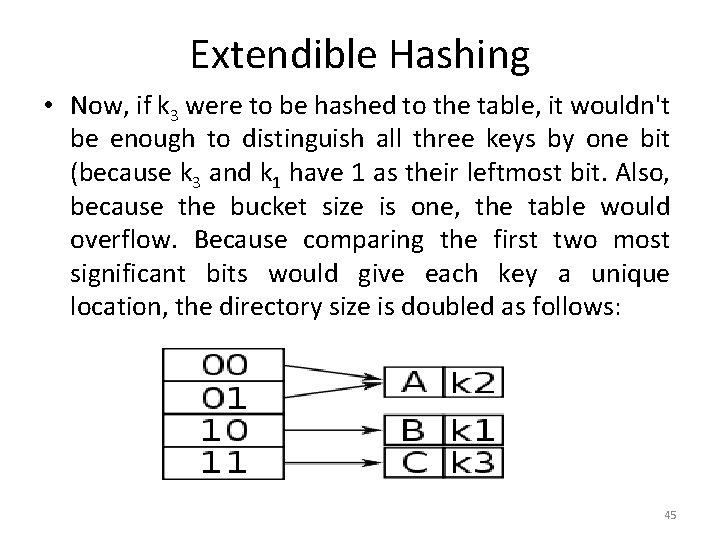
Extendible Hashing • Now, if k 3 were to be hashed to the table, it wouldn't be enough to distinguish all three keys by one bit (because k 3 and k 1 have 1 as their leftmost bit. Also, because the bucket size is one, the table would overflow. Because comparing the first two most significant bits would give each key a unique location, the directory size is doubled as follows: 45

Extendible Hashing • Now, k 4 needs to be inserted, and it has the first two bits as 01. . (1110), and using a 2 bit depth in the directory, this maps from 01 to Bucket A is full (max size 1), so it must be split; because there is more than one pointer to Bucket A, there is no need to increase the directory size. • What is needed is, the information about: – The key size that maps the directory (the global depth), and – The key size that has previously mapped the bucket (the local depth) • In order to distinguish the two action cases: – Doubling the directory when a bucket becomes full – Creating a new bucket, and re-distributing the entries between the old and the new bucket • Back to the two action cases: • If the local depth is equal to the global depth, then there is only one pointer to the bucket, and there is no other directory pointers that can map to the bucket, so the directory must be doubled (case 1). • If the bucket is full, if the local depth is less than the global depth, then there exists more than one pointer from the directory to the bucket, and the bucket can be split (case 2). 46

Extendible Hashing • Key 01 points to Bucket A, and Bucket A's local depth of 1 is less than the directory's global depth of 2, which means keys hashed to Bucket A have only used a 1 bit prefix (i. e. 0), and the bucket needs to have its contents split using keys 1 + 1 = 2 bits in length; in general, for any local depth d where d is less than D, the global depth, then d must be incremented after a bucket split, and the new d used as the number of bits of each entry's key to redistribute the entries of the former bucket into the new buckets. 47

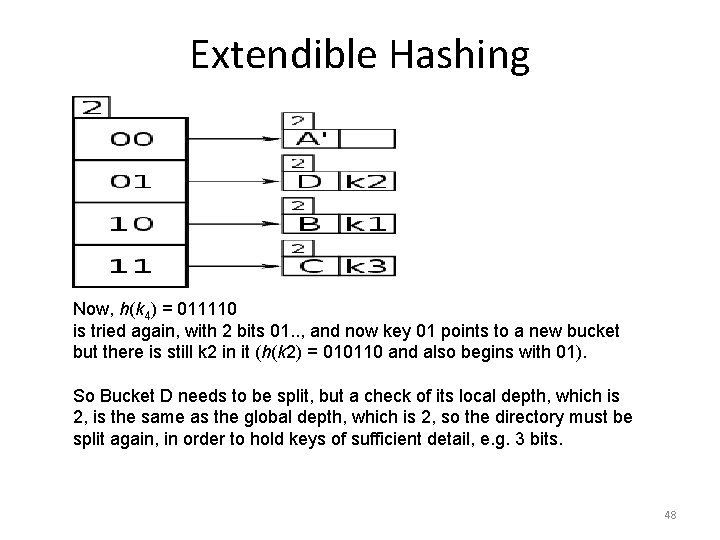
Extendible Hashing Now, h(k 4) = 011110 is tried again, with 2 bits 01. . , and now key 01 points to a new bucket but there is still k 2 in it (h(k 2) = 010110 and also begins with 01). So Bucket D needs to be split, but a check of its local depth, which is 2, is the same as the global depth, which is 2, so the directory must be split again, in order to hold keys of sufficient detail, e. g. 3 bits. 48

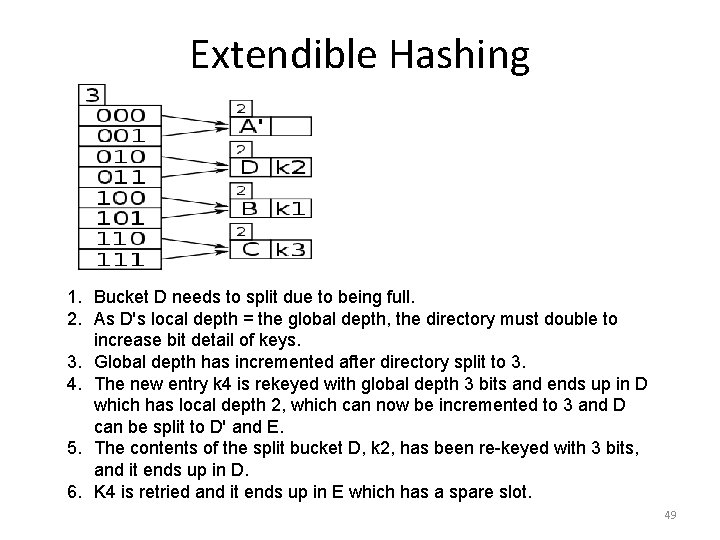
Extendible Hashing 1. Bucket D needs to split due to being full. 2. As D's local depth = the global depth, the directory must double to increase bit detail of keys. 3. Global depth has incremented after directory split to 3. 4. The new entry k 4 is rekeyed with global depth 3 bits and ends up in D which has local depth 2, which can now be incremented to 3 and D can be split to D' and E. 5. The contents of the split bucket D, k 2, has been re-keyed with 3 bits, and it ends up in D. 6. K 4 is retried and it ends up in E which has a spare slot. 49

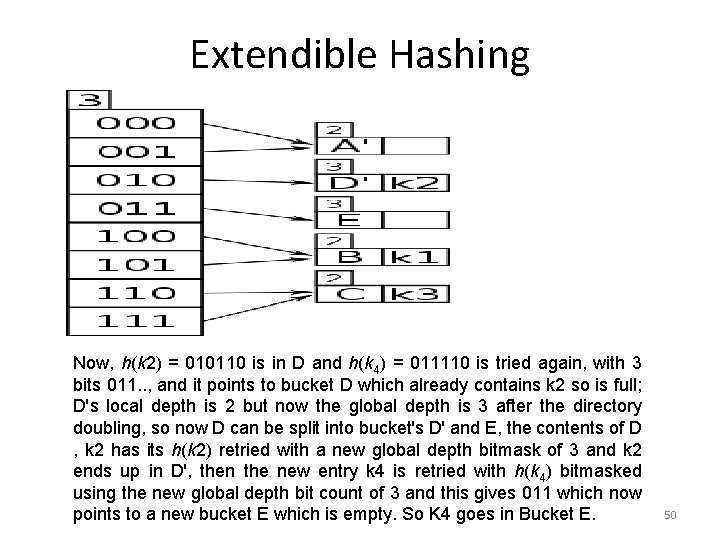
Extendible Hashing Now, h(k 2) = 010110 is in D and h(k 4) = 011110 is tried again, with 3 bits 011. . , and it points to bucket D which already contains k 2 so is full; D's local depth is 2 but now the global depth is 3 after the directory doubling, so now D can be split into bucket's D' and E, the contents of D , k 2 has its h(k 2) retried with a new global depth bitmask of 3 and k 2 ends up in D', then the new entry k 4 is retried with h(k 4) bitmasked using the new global depth bit count of 3 and this gives 011 which now points to a new bucket E which is empty. So K 4 goes in Bucket E. 50