Hashing Motivation n Is there any good structure

Hashing

Motivation n Is there any good structure for searching an element? n n n Sorted list Binary search tree AVL tree … Is it possible to find an element with O(1)? n O(1) means that we know the position of what we want to find n n n Contradiction!! Or, if we can predict, with very high probability, where the element will be, it may be possible. But … how? 2

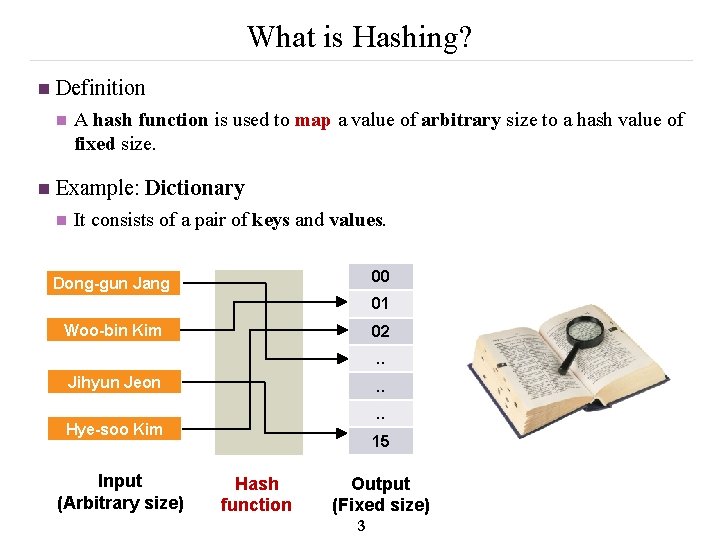
What is Hashing? n Definition n n A hash function is used to map a value of arbitrary size to a hash value of fixed size. Example: Dictionary n It consists of a pair of keys and values. 00 Dong-gun Jang 01 Woo-bin Kim 02. . Jihyun Jeon . . Hye-soo Kim Input (Arbitrary size) 15 Hash function Output (Fixed size) 3

What is Hashing? n Hash Table Key Values 0 1 31 2 112 3 23 4 64 5 205 6 4 7 47 8 8 9 99

What is Hashing? n Hash Table Key Values 0 1 31 2 112 3 23 4 64 5 205 6 5 7 47 8 8 9 99

Good Hash Functions n Which one is better? n The hash function should scatter the elements well enough to be uniformly distributed. n n The hash function should be unbiased. Should use ALL bits in an element. 6

Good Hash Functions n 7

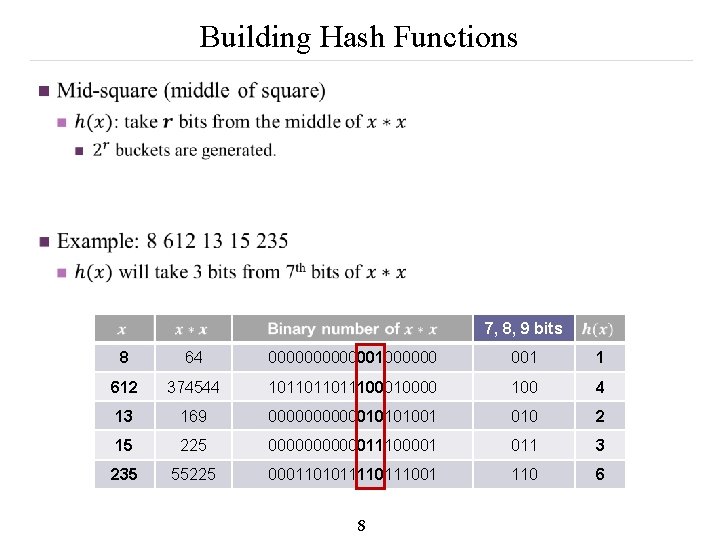
Building Hash Functions n 7, 8, 9 bits 8 64 0000001000000 001 1 612 374544 101101101110000 100 4 13 169 00000010101001 010 2 15 225 00000011100001 011 3 235 55225 00011010111001 110 6 8

Building Hash Functions n 9

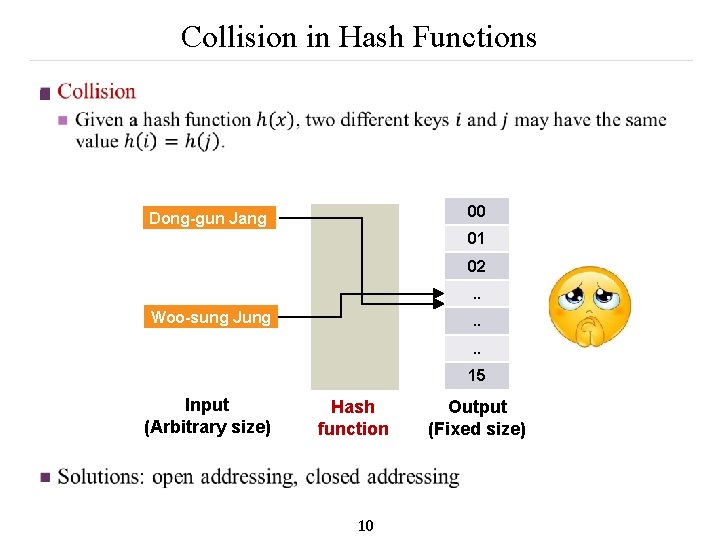
Collision in Hash Functions n 00 Dong-gun Jang 01 02. . Woo-sung Jung . . 15 Input (Arbitrary size) Hash function 10 Output (Fixed size)

Open Addressing: Linear Probing n 0 1 2 3 4 5 6 7 8 9 0 12 1 2 3 12 32 11 4 5 6 7 8 9

Open Addressing: Linear Probing n Key 1 1 2 1 31 3 3 25 25 25 4 5 6 7 8 9 12 25

Open Addressing: Linear Probing n Key 1 1 2 31 31 31 3 3 4 11 11 11 5 25 25 25 62 62 6 7 8 9 13 51

Open Addressing: Linear Probing n Searching: How many buckets are searched? n n Is there 22? 6 buckets Is there 51? 7 buckets Hmm? ? Key n Buckets are linearly searched. n Elements may not be scattered. 1 1 n Elements are easily merged. 2 31 3 3 4 11 5 25 6 62 7 51 How to resolve this problem? n n n Quadratic probing Random probing Rehashing 8 9 14

Open Addressing: Quadratic Probing n 0 1 2 3 12 32 4 5 6 7 8 9 0 62 1 2 3 42 12 32 15 4 5 6 62 7 8 9

Open Addressing: Double Hashing n 16

Open Addressing: Double Hashing n Key 1 2 12 12 3 12 12 62 62 32 32 4 5 32 6 7 8 9 17 42

Closed Addressing: Chaining n Key 1 11 2 22 3 3 31 4 5 6 7 8 9 8 18 51

Performance Analysis for Hashing n 19

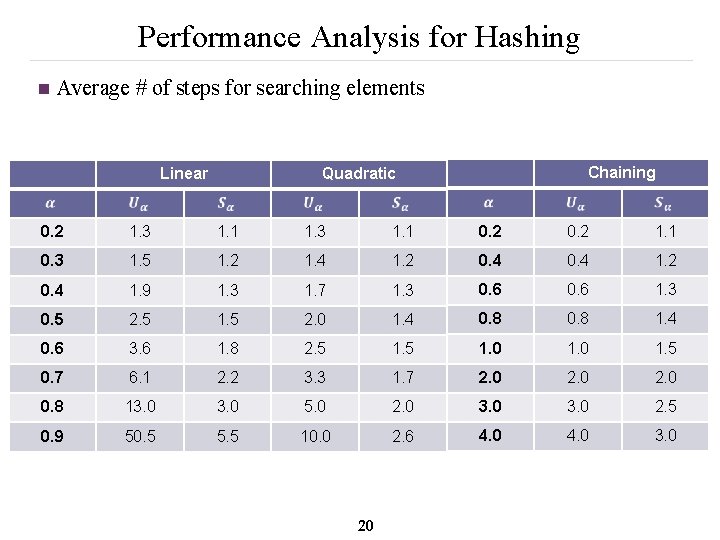
Performance Analysis for Hashing n Average # of steps for searching elements Linear Chaining Quadratic 0. 2 1. 3 1. 1 0. 2 1. 1 0. 3 1. 5 1. 2 1. 4 1. 2 0. 4 1. 9 1. 3 1. 7 1. 3 0. 6 1. 3 0. 5 2. 5 1. 5 2. 0 1. 4 0. 8 1. 4 0. 6 3. 6 1. 8 2. 5 1. 0 1. 5 0. 7 6. 1 2. 2 3. 3 1. 7 2. 0 0. 8 13. 0 5. 0 2. 0 3. 0 2. 5 0. 9 50. 5 5. 5 10. 0 2. 6 4. 0 3. 0 20