Hashbased Signatures Andreas Hlsing PostQuantum Signatures Lattice MQ

Hash-based Signatures Andreas Hülsing

Post-Quantum Signatures Lattice, MQ, Coding Signature and/or key sizes Runtimes Secure parameters 1 -12 -2020 PAGE 2

Hash-based Signature Schemes [Mer 89] Post quantum Only secure hash function Security well understood Fast 1 -12 -2020 PAGE 3

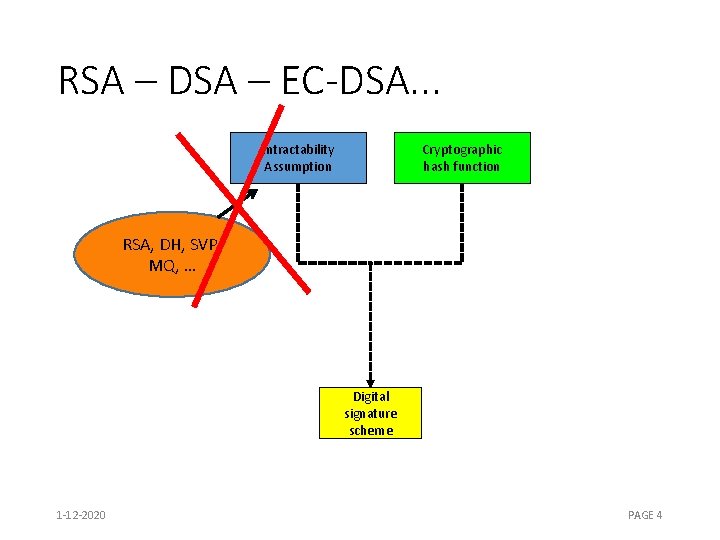
RSA – DSA – EC-DSA. . . Intractability Assumption Cryptographic hash function RSA, DH, SVP, MQ, … Digital signature scheme 1 -12 -2020 PAGE 4

(Hash) function families •

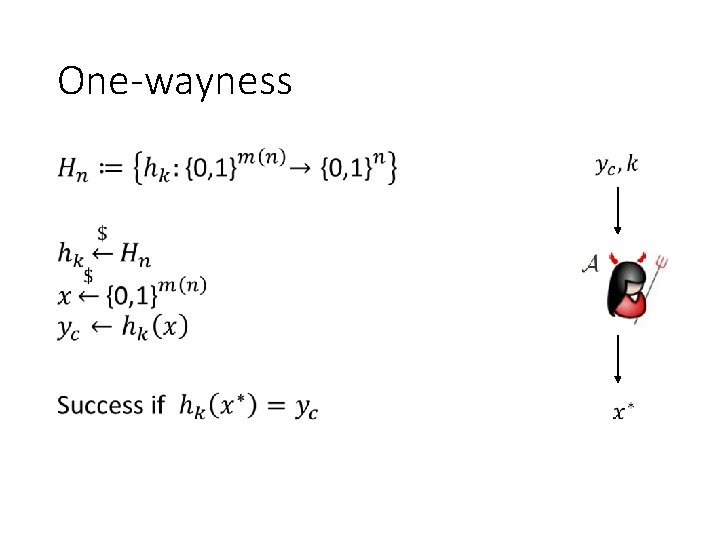
One-wayness •

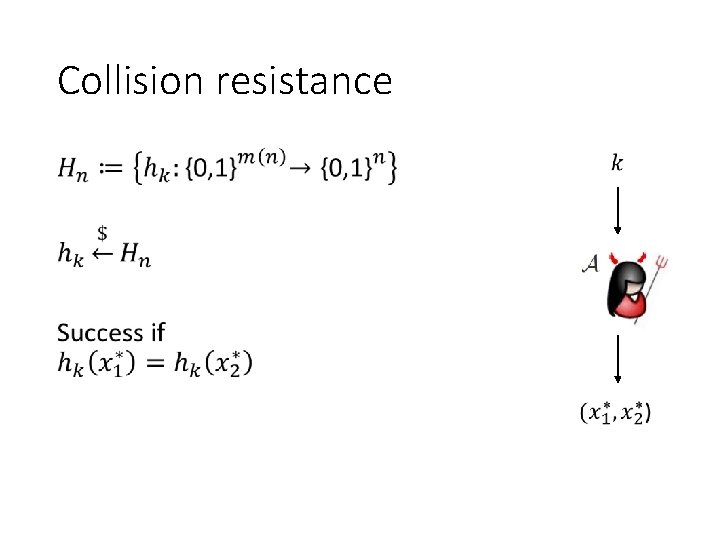
Collision resistance

Second-preimage resistance •

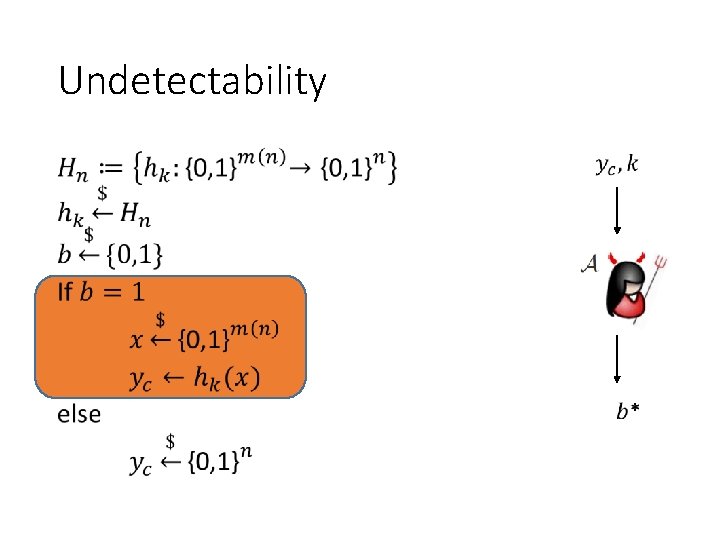
Undetectability •

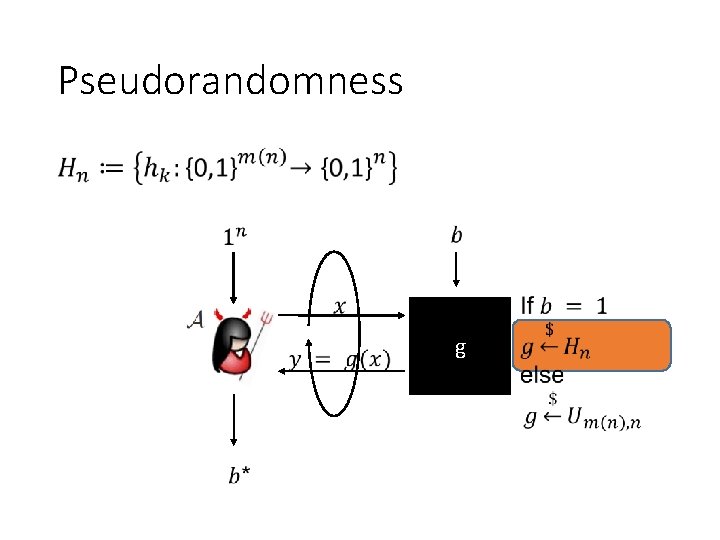
Pseudorandomness • g

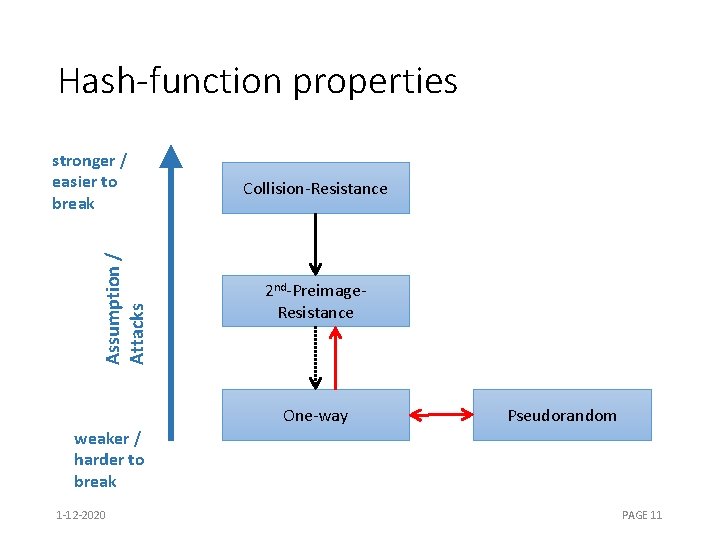
Hash-function properties Assumption / Attacks stronger / easier to break Collision-Resistance 2 nd-Preimage. Resistance One-way Pseudorandom weaker / harder to break 1 -12 -2020 PAGE 11

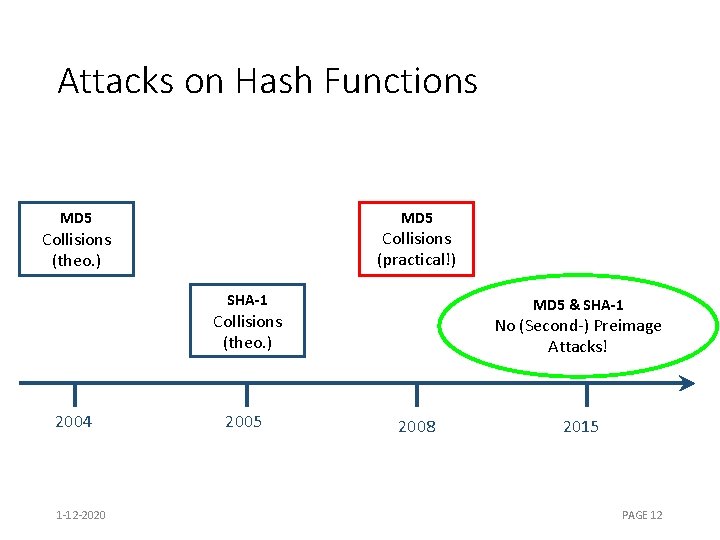
Attacks on Hash Functions MD 5 Collisions (practical!) Collisions (theo. ) SHA-1 MD 5 & SHA-1 Collisions (theo. ) 2004 1 -12 -2020 2005 No (Second-) Preimage Attacks! 2008 2015 PAGE 12

Basic Construction 1 -12 -2020 PAGE 13

Lamport-Diffie OTS [Lam 79] * Message M = b 1, …, bm, OWF H = n bit SK sk 1, 0 sk 1, 1 H PK H pk 1, 0 b 1 Sig 1 -12 -2020 skm, 0 H H pk 1, 1 Mux sk 1, b 1 skm, 1 H H pkm, 0 b 2 Mux bm pkm, 1 Mux skm, bm PAGE 14

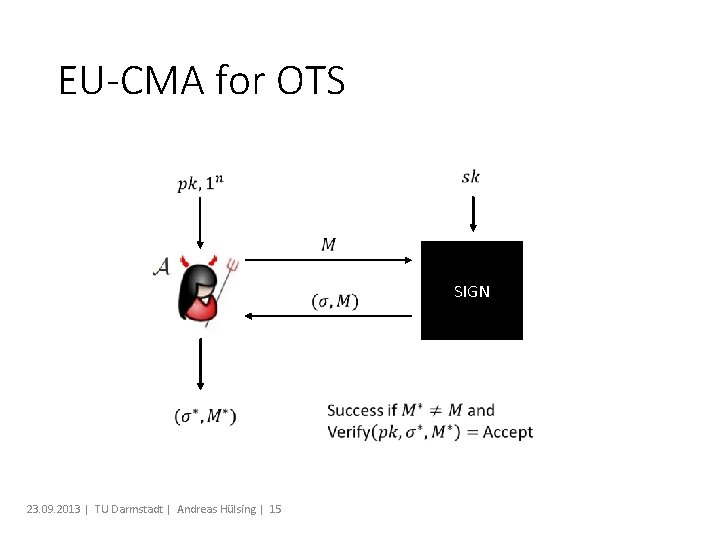
EU-CMA for OTS SIGN 23. 09. 2013 | TU Darmstadt | Andreas Hülsing | 15

Security Theorem: If H is one-way then LD-OTS is one-time eu-cmasecure.

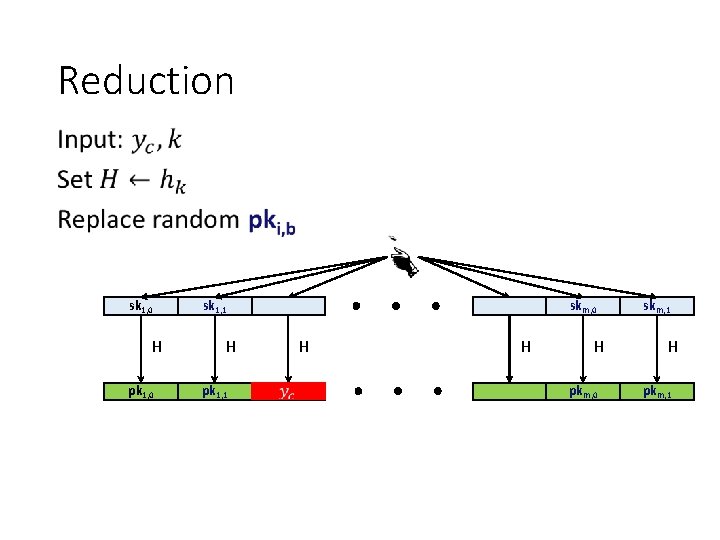
Reduction • sk 1, 0 H pk 1, 0 sk 1, 1 skm, 0 H pk 1, 1 H H H pkm, 0 skm, 1 H pkm, 1

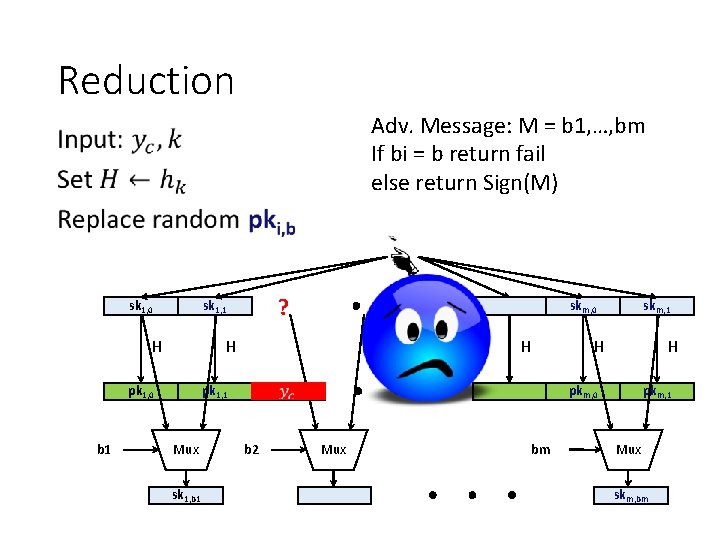
Reduction Adv. Message: M = b 1, …, bm If bi = b return fail else return Sign(M) • sk 1, 0 H skm, 0 H pk 1, 0 b 1 ? sk 1, 1 pk 1, 1 Mux sk 1, b 1 H H H pkm, 0 b 2 skm, 1 Mux bm pkm, 1 Mux skm, bm

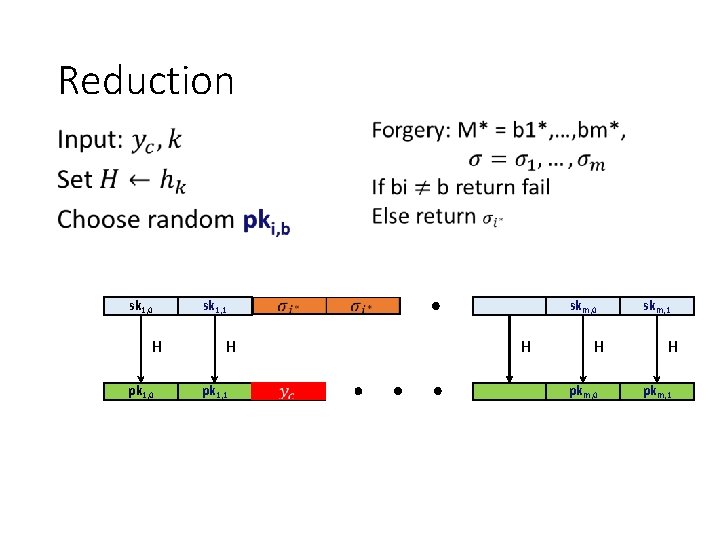
Reduction • sk 1, 0 H pk 1, 0 sk 1, 1 H pk 1, 1 ? skm, 0 H H pkm, 0 skm, 1 H pkm, 1

Reduction - Analysis •

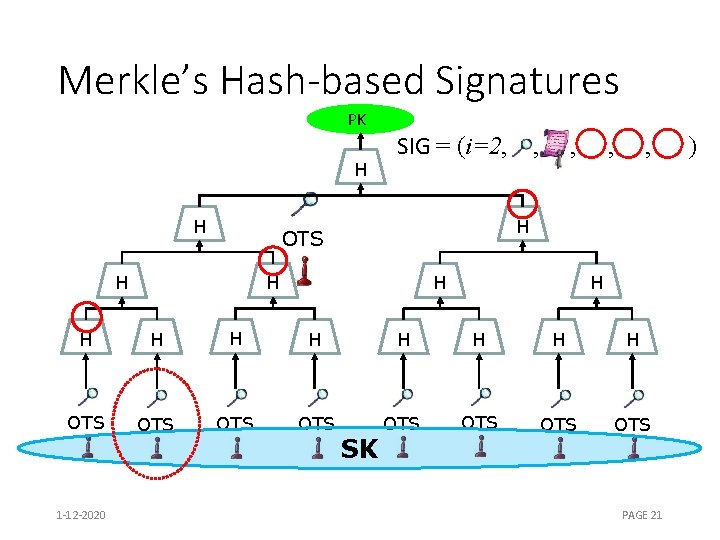
Merkle’s Hash-based Signatures PK H H SIG = (i=2, , H OTS H , H H H OTS OTS 1 -12 -2020 SK PAGE 21 )

Security Theorem: MSS is eu-cma-secure if OTS is a one-time eu-cma secure signature scheme and H is a random element from a family of collision resistant hash functions.

Reduction •

Reduction (Step 4, Extraction) •

Winternitz-OTS

Recap LD-OTS [Lam 79] * Message M = b 1, …, bm, OWF H = n bit SK sk 1, 0 sk 1, 1 H PK Sig H pk 1, 0 b 1 skm, 0 H H H pk 1, 1 Mux sk 1, b 1 skm, 1 H pkm, 0 b 2 Mux bn pkm, 1 Mux skm, bm

LD-OTS in MSS SIG = (i=2, , , ) Verification: 1. Verify 2. Verify authenticity of We can do better!

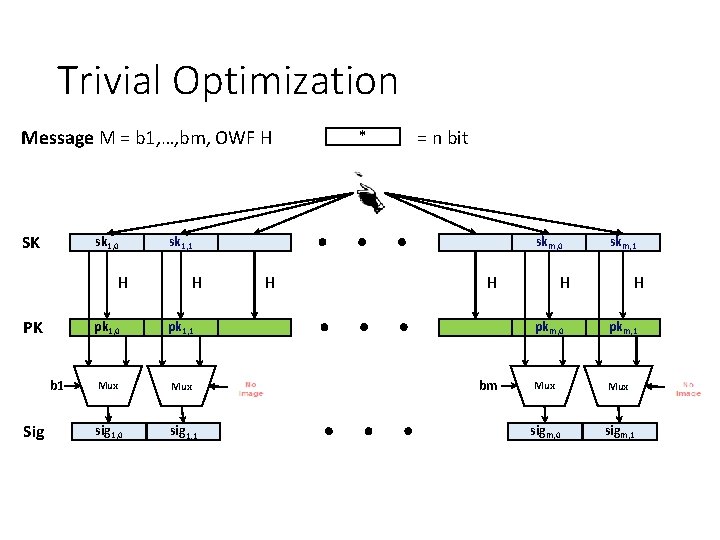
Trivial Optimization * Message M = b 1, …, bm, OWF H = n bit SK sk 1, 0 H PK b 1 Sig sk 1, 1 skm, 0 H pk 1, 0 pk 1, 1 Mux sig 1, 0 sig 1, 1 H H bm skm, 1 H H pkm, 0 pkm, 1 Mux sigm, 0 sigm, 1

Optimized LD-OTS in MSS X SIG = (i=2, , , , Verification: 1. Compute from 2. Verify authenticity of Steps 1 + 2 together verify , )

Germans love their „Ordnung“! Checksum with bad performance!

Optimized LD-OTS

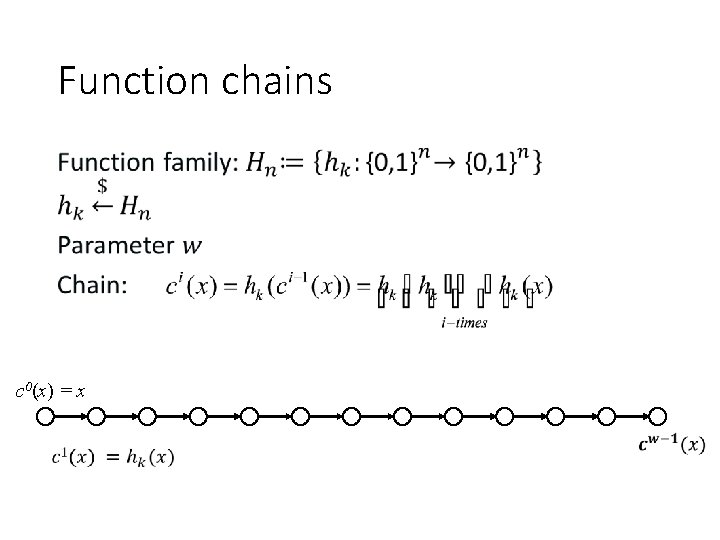
Function chains • c 0(x) = x

WOTS • c 0(sk 1) = sk 1 pk 1 = cw-1(sk 1) c 1(skl ) c 0(skl ) = skl pkl = cw-1(skl )

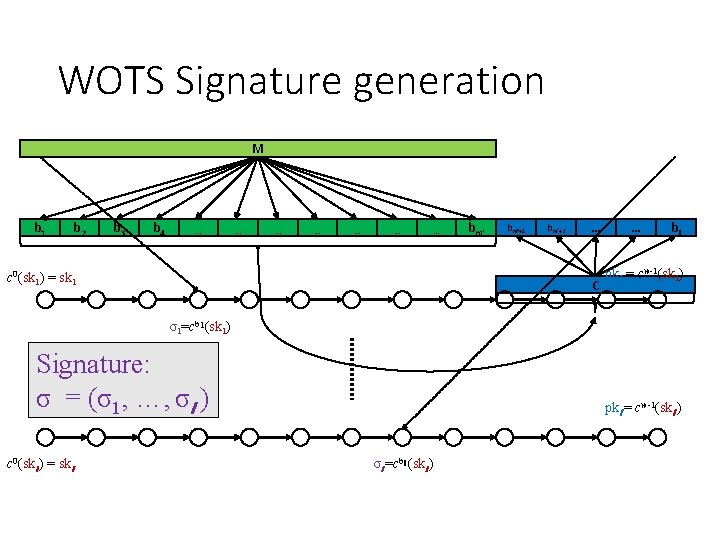
WOTS Signature generation M b 1 b 2 b 3 b 4 … … … … c 0(sk 1) = sk 1 bm‘+1 bm‘+2 … C … bl pk 1 = cw-1(sk 1) σ1=cb 1(sk 1) Signature: σ = (σ1, …, σl ) c 0(skl ) = skl pkl = cw-1(skl ) σl =cbl (skl )

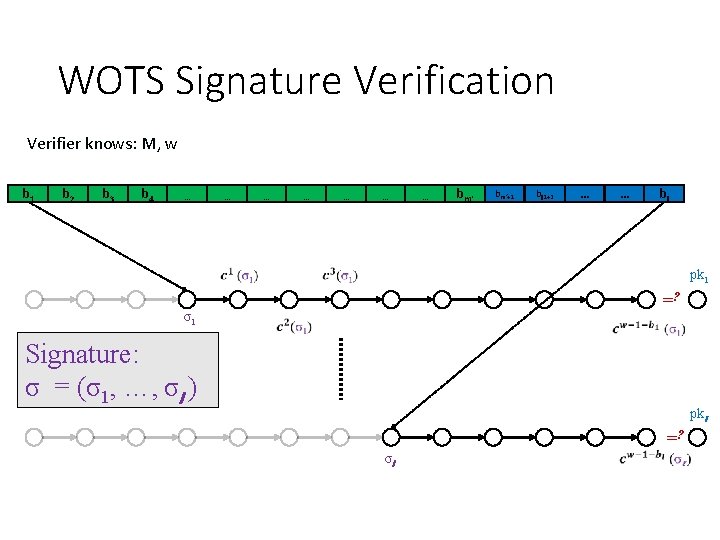
WOTS Signature Verification Verifier knows: M, w b 1 b 2 b 3 b 4 … … σ1 Signature: σ = (σ1, …, σl ) … … … bm‘+1 bl 1+2 … … bl pk 1 =? pkl =? σl

WOTS Function Chains •

WOTS Security •

XMSS

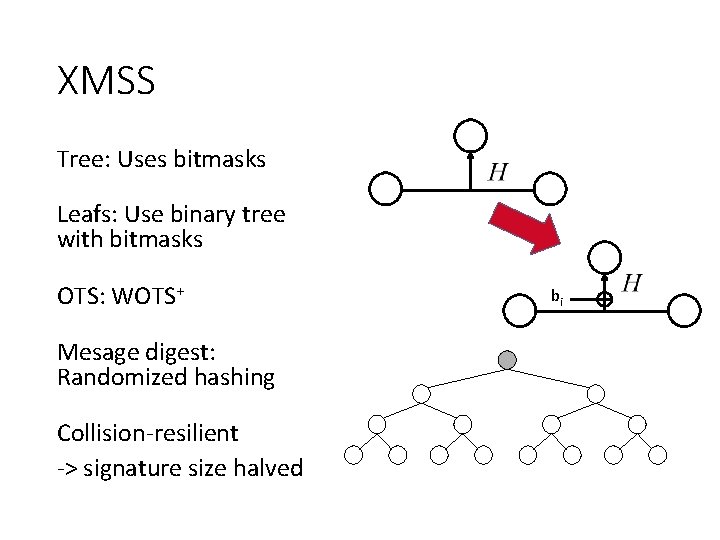
XMSS Tree: Uses bitmasks Leafs: Use binary tree with bitmasks OTS: WOTS+ Mesage digest: Randomized hashing Collision-resilient -> signature size halved bi

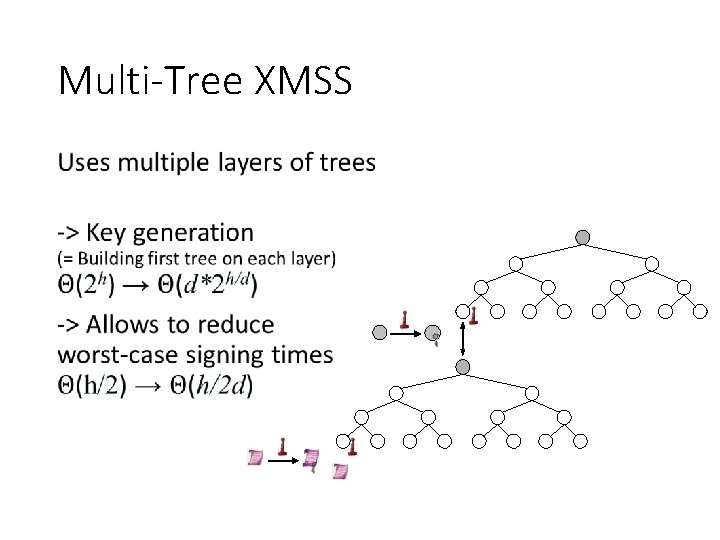
Multi-Tree XMSS •

How to Eliminate the State

Protest? PAGE 43 1 -12 -2020

Few-Time Signature Schemes 1 -12 -2020 PAGE 44

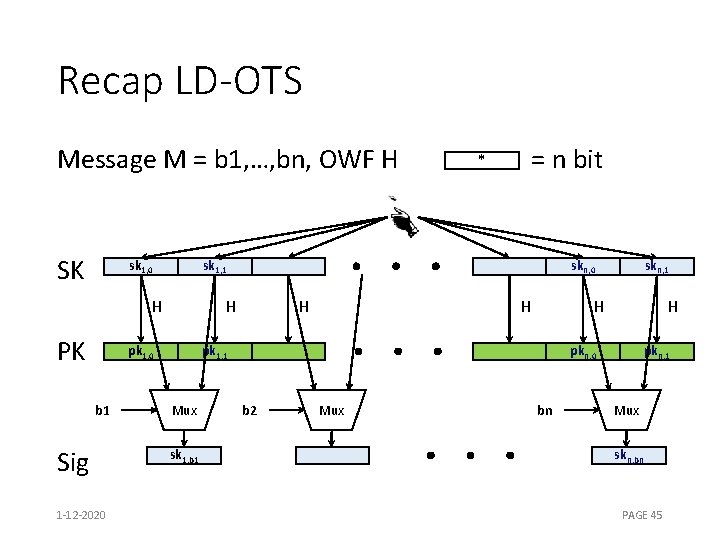
Recap LD-OTS * Message M = b 1, …, bn, OWF H = n bit SK sk 1, 0 sk 1, 1 H PK H pk 1, 0 b 1 Sig 1 -12 -2020 skn, 0 H H H pk 1, 1 Mux sk 1, b 1 skn, 1 H pkn, 0 b 2 Mux bn pkn, 1 Mux skn, bn PAGE 45

HORS [RR 02] * Message M, OWF H, CRHF H’ = n bit Parameters t=2 a, k, with m = ka (typical a=16, k=32) SK sk 1 sk 2 H PK pk 1 skt-1 H pk 1 H H skt H pkt-1 H pkt 1 -12 -2020 PAGE 46

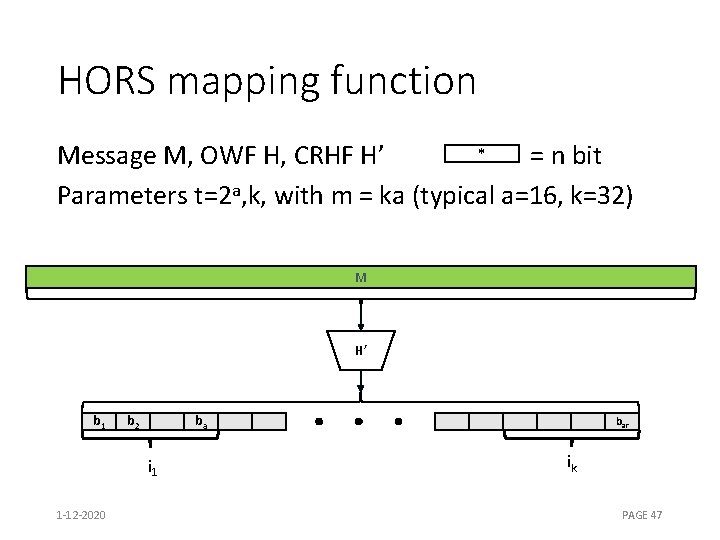
HORS mapping function * Message M, OWF H, CRHF H’ = n bit Parameters t=2 a, k, with m = ka (typical a=16, k=32) M H’ b 1 b 2 ba i 1 1 -12 -2020 bar ik PAGE 47

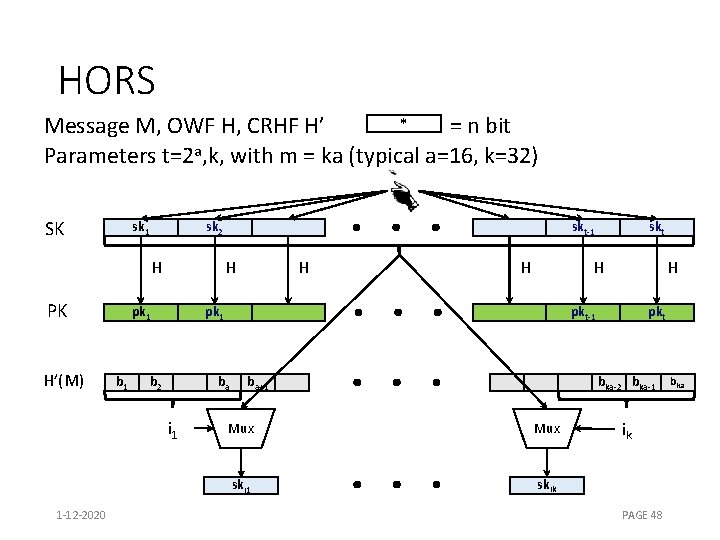
HORS * Message M, OWF H, CRHF H’ = n bit Parameters t=2 a, k, with m = ka (typical a=16, k=32) SK sk 1 sk 2 H PK H’(M) 1 -12 -2020 H pk 1 b 1 skt-1 H H H pk 1 b 2 H pkt-1 ba i 1 skt ba+1 pkt bka-2 bka-1 Mux ski 1 skik ik PAGE 48 bka

HORS Security • 1 -12 -2020 PAGE 49

HORST Using HORS with MSS requires adding PK (tn) to MSS signature. HORST: Merkle Tree on top of HORS-PK • New PK = Root • Publish Authentication Paths for HORS signature values • PK can be computed from Sig • With optimizations: tn → (k(log t − x + 1) + 2 x)n • E. g. SPHINCS-256: 2 MB → 16 KB • Use randomized message hash 1 -12 -2020 PAGE 50

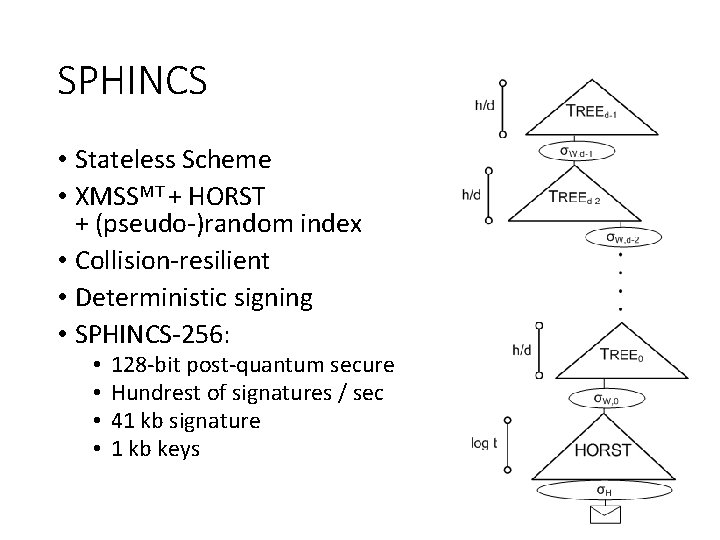
SPHINCS • Stateless Scheme • XMSSMT + HORST + (pseudo-)random index • Collision-resilient • Deterministic signing • SPHINCS-256: • • 128 -bit post-quantum secure Hundrest of signatures / sec 41 kb signature 1 kb keys

Thank you! Questions? For references & further literature see https: //huelsing. wordpress. com/hash-based-signature-schemes/literature/ 1 -12 -2020 PAGE 52