Hash Table Concepts Implementations Hash Table Concepts Implementation

Hash Table Concepts & Implementations

Hash Table Concepts Implementation Sorting by theory

Concepts: hash table & hash function We have seen one way to have a dictionnary. Binary Search Trees 3 types and 2 kinds of implementations • Basic BST • Array • AVL (balanced) • Pointers • Red black (balanced) We’re done with trees. We’ll see another way to have a dictionnary. We have a couple {key, data} and we want: add(key, data) reassign(key, data) remove(key) Hash table lookup(key)

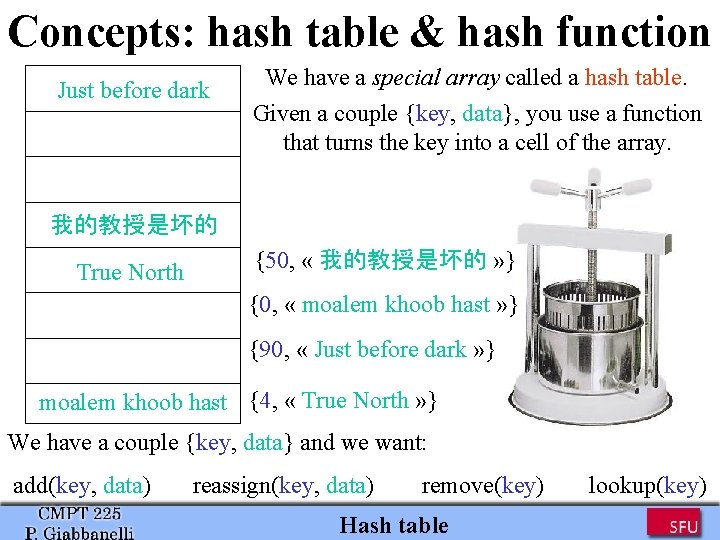
Concepts: hash table & hash function Just before dark We have a special array called a hash table. Given a couple {key, data}, you use a function that turns the key into a cell of the array. 我的教授是坏的 True North {50, « 我的教授是坏的 » } {0, « moalem khoob hast » } {90, « Just before dark » } moalem khoob hast {4, « True North » } 037 4 We have a couple {key, data} and we want: add(key, data) reassign(key, data) remove(key) Hash table lookup(key)

Concepts: hash table & hash function 0 Just before dark 1 2 3 我的教授是坏的 4 True North We have a special array called a hash table. Given a couple {key, data}, you use a function that turns the key into a cell of the array. How can you know if a key is in the hash table? Take the key, turn it into a cell of the array, and look if there is something in that cell. 5 6 7 moalem khoob hast 50 We have a couple {key, data} and we want: add(key, data) reassign(key, data) remove(key) Hash table 3 lookup(key)

Concepts: hash table & hash function In a nutshell A hash table is an implementation of a dictionnary using an array. A hash function transforms the key of an element into its position in the hash table. Hash table

Implementation Content key data Add Lookup Remove Basic. Hash. Table Array of Content Basic. Hashfunction Basic. Hash. Function key position Hash table

Implementation Example: The simplest my way key is of «having Vercingétorix a hash function » . My array is byhas turning a sizethe ofkey 7. I into apply a number and 13%7 by using = 6, the so modulo it will gotointo make theit 6 th fit in cell. a small array. Hash table

Implementation When I create my hash function, I tell it what’s the size of the array so it can do the modulo accordingly. To add something, get its position and just insert it. To know if an element is inside, check if its position is used. Then we save the data, empty the cell and return the data. Hash table We cannot access the data of something null so we first check if the cell is used.

Implementation Now that it has been implemented, we must DEBUG!!! As all basic structures, you have it available from Java, so use it. http: //java. sun. com/j 2 se/1. 5. 0/docs/api/java/util/Hashtable. html Hash table

Concepts Hash function Lets say that our keys are words of at most 13 characters. 13 That’s 26 possible values… Since the hash table is smaller, it means that two (or more) keys may have the same position. When it happens, we say that we have a collision. Hash table

Concepts You’re taking the train and you have a ticket with your seat number. Some people actually don’t give a damn about the tickets and they sit how do you find a seat? where they feel like. So, aaaaaaaaaaaaaaa Hash table

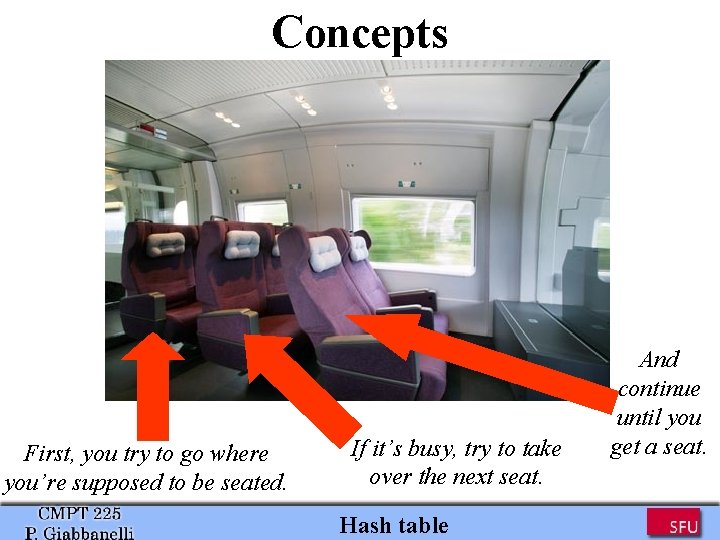
Concepts First, you try to go where you’re supposed to be seated. If it’s busy, try to take over the next seat. Hash table And continue until you get a seat.

Concepts In a nutshell A collision happens when two keys are assigned the same position. Resolving a collision means that we look for a free location to be assigned to the newcoming key. Linear probing resolves a collision by a sequential search. Hash table

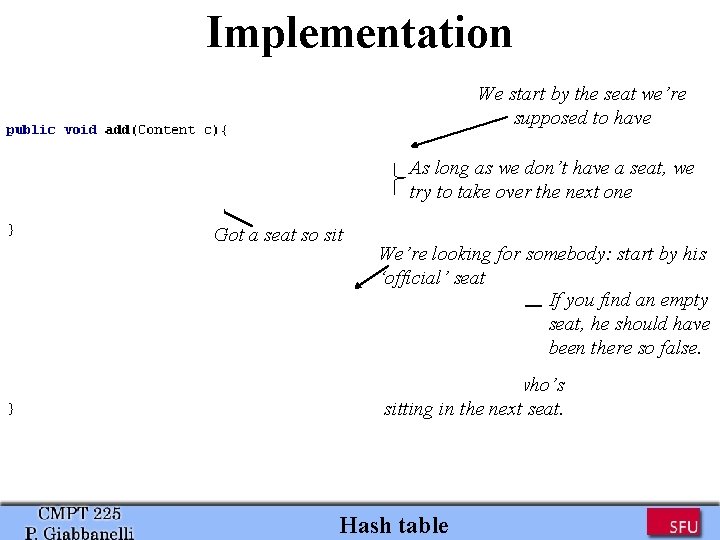
Implementation We start by the seat we’re supposed to have As long as we don’t have a seat, we try to take over the next one Got a seat so sit We’re looking for somebody: start by his ‘official’ seat If you find an empty seat, he should have been there so false. Otherwise, look who’s sitting in the next seat. Hash table

Implementation Hash function: f(x) = x % 5 Add: {7, « Busy » } Add: {2, « Bee » } Add: {1, « Big » } Add: {36, « Bitching » } 0 1 Big 1 7 Busy 2 2 Bee 3 Hash table 31 Bitching 4

Implementation Lookup(2) Lookup(4) Previously, we removed an element by just setting it to null. But if we do this, it creates problems for the probe. Lookup(2) Incorrect since 2 is in! 0 1 Big 1 7 Busy 2 2 Bee 3 Hash table 31 Bitching 4

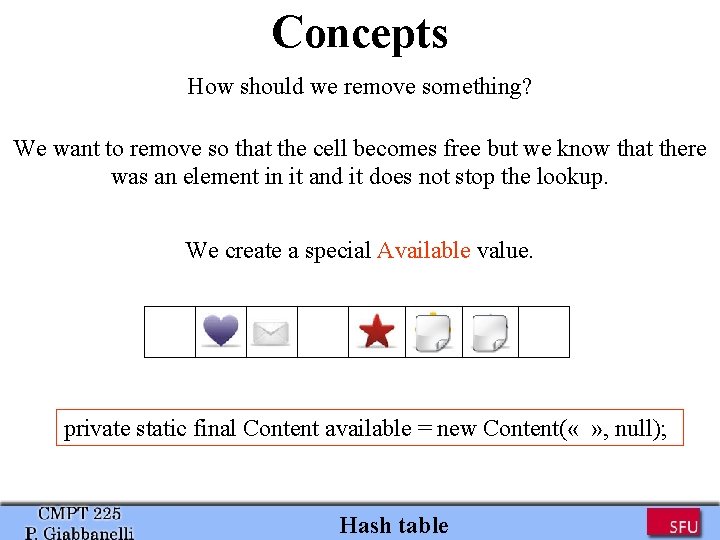
Concepts How should we remove something? We want to remove so that the cell becomes free but we know that there was an element in it and it does not stop the lookup. We create a special Available value. private static final Content available = new Content( « » , null); Hash table

Implementation We only continue if we cannot add: the position is not empty or not available. What should we change to lookup? Nothing. We know it’s in so search until you get it. Then save the data, make the cell available, and return the data. Hash table

Concepts When you use linear probing, it solves your problem but it’s making it worst for the next time. Indeed, there will be a high probability that if you have one collision then you will have more. We see… More probing! Yet you’ll earn $ and be happy Hash table

Concepts When you use linear probing, it solves your problem but it’s making it worst for the next time. Indeed, there will be a high probability that if you have one collision then you will have more. Instead of a linear probing that adds i, we can try quadratic with i². 0 1 2 Braided Hash function: f(x) = f % 7 Linear probing: 4 3 Creek 4 Livingston Add {10, Creek} Add {3, Livingstone} Add {17, Suite} Add {2, Braided} Add {16, Jim} Hash table 5 Suite 6 Jim

Concepts When you use linear probing, it solves your problem but it’s making it worst for the next time. Indeed, there will be a high probability that if you have one collision then you will have more. Instead of a linear probing that adds i, we can try quadratic with i². 0 Suite 1 2 Braided Hash function: f(x) = f % 7 Linear probing: 4 Quadratic probing: 2 3 Creek 4 Livingston Add {10, Creek} Add {3, Livingstone} Add {17, Suite} Add {2, Braided} Add {16, Jim} Hash table 5 6 Jim

Concepts In a nutshell Linear probing tends to create clusters: a contiguous group of elements. Quadratic probing offers a better spacing, i. e. it reduces the likeliness that one collision is followed by many. There are other probes… Hash table