Hash Maps ARRAY SIZE AND HASH FUNCTIONS 1

Hash. Maps: ARRAY SIZE AND HASH FUNCTIONS 1

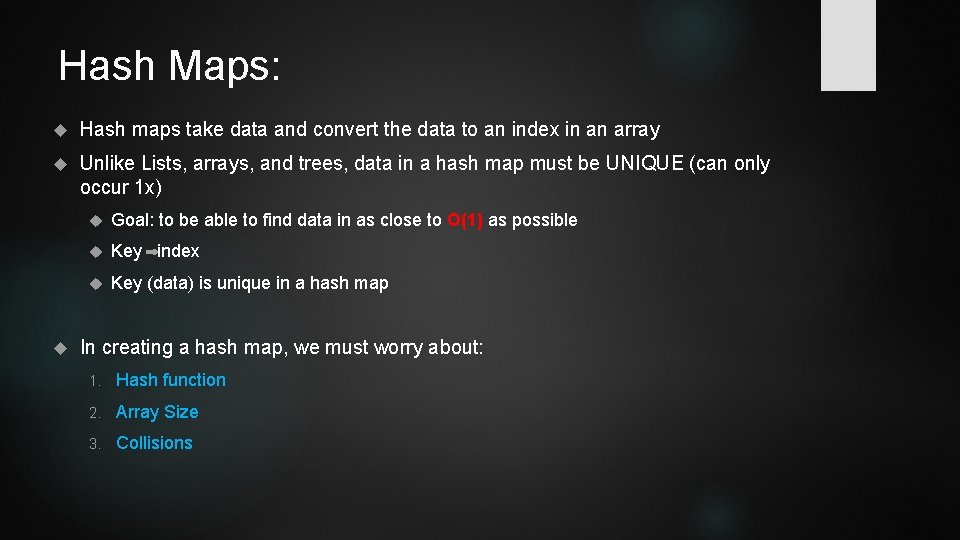
Hash Maps: Hash maps take data and convert the data to an index in an array Unlike Lists, arrays, and trees, data in a hash map must be UNIQUE (can only occur 1 x) Goal: to be able to find data in as close to O(1) as possible Key index Key (data) is unique in a hash map In creating a hash map, we must worry about: 1. Hash function 2. Array Size 3. Collisions

1. Hashing Function A good hash function: Maps all keys (data) to indices within the array! Distributes keys evenly throughout array Avoids collisions Two keys mapping to the same index Computes quickly Computes consistently Note: There are many hash functions. Some are better than others. None are perfect… yet…

Potential Hash functions: Key – anything that is unique about the data Could just take the key (which can be represented as a number – this is the computer) and then mod with arraysize E. g. , student. id % array. Size Problem: Could end up with many numbers hashing to the same value x: 71 i: 1 x: 81 i: 1 x: 75 i: 5 x: 89 i: 9 x: 29 i: 9 x: 99 i: 9 x: 72 i: 2 E. g. , array is 100 and keys are all multiples of 10 0 1 2 81 72 3 4 5 75 6 7 8 9 79

2. Better Hash Functions: Array Size Hash functions and array size are intricately connected. We know: we’re not going to be able to fill the array perfectly we’ll have some unfilled spaces We know: the last step in the hash function has to be mod-ing by the array size… So: pick a good array size! Make it a prime number

2. Better Hash Functions: Array Size Hash functions and array size are intricately connected. Pick a prime number for the array size! works better with larger primes that aren’t close to powers of 2) E. g. , 8 random numbers between 0 and 100, hash function is number%11: x: 71 i: 5 x: 81 i: 4 0 1 2 x: 75 i: 9 99 89 79 x: 89 i: 1 x: 29 i: 7 x: 99 i: 0 x: 79 i: 2 x: 72 i: 6 Already we’ve got a better hash function… Even better: double the amount of data, then to go the next largest prime 3 4 5 6 7 81 71 72 29 8 9 75 10

Hash Functions: There are many, many hashing functions You can come up with your own… Remember: Quick to calculate Evenly distributes keys within a range Consistently map a key to an index Could add the digits in a number and mod by array size Could just take any number in the key and mod by the array size Remember – any pattern or trend in the numbers could lead to uneven distribution of indices

Possible hash functions on ints: Power hash: take the integer, take each digit in the integer to the power of its place in ascending order: E. g. , 324 = 3^1 + 2^2 + 4^3 = 3+4+12 = 19 % arraysize Middle r: square int, (possibly convert to binary), and use the middle r bits or numbers (then mod by array size) E. g. , 442=1936, maybe take the middle 2 numbers, so you’d have 93 % arraysize Folding: divide the number to equal sized pieces and add the pieces (then mod by arraysize) Works best with smaller numbers… (e. g. , 328 -444 -2870 becomes (32 +84 + 44+28+70 )%arraysize MANY hashing functions involve shifting bits…