Hash Function 1 Contents Hash Functions Dedicated Hash

Hash Function 1

Contents Hash Functions Dedicated Hash Functions ◦ Useful for lightweight authentication in RFID system Message Authentication Codes ◦ CBC-MAC ◦ Nested MAC Collusion Search Attacks 2

Hash function q Compress a binary string with an arbitrary length into a fixed short message q Used for digital signature, integrity, authentication, etc. {0, 1}d h() {0, 1}r d>r hash, hash code/value/result message digest, checksum, MIC, authentication tag, seal, compression digital fingerprint, imprint 3

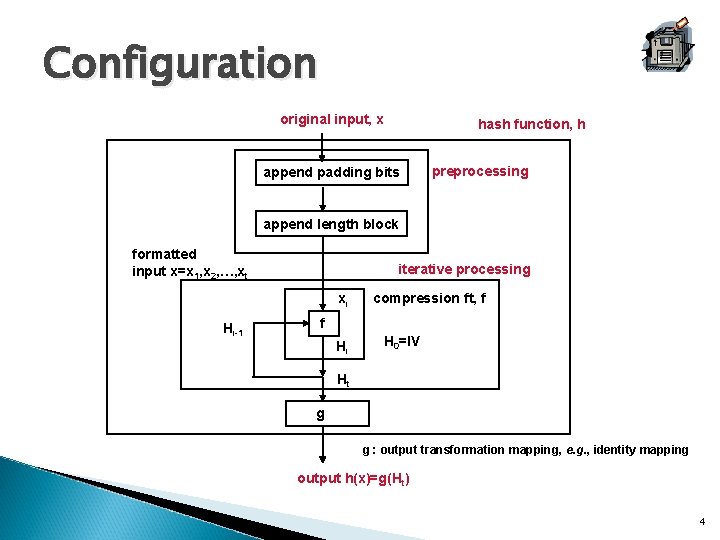
Configuration original input, x hash function, h append padding bits preprocessing append length block formatted input x=x 1, x 2, …, xt iterative processing xi Hi-1 compression ft, f f Hi H 0=IV Ht g g : output transformation mapping, e. g. , identity mapping output h(x)=g(Ht) 4

Requirements Compression One-wayness ◦ Preimage resistance: Given y, it is computationally infeasible to compute x with y=h(x) ◦ Second Preimage resistance: Given x and h(x), it is computationally infeasible to compute x’ with h(x)=h(x’) Collision-free (Prevent internal misuse) : It is computational infeasible to find a pair (x, x’), x x’ satisfying h(x)=h(x’). Efficiency ◦ Easy to compute h(x) for a given x. 5

Relationship Collision resistance (which means collusion can’t be efficiently solved) implies 2 nd-preimage resistance Collision resistance does not guarantee preimage resistance ◦ ◦ ◦ Let g be a collision resistance hash function to n-bit output h= 1 || x, if x has bitlength n h= 0 || g(x), otherwise h is collision resistant with n+1 bit hash not preimage resistant to find an image easily 6

Classification Using key or not ◦ Keyed hash : MAC (Message Authentication Code) ◦ Un-keyed hash : MDC (Manipulation Detection Code) OWHF(One Way Hash Function) CFHF(Collision-Free Hash Function) What purpose ◦ MAC Block Cipher-Based (DES-CBC MAC) Hash Function-Based(HMAC) ◦ MDC Dedicated Hash Functions (MD class, SHS, HAVAL) Block Cipher-Based (MDC-2, MDC-4) Modular Arithmetic: MASH-1, MASH-2 7

Random Oracle Model (ROM) Model for ideal hash function H() behave like a random function ◦ If H() is fixed, invalid assumption ◦ Whenever H() is used, we call oracle for the random function (black box containing random ft. ) Good for screening insecure solutions Security under ROM implies to many (not all !) attack Not a complete proof of security, but a good argument / evidence of security : vs. standard model 8

MAC forgery Universal forgery : Adversary can find the equivalent algorithm as MAC function Selective forgery : Adversary can create a pair of new text-MAC. Existential forgery : Even if adversary can’t adjust the value of text, he can create a pair of new text-MAC. 9

Birthday Paradox Probability that 2 persons have the same birthday among r persons : pr (Assumption) each birthday is independent and uniform in the range 1 to m. 2/(2 m) r r r -r pr=1 -(m) / m =1 - m! / m (m-r)! ≈ √ e where, (m)r = m(m-1)…(m-r+1) If r= √m, pr ≈ 0. 5 , e. g. , m=365, r=23, pr>0. 5 ↔ n-bit hash function will collide with probability 0. 5 after √ (2 n) times operation 10

Design Criteria All input value must affect to compute the hashed value. (Ex) Crytanalysis of Snefru No trapdoor The length of hashed value must be greater than 128 bit guarantee breaking complexity 264 by brute force attack. ◦ 1 month with 10 M $ machine in ‘ 94 ◦ Expected cost today : less than 100, 000$ Maximum error propagation from input to output. 11

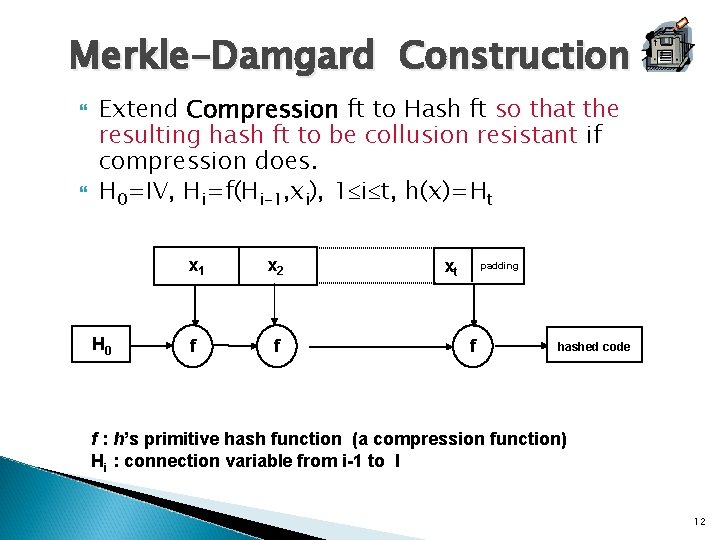
Merkle-Damgard Construction Extend Compression ft to Hash ft so that the resulting hash ft to be collusion resistant if compression does. H 0=IV, Hi=f(Hi-1, xi), 1 i t, h(x)=Ht H 0 x 1 x 2 f f xt padding f hashed code f : h’s primitive hash function (a compression function) Hi : connection variable from i-1 to I 12

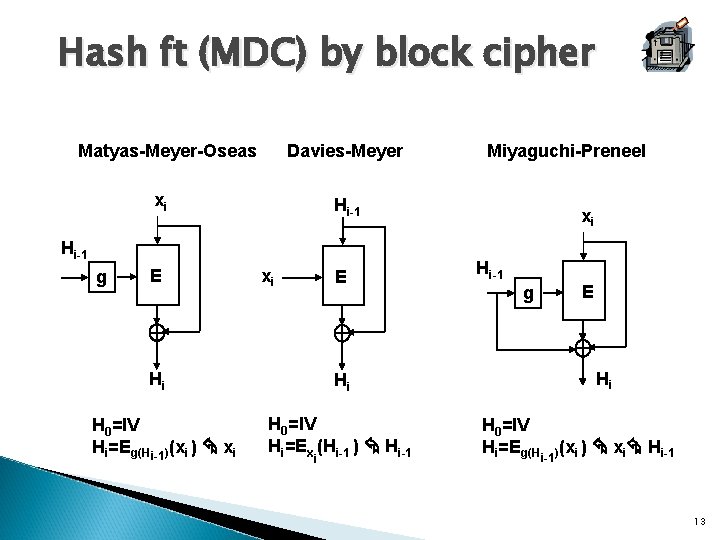
Hash ft (MDC) by block cipher Matyas-Meyer-Oseas Davies-Meyer xi Hi-1 g E xi E Hi H 0=IV Hi=Eg(Hi-1)(xi ) xi Miyaguchi-Preneel Hi H 0=IV Hi=Ex (Hi-1 ) Hi-1 i xi Hi-1 g E Hi H 0=IV Hi=Eg(Hi-1)(xi ) xi Hi-1 13

Comparison Hash Function Matyas-Meyer-Oseas Davis-Meyer Miyaguchi-Preneel (n, k, m) (n, k, n) MDC-2 (w/DES) (64, 56, 128) MDC-4(w/DES) (64, 56, 128) Rate (k/m) 1 k/n 1 ½ 1/4 Yield m-bit hash using n-bit block cipher with k -bit key All of them are secure assuming a block cipher satisfies required randomness properties 14

Hash by modular operation MASH: Modular Arithmetic Secure Hash algorithm Weakness: Efficiency (and Insecurity) Quadratic Congruential ◦ Hi = (xi + Hi-1)2 mod N, H 0=0 where N=Mersenne prime 231 -1 ◦ Hi = (xi Hi-1)2 mod N xi ◦ Hi = (xi Hi-1)e mod N 15

Dedicated Hash Functions 16

MD 4(I) Preprocessing a message, x 1. Padding: d =(447 -|x|) mod 512 2. Length of a message: n= |x| mod 264, |n|=64 bit 3. M = x ||1||0 d||n multiple of 512 where || denotes concatenation * little-endian : W=224 B 4+216 B 3+28 B 2+B 1 (B 1: lowest address) 17

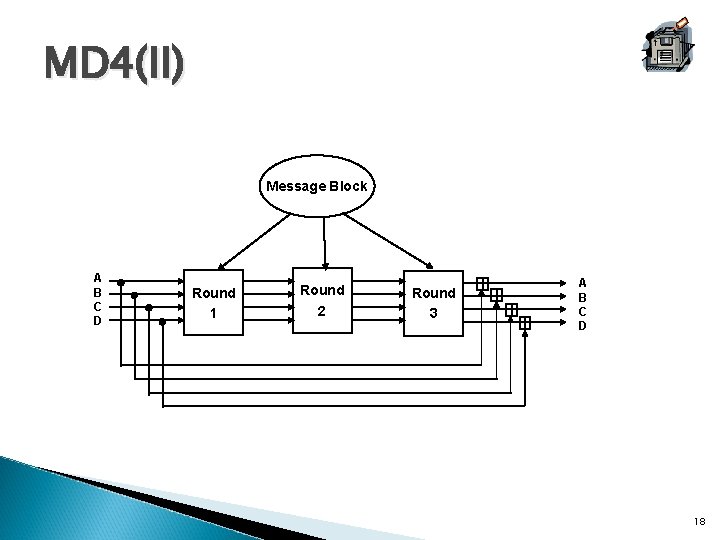
MD 4(II) Message Block A B C D Round 1 Round 2 Round 3 A B C D 18

Round 1 in MD 4 1. 2. 3. 4. 5. A=(A+f(B, C, D)+X[0])<<<3 D=(D+f(A, B, C)+X[1])<<<7 C=(C+f(D, A, B)+X[2])<<<11 B=(B+f(C, D, A)+X[3])<<<19 A=(A+f(B, C, D)+X[5])<<< 3. . 16. B=(B+f(C, D, A)+X[15])<<<19 where, f(X, Y, Z) = (X Y) (( X) Z) , : OR, : AND, : complement, <<<s : circular left rotate by s 19

Pseudocode of MD 4 1. Preprocess: M is 512 * N bits (512 bits=16 words) 2. Define 32 bits constants: A=67452301 h, B=efcdab 89 h, C=98 badcfeh, D=10325476 h 3. for i=0 to N/16 -1 do (N mod 16=0) 3 -1. for j=0 to 15 do X[j] =M[16 i+j] (M[i] : 32 bit string) 3 -2. AA=A, BB=B, CC=C, DD=D 3 -3. Round 1(for j=0. . 15), Round 2(for j=16. . 31), Round 3(j=32. . 47) 3 -4. A=A+AA, B=B+BB, C=C+CC, D=D+DD where + is modular addition over 232. 4. output A||B||C||D|| 20

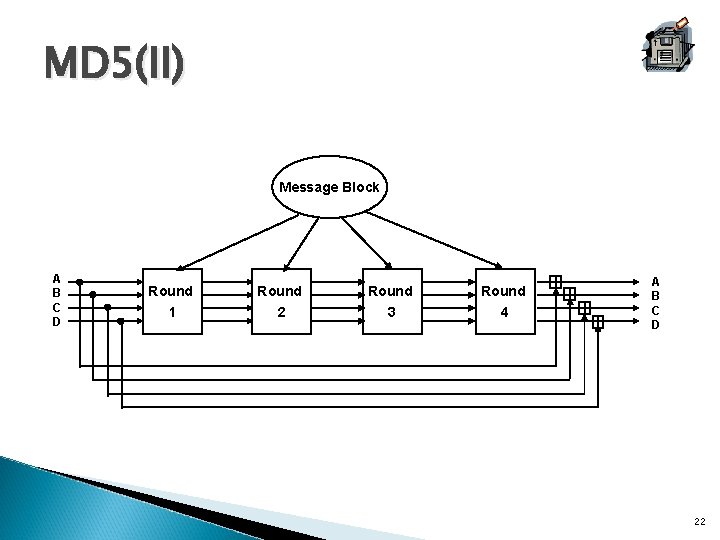
MD 5(I) Add 4 -th rounds (16 steps) in MD 4 Change g function in 2 round from symmetric ft (X Y) v (X Z) v (Y Z) to non-symmetric ft (X Z) v (Y ( Z)) Modify the access order for message words in Rounds 2 and 3 Modify the shift amounts Use unique constants in each of the 4 16 steps Each step is added to the output of a previous step to achieve avalanche effect as earlier as possible. 21

MD 5(II) Message Block A B C D Round 1 Round 2 Round 3 Round 4 A B C D 22

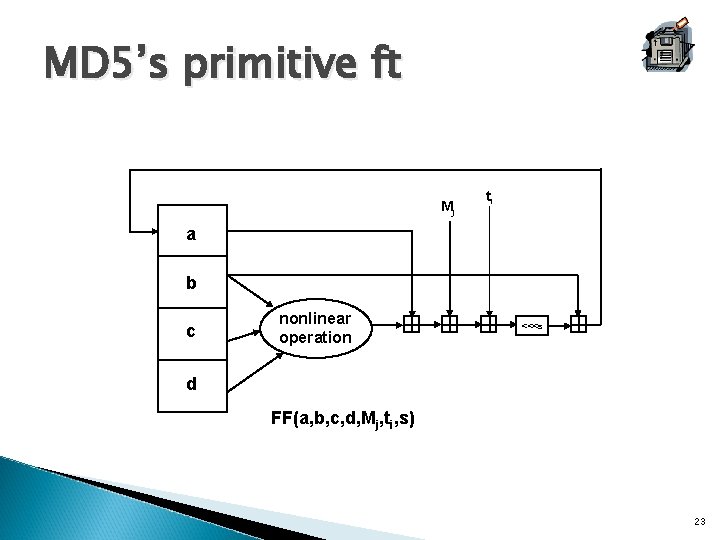
MD 5’s primitive ft Mj ti a b c nonlinear operation <<<s d FF(a, b, c, d, Mj, ti, s) 23

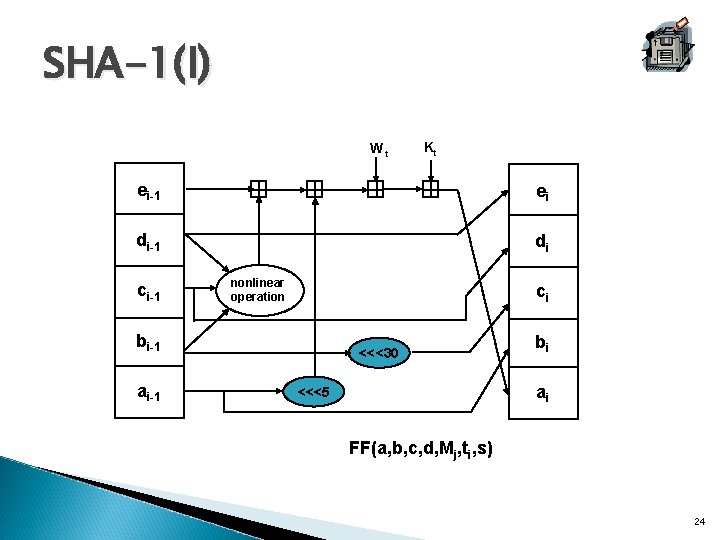
SHA-1(I) Wt Kt ei-1 ei di-1 di ci-1 nonlinear operation ci bi-1 ai-1 <<<30 bi ai <<<5 FF(a, b, c, d, Mj, ti, s) 24

SHA-1(II) 160 bit hashed value (5 words), Big-endian 4 round hash, each round has 20 step Change internal primitive ft and constants (B Ft(B, C, D) = B (B B C) v (( B) D) C D 0 ≤ t ≤ 19 20 ≤t ≤ 39 40 ≤t ≤ 59 60 ≤t ≤ 79 Secure Hash Standard(SHS), FIPS Pub 180 -1, 1995. For details, refer to p. 138. 25

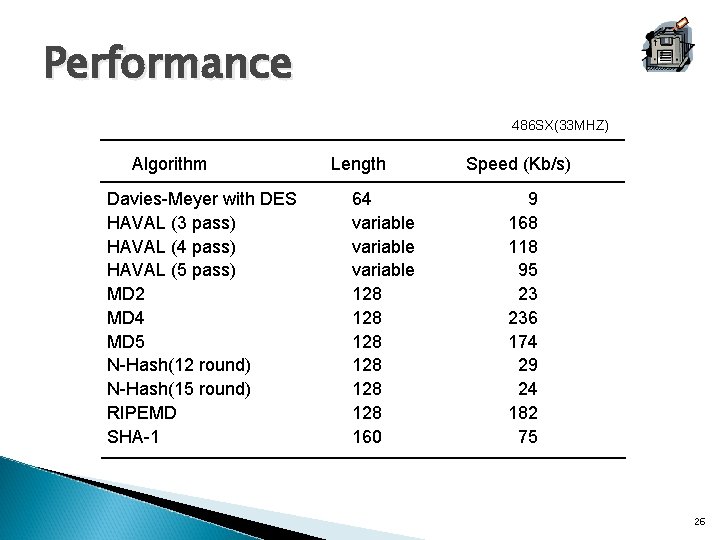
Performance 486 SX(33 MHZ) Algorithm Davies-Meyer with DES HAVAL (3 pass) HAVAL (4 pass) HAVAL (5 pass) MD 2 MD 4 MD 5 N-Hash(12 round) N-Hash(15 round) RIPEMD SHA-1 Length 64 variable 128 128 128 160 Speed (Kb/s) 9 168 118 95 23 236 174 29 24 182 75 26

HMAC Nested MAC algorithm from the composition of two (keyed) hash family The Keyed-Hash Message Authentication Code (HMAC), FIPS Pub 198, 2002 HMACk(x) = SHA-1[(K opad) || SHA-1((K ipad) || x)] where ipad = 3636 …. 36, opad = 5 C 5 C … 5 C K : 512 bit key x: message to be authenticated Secure against unknown-key collusion attack 27

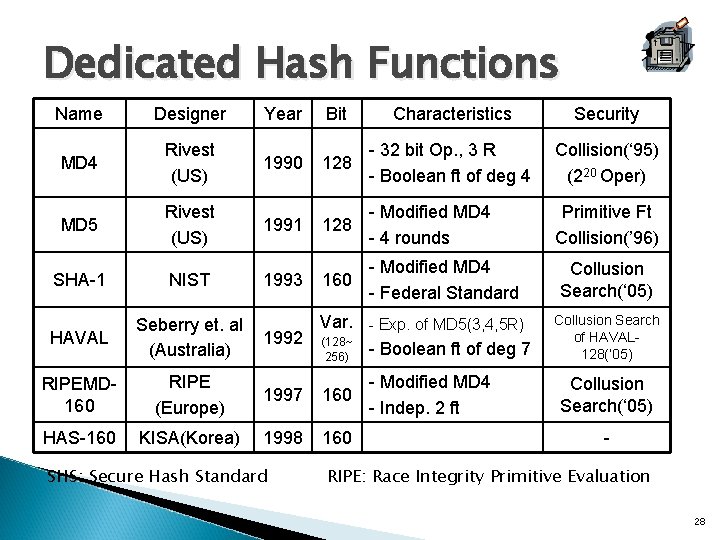
Dedicated Hash Functions Name Designer Year Bit Characteristics Security MD 4 Rivest (US) 1990 128 - 32 bit Op. , 3 R - Boolean ft of deg 4 Collision(‘ 95) (220 Oper) MD 5 Rivest (US) 1991 128 - Modified MD 4 - 4 rounds Primitive Ft Collision(’ 96) SHA-1 NIST 1993 160 - Modified MD 4 - Federal Standard HAVAL Seberry et. al (Australia) RIPEMD 160 RIPE (Europe) 1997 160 HAS-160 KISA(Korea) 1998 160 Var. - Exp. of MD 5(3, 4, 5 R) 1992 (128~ - Boolean ft of deg 7 256) SHS: Secure Hash Standard - Modified MD 4 - Indep. 2 ft Collusion Search(‘ 05) Collusion Search of HAVAL 128(‘ 05) Collusion Search(‘ 05) - RIPE: Race Integrity Primitive Evaluation 28

Collusion Search Attack 29

Previous Work on SHA-0/1 Chaubaud and Joux [Cr 98] ◦ SHA-0, 261, local collision and disturbance vector Biham and Chen [Cr 04] ◦ Near collision attack on SHA-0, 240 Biham, Joux and Chen [Cr 04 rump, EC 05] ◦ First real collision on SHA-0 (4 message blocks) found ◦ Collision attack on SHA-1 reduces to 50+ steps Rijmen and Osward [RSA-CT 05] ◦ Collision attack on SHA-1 reduces to 53 steps. 30

Publications X. Wang, Y. L. Yin and H. Yu, “Finding Collusions in the Full SHA-1”, Proc. of Crypto 2005, pp. 17 -36, LNCS 3621 X. Wang, H. Yu and Y. L. Yin, “Efficient Collusions Search Attacks on SHA-0”, Proc. of Crypto 2005, pp. 1 -16, LNCS 3621 X. Y. Wang, D. G. Feng, X. J. Lai and H. B. Yu, “Collusions for hash Functions MD 4, MD 5, HAVAL-128 and RIPEND”, IACR eprint, 2004/199 and Crypto 2005 Rump Session 31

Flow of Collusion Search 1. Find disturbance vector with low Hamming weights (difference for subtractions mod 232) 2. Construct differential paths by specifying conditions so that the differential path will occur with high probabilities. 3. Generate a message randomly, modify it using message modification techniques, and find a collusion 32

Summary Complexity of best known attack of MD 4 : 26, MD 5 : 233, SHA-0: 239, SHA-1: 269 More complex message preprocessing can provide more security ◦ But SHA-1, message expansion does not seem to have enough avalanche effect ◦ All step functions have unexpected weakness ◦ Addition and Boolean function can faciliate the attack More analysis is needed for SHA-256, -384, -512 which was defined in Secure Hash Standard (SHS), FIPS 1802, 2002, Aug 33

Example Message collusion of 58 steps SHA-1 34

SHA-3 Project 35