Harnessing Refraction Lenses A simple slab of glass

Harnessing Refraction: Lenses A simple slab of glass or other refractive material will transmit a ray of light (air-to-glass-to-air) with just a slight displacement—but with no “bending” of the ray from start to finish. That is, the first angle of incidence is equal to the final angle of refraction. With any shape other than a slab (i. e. other than two parallel surfaces for the ray to enter and exit), the above is not true. We use this fact and build various combinations of non-parallel surfaces— lenses—in order to bend light in useful ways: 2/8/19 OSU PH 212, Before Class #15 1

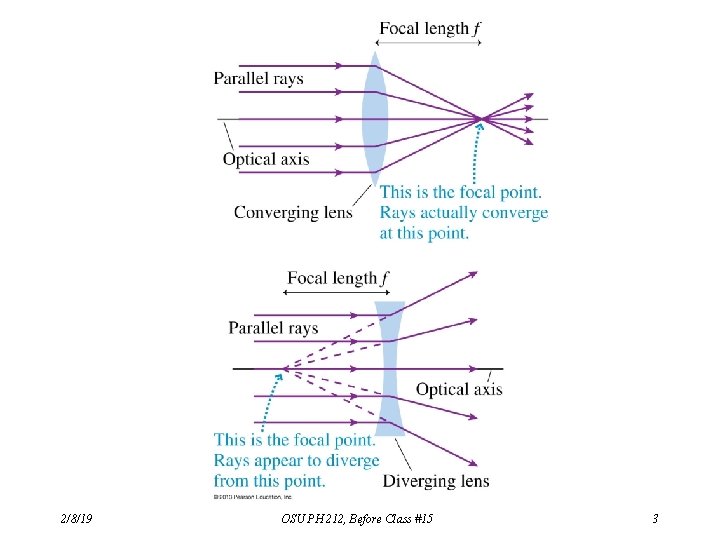
Converging vs. Diverging Lenses Converging lens: Incident parallel rays converge at a focal point on the refractive (right) side. If designed to be used in air (or any medium whose n value is less than that of the lens material), a converging lens is thicker in the center than at the edges. Diverging lens: Incident parallel rays diverge, so they appear to originate at a focal point on the incident (left) side. If designed to be used in air (or any medium whose n value is less than that of the lens material), a diverging lens is thinner in the center than at the edges. The focal length is the distance from the lens to the focal point, as measured along the central axis. 2/8/19 OSU PH 212, Before Class #15 2

2/8/19 OSU PH 212, Before Class #15 3

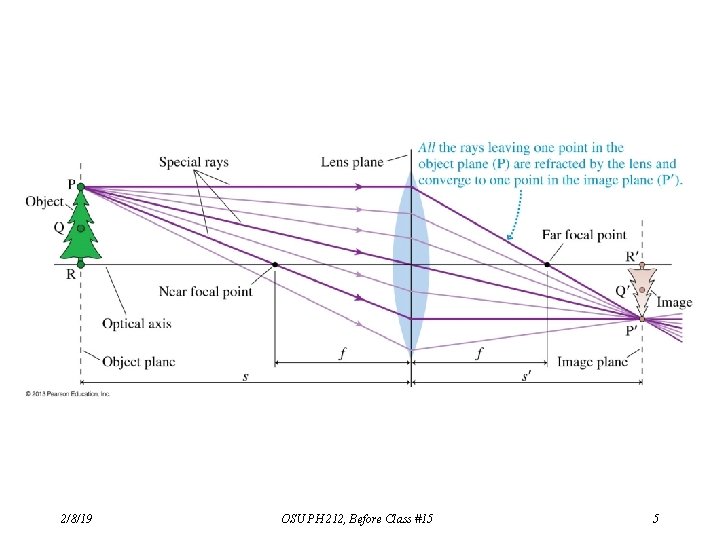
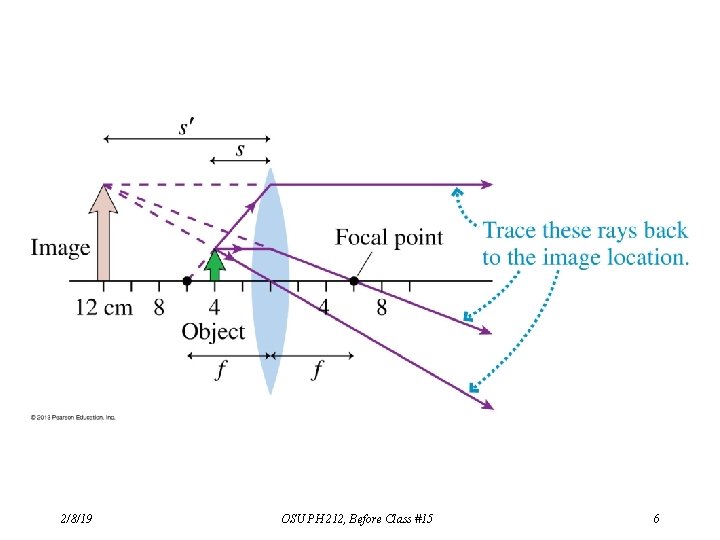
Ray Tracing with Thin Lenses To see how a lens determines an image location, size and orientation (compared to the object), one easy way is to trace a few rays to see how their lines converge at the image location. Three such rays are especially useful: (1) From the object to the lens along a path parallel to the lens’s principal axis, then refracting to align with the focal point, F*. (2) From the object toward the focal point, F*, then refracting out parallel to the principal axis. (3) From the object, straight through the center of the thin lens. *For a converging lens, use the focal point on the left (incident) side; for a diverging lens, use the focal point on the right side. 2/8/19 OSU PH 212, Before Class #15 4

2/8/19 OSU PH 212, Before Class #15 5

2/8/19 OSU PH 212, Before Class #15 6

2/8/19 OSU PH 212, Before Class #15 7

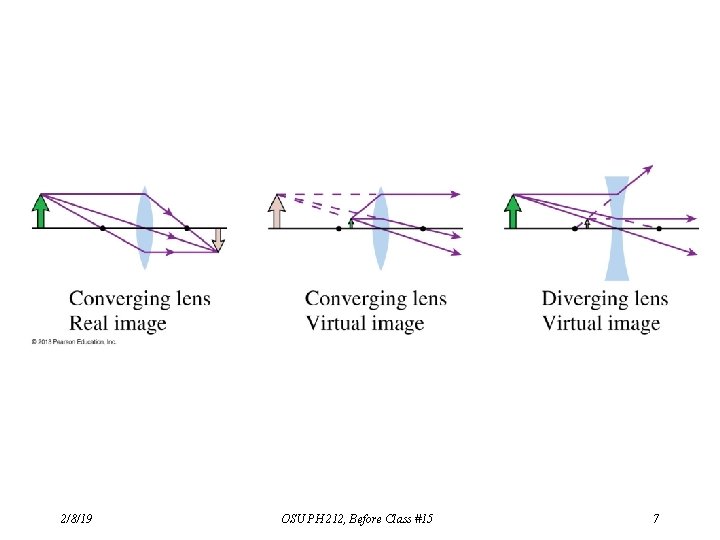
Formation of image with a Converging Lens summary: • If object is located outside of focal point (do > f ): - Image is inverted. - Image is real. - Image is enlarged if f < do < 2 f. - Image is reduced if do > 2 f. - Image is on opposite side of lens from object. - Examples: camera, eye, projector. • If object is located inside of focal point (do < f ): - Image is upright. - Image is virtual. - Image is enlarged. - Image is on same side of lens as object. - Example: magnifying glass. 2/8/19 OSU PH 212, Before Class #15 8

Formation of image with a Diverging Lens summary: - Image is upright. - Image is virtual. - Image is reduced in size. - Image is on same side of lens as object. 2/8/19 OSU PH 212, Before Class #15 9

The Thin-Lens Equation The thin lens approximation holds for a lens whose thickness is small compared to its focal length. With that assumption, plus some geometry and algebra, we can use this calculation for lenses: 1/d 0 + 1/di = 1/f Definitions and sign conventions: Object distance (d 0): + when object is left of the lens (real); Image distance (di): + if the image is right of the lens (real); – if the image is left of the lens (virtual). Focal length (f): + for a converging lens. – for a diverging lens. 2/8/19 OSU PH 212, Before Class #15 10

The Magnification Equation for Lenses The magnification equation for lenses is: m = hi/ho = –di/do where ho is the object height and hi is the image height (negative if the image is inverted with respect to the positive object height). The meaning of the sign of m: Assuming the object is upright: m is + if the image is upright. m is – if the image is inverted. 2/8/19 OSU PH 212, Before Class #15 11

1/do + 1/di = 1/f m = hi/ho = –di/do Practice: A lens has a focal length of – 32 cm. An object is placed 19 cm in front of it (to its left). • Calculate the image distance and magnification. • Describe the image. (Real/virtual? Upright/inverted? Enlarged/reduced? ) 2/8/19 OSU PH 212, Before Class #15 12

1/do + 1/di = 1/f m = hi/ho = –di/do Practice: A lens has a focal length of – 32 cm. An object is placed 19 cm in front of it (to its left). • • Calculate the image distance and magnification. Describe the image. (Real/virtual? Upright/inverted? Enlarged/reduced? ) do = 19, and f = – 32, so: 1/di = 1/f – 1/do Thus: di = (do)(f)/(do – f) = (19)(– 32)/(19 - – 32) = – 11. 9 cm The image distance is negative, so the image is virtual, upright and reduced—indeed, the only sort of image that a diverging lens (i. e. a lens with a negative f) can produce. Verify this with the magnification eqn. : m = –di/do = –(– 11. 9/19) = (+)0. 627 2/8/19 OSU PH 212, Before Class #15 13