Haringey Session 1 Supporting fluency and reasoning through

Haringey Session 1 Supporting fluency and reasoning through rich tasks 8 October 2014 Lynne Mc. Clure Director, NRICH project © University of Cambridge

National Curriculum Become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately. © University of Cambridge

National Curriculum Reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language © University of Cambridge

Reach 100 Choose four different digits from 1− 9 and put one in each box. For example: This gives four two-digit numbers: 52, 19, 51, 29 In this case their sum is 151. Can you find four different digits that give four two-digit numbers which add to a total of 100? © University of Cambridge

• What is the mathematical knowledge that is needed? • Who would this be for? • What is the ‘value added’ for higher attaining children/struggling children. 5 © University of Cambridge

Strike It Out 6 + 4 = 10 10 take away 9 makes 1 1 add 17 is 18 18…… Competitive aim – stop your partner from going Collaborative aim – cross off as many as possible 6 © University of Cambridge

• What is the mathematical knowledge that is needed to play? • Who would this game be for? • What is the ‘value added’ for able children/struggling children of playing the game? • How could you adapt this game to use it in your classroom? 7 © University of Cambridge

How do these rich tasks contribute to fluency? reasoning? © University of Cambridge

Efficiency An efficient strategy is one that the student can carry out easily, keeping track of subproblems and making use of intermediate results to solve the problem. © University of Cambridge

Efficiency Accuracy depends on careful recording, the knowledge of basic number combinations and other important number relationships, and checking results. © University of Cambridge

Efficiency Accuracy Flexibility requires the knowledge of more than one approach and being able to choose appropriately between them (Russell, 2000 http: //investigations. terc. edu/library/bookpapers/comp_fluency. cfm) © University of Cambridge

Procedural & conceptual fluency Automaticity with recall © University of Cambridge

Fluency Procedural without conceptual Conceptual without procedural Computation without meaning Computation which is slow, effortful and frustrating Inability to adapt skills to unfamiliar contexts Inability to focus on the bigger picture when solving problems Difficulty reconstructing forgotten knowledge or skills Difficulty progressing to new or more complex ideas © University of Cambridge

Using the same rules is it possible to cross all the numbers off? How do you know? 14 © University of Cambridge

Two types of reasoning Inductive reasoning • Can be incorrect • Can’t be used to ‘prove’ Deductive reasoning • Follows rules of logic • Can be used to prove © University of Cambridge

In a problem: • Reasoning is necessary when: • The route through the problem is not clear • There are some conflicts in what you are given or know • There are some things you don’t know • Theres no structure to what you’re given • There are different possible solutions • All of which require mental work…. © University of Cambridge

Reasoning is… • A critical skill to knowing and doing maths • Enabling – it allows children to make use of all the other mathematical skills – it’s the glue that helps maths to make sense. © University of Cambridge

Structuring children’s reasoning Questioning: closed v open Listening Acknowledging Improving Modelling KS 1: good 'because' statements, short chains • KS 2: logic, convincing • • • © University of Cambridge

Session 2 Problem solving © University of Cambridge

National Curriculum Can solve problems by applying their mathematics to a variety of routine and nonroutine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions © University of Cambridge

Historically • learning the content v problem solving • theory versus practice, reason versus experience, acquiring knowledge versus applying knowledge. • problems seen as vehicles for practicing applications ie computation procedures are acquired first and then applied • problem-based learning © University of Cambridge

Dominoes • • Dominoes – have a play…. Have you got a full set? How do you know? Can you arrange them in some way to convince yourself/others that you have/ haven’t got full set? © University of Cambridge

• What number knowledge/skills did you use? • What mathematical processes did you use? • What ‘soft skills’ did you use? © University of Cambridge

Amy has a box containing ordinary domino pieces but she does not think it is a complete set. She has 24 dominoes in her box and there are 125 spots on them altogether. Which of her domino pieces are missing? © University of Cambridge

• What number knowledge/skills did you use? • What mathematical processes did you use? • What ‘soft skills’ did you use? © University of Cambridge

Order of events • Free play –Montessori ‘work’ • Closed activity: structure of the apparatus • Task which uses that knowledge • Multistep • With or without apparatus Ruthven’s Ø Exploration Ø Codification Ø Consolidation © University of Cambridge

Dominoes v houses Sort – have you got them all? How do you know? Tasks using that knowledge Guess the dominoes/ houses © University of Cambridge

Rich tasks…. • combine fluency, problem solving and mathematical reasoning • are accessible • promote success through supporting thinking at different levels of challenge (low threshold - high ceiling tasks) • encourage collaboration and discussion • use intriguing contexts or intriguing maths © University of Cambridge

• allow for: • • learners to pose their own problems, different methods and different responses identification of elegant or efficient solutions, creativity and imaginative application of knowledge. • have the potential for revealing patterns or lead to generalisations or unexpected results, • have the potential to reveal underlying principles or make connections between areas of mathematics (adapted from Jenny Piggott, NRICH) © University of Cambridge

Tasks • • • Non-routine Accessible Challenging Curriculum linked Rich tasks/LTHC tasks Implications for your teaching? © University of Cambridge

Valuing mathematical thinking • • Process as well as end product Talk as well as recording Questioning as well as answering ………… © University of Cambridge

Purposeful activity Give the pupils something to do, not something to learn; and if the doing is of such a nature as to demand thinking; learning naturally results. John Dewey © University of Cambridge

Session 4 Games are more than fillers © University of Cambridge

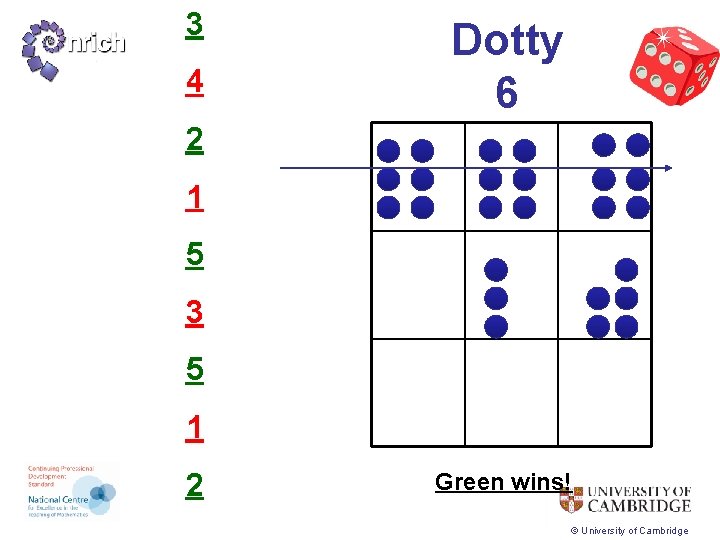
3 4 Dotty 6 2 1 5 3 5 1 2 Green wins! © University of Cambridge

• What is the mathematical knowledge that is needed to play? • Who would this game be for? • What is the value added of playing the game? • Could you adapt it to use it in your classroom? • Contribute to F, R, PS? © University of Cambridge

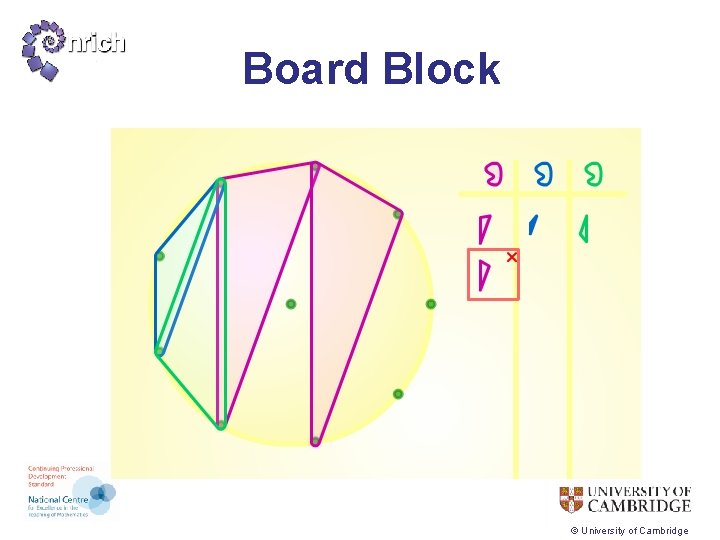
Board Block © University of Cambridge

• What is the mathematical knowledge that is needed to play? • Who would this game be for? • What is the value added of playing the game? • Could you adapt it to use it in your classroom? • Contribute to F, R, PS? © University of Cambridge

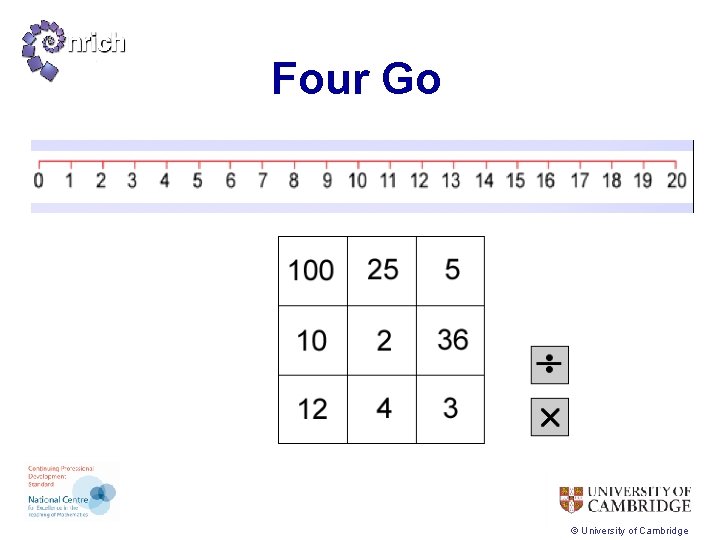
Four Go © University of Cambridge

• What is the mathematical knowledge that is needed to play? • Who would this game be for? • What is the value added of playing the game? • Could you adapt it to use it in your classroom? • Contribute to F, R, PS? © University of Cambridge

Nice and nasty © University of Cambridge

• What is the mathematical knowledge that is needed to play? • Who would this game be for? • What is the value added of playing the game? • Could you adapt it to use it in your classroom? • Contribute to F, R, PS? © University of Cambridge

© University of Cambridge

“If I ran a school, I’d give all the average grades to the ones who gave me all the right answers, for being good parrots. I’d give the top grades to those who made lots of mistakes and told me about them and then told me what they had learned from them. ” Buckminster Fuller, Inventor © University of Cambridge

• What were these children’s views of maths? • Would you get the same answers? © University of Cambridge

Session 3 Maths Working Group © University of Cambridge

Purpose of study Mathematics is a creative and highly interconnected discipline that has been developed over centuries, providing the solution to some of history’s most intriguing problems. It is essential to everyday life, critical to science, technology and engineering, and necessary for financial literacy and most forms of employment. A high-quality mathematics education therefore provides a foundation for understanding the world, the ability to reason mathematically, an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject. © University of Cambridge

Purpose of study Mathematics is a creative and highly interconnected discipline that has been developed over centuries, providing the solution to some of history’s most intriguing problems. It is essential to everyday life, critical to science, technology and engineering, and necessary for financial literacy and most forms of employment. A high-quality mathematics education therefore provides a foundation for understanding the world, the ability to reason mathematically, an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject. © University of Cambridge

• interconnected subject in which pupils need to be able to move fluently between representations of mathematical ideas. • make rich connections across mathematical ideas to develop fluency, mathematical reasoning and competence in solving increasingly sophisticated problems • apply their mathematical knowledge to science and other subjects. © University of Cambridge

• interconnected subject in which pupils need to be able to move fluently between representations of mathematical ideas. • make rich connections across mathematical ideas to develop fluency, mathematical reasoning and competence in solving increasingly sophisticated problems • apply their mathematical knowledge to science and other subjects. © University of Cambridge

The new National Curriculum What’s important to teachers? © University of Cambridge

Aims • All equally important • First two feed into third © University of Cambridge

• • • Big ideas Fluency Reasoning Problem solving Arithmetic/calculation (fractions) Multiplicative/proportional reasoning Pre-algebra/algebra Connections within and without No probability at KS 1/2 Reduced data handling at 1/2/3 © University of Cambridge

Year 6 Pupils should be taught to: • use simple formulae • generate and describe linear number sequences • express missing number problems algebraically • find pairs of numbers that satisfy an equation with two unknowns • enumerate all possibilities of combinations of two variables. • Pupils should be introduced to the use of symbols and letters to represent variables and unknowns in mathematical situations that they already understand, such as: • missing numbers, lengths, coordinates and angles, • formulae in mathematics and science • equivalent expressions (for example, a + b = b + a) • generalisations of number patterns • number puzzles (for example, what two numbers can add up to). © University of Cambridge

Year 6 Pupils should be taught to: • use simple formulae • generate and describe linear number sequences • express missing number problems algebraically • find pairs of numbers that satisfy an equation with two unknowns • enumerate all possibilities of combinations of two variables. • Pupils should be introduced to the use of symbols and letters to represent variables and unknowns in mathematical situations that they already understand, such as: • missing numbers, lengths, coordinates and angles, • formulae in mathematics and science • equivalent expressions (for example, a + b = b + a) • generalisations of number patterns • number puzzles (for example, what two numbers can add up to). © University of Cambridge

© University of Cambridge

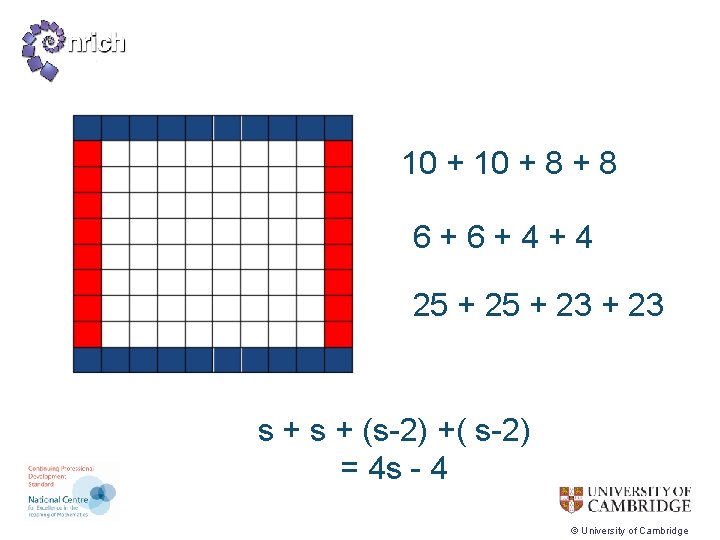
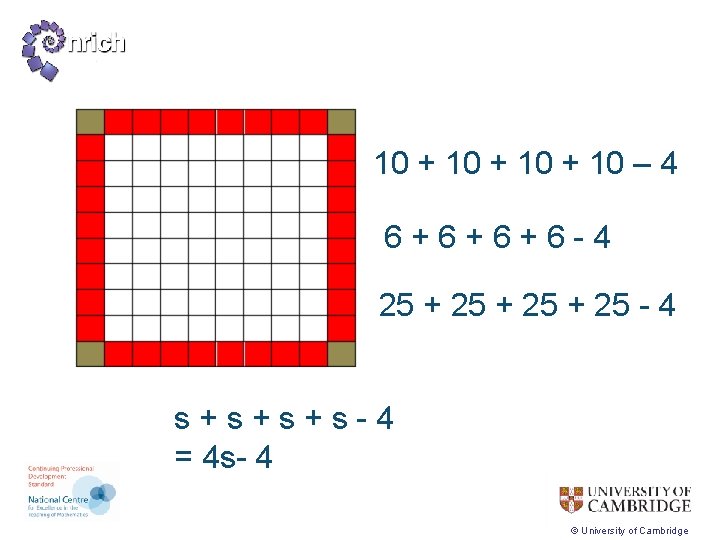
10 + 8 + 8 6+6+4+4 25 + 23 s + (s-2) +( s-2) = 4 s - 4 © University of Cambridge

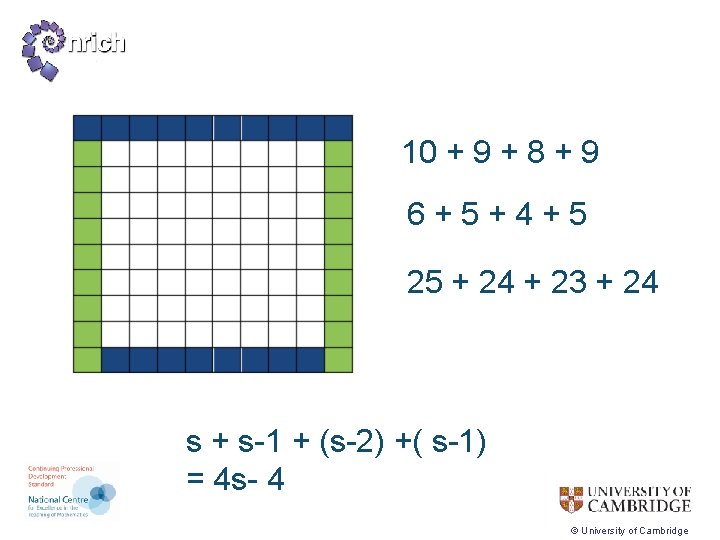
10 + 9 + 8 + 9 6+5+4+5 25 + 24 + 23 + 24 s + s-1 + (s-2) +( s-1) = 4 s- 4 © University of Cambridge

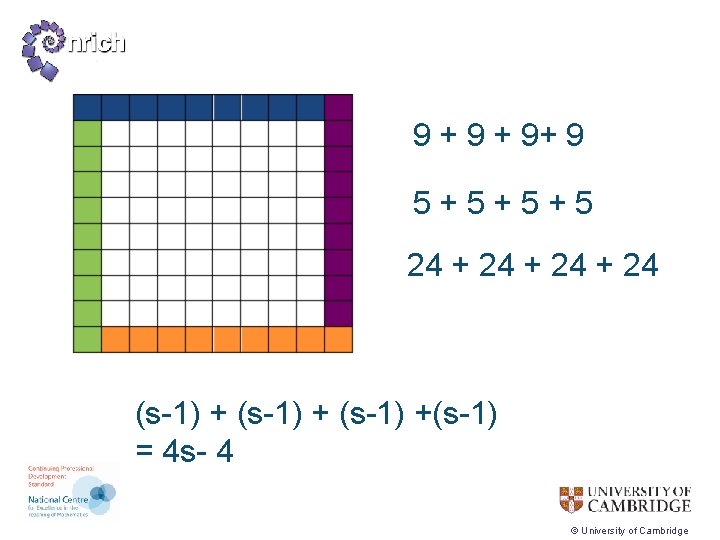
9 + 9+ 9 5+5+5+5 24 + 24 (s-1) +(s-1) = 4 s- 4 © University of Cambridge

10 + 10 – 4 6+6+6+6 -4 25 + 25 - 4 s+s+s+s-4 = 4 s- 4 © University of Cambridge

s + (s-2) +( s-2) = 4 s - 4 s + s-1 + (s-2) +( s-1) = 4 s- 4 (s-1) +( s-1) + (s-1) = 4 s- 4 s+s+s+s-4 = 4 s- 4 © University of Cambridge

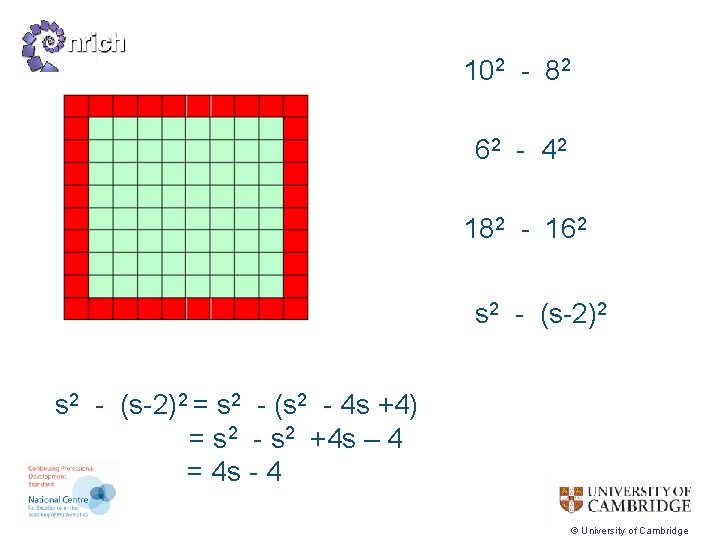
102 - 82 62 - 4 2 182 - 162 s 2 - (s-2)2 = s 2 - (s 2 - 4 s +4) = s 2 - s 2 +4 s – 4 = 4 s - 4 © University of Cambridge

The expectation is that the majority of pupils will move through the programmes of study at broadly the same pace. However, decisions about when to progress should always be based on the security of pupils’ understanding and their readiness to progress to the next stage. Pupils who grasp concepts rapidly should be challenged through being offered rich and sophisticated problems before any acceleration through new content. Those who are not sufficiently fluent with earlier material should consolidate their understanding, including through additional practice, before moving on. Opportunities? © University of Cambridge

The programmes of study for mathematics are set out year-by-year for Key Stages 1 and 2. Schools are, however, only required to teach the relevant programme of study by the end of the key stage. Within each key stage, schools therefore have the flexibility to introduce content earlier or later than set out in the programme of study. Opportunity? © University of Cambridge

IWADWADWAGWAG If we always do what we’ve always done we’ll always get what we always got…. . © University of Cambridge

Session 3 National Collaborative Projects a. Mastery pedagogy for primary mathematics 1 – China. England research and innovation project b. Mastery pedagogy for primary mathematics 2 – Use of high quality textbooks (linked to Singapore) to support teacher professional development and deep conceptual and procedural knowledge for pupils © University of Cambridge

1. Increasing supply of specialist teachers of mathematics (including primary, secondary convertors, Post-16) (SO 1 a) 2. Developing specialist subject knowledge of teachers of mathematics (all phases and including particular areas) (SO 1 b) 3. Developing pedagogical knowledge of teachers of mathematics (especially understanding of mastery pedagogy and Shanghai & Singapore pedagogy) (SO 1 c) 4. Improving quality of mathematics teaching practice (including the move from good to outstanding) (SO 1 d) 5. Supporting teachers to address new curriculum and qualifications © University of Cambridge

6. Improving quality of curriculum resources and activities (especially to support mastery teaching) (SO 3 b) 8. Improving supply and developing specialist leadership knowledge of mathematics subject leaders (SO 2 a/b) 9. Improving quality of and access to mathematics enrichment experiences (SO 3 c) 10. Increased progress and achievement in primary and secondary (including sustained progress through transition phases) (PO 1 a/b) 11. Reducing the gap in achievement between disadvantaged pupils and others (PO 4 c) 14. Developing confidence (can-do attitude) and resilience in learning mathematics (PO 3 a) © University of Cambridge

Key Findings Successful schools • • • Hands on crucial in FS and KS 1 ‘Traditional’ methods need to be underpinned by place value, mental methods fluency, facts Inverse operations important Confidence fluency and versatility nurtured through problem solving and investigations Clear coherent calculation policy © University of Cambridge

Key findings Made to Measure • • • Inconsistency within schools Need to increase emphasis on problem solving Teachers to be enabled to choose approaches that foster deeper understanding Checking understanding and reacting immediately Attention on most and least able © University of Cambridge