HardwareBased Implementations of Factoring Algorithms E Tromers presentation

Hardware-Based Implementations of Factoring Algorithms (E. Tromer’s presentation) Factoring Estimates for a 1024 -Bit RSA Modulus A. Lenstra, E. Tromer, A. Shamir, W. Kortsmit, B. Dodson, J. Hughes, and P. Leyland Springer On-line, Lecture Notes in CS 2894, pp. 55 -74 (2003) 1

Bicycle chain sieve [D. H. Lehmer, 1928] 2

The Quadratic Sieve How to find Ssuch that is a square? Look at the factorization of f 1(a): f 1(0)=10 2 f 1(1)=33 = 2 3 = 3 f 1(2)=14 95 f 1(3)=84 = 22 f 1(4)=61 6 M f 1(5)=14 5 f 1(6)=42 17 11 5 = 3 7 11 5 = = 2 3 32 23 7 = 23 24 13 29 7 50 72 112 This is a sq uare, becau se all expone nts are eve n. 3

Comparison: • Number Field Sieve (NFS): (1))·(log n)1/3·(log n)2/3 (α+o e • Quadratic Sieve (QS): (log n)^(1/2)*(log n)^(1/2) • L_a(n): Exp{ (c +o(1))* (log n)^a * (log n)^(1 -a)}, Then a = 0 polynomial, a=1 exponential. 4

The Sieving Problem Input: a set of arithmetic progressions. Each progression has a prime interval p and value logp. Output: indices where the sum of values exceeds a threshold. O O O O O O O O 5

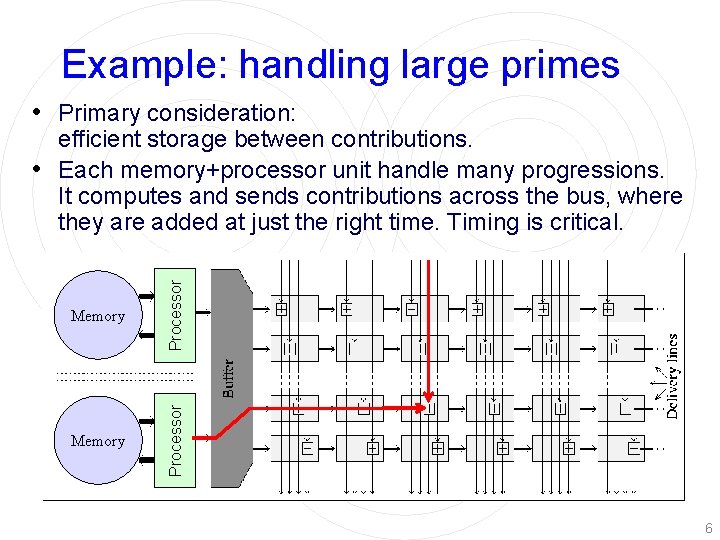
Example: handling large primes • Primary consideration: Memory Processor efficient storage between contributions. • Each memory+processor unit handle many progressions. It computes and sends contributions across the bus, where they are added at just the right time. Timing is critical. 6

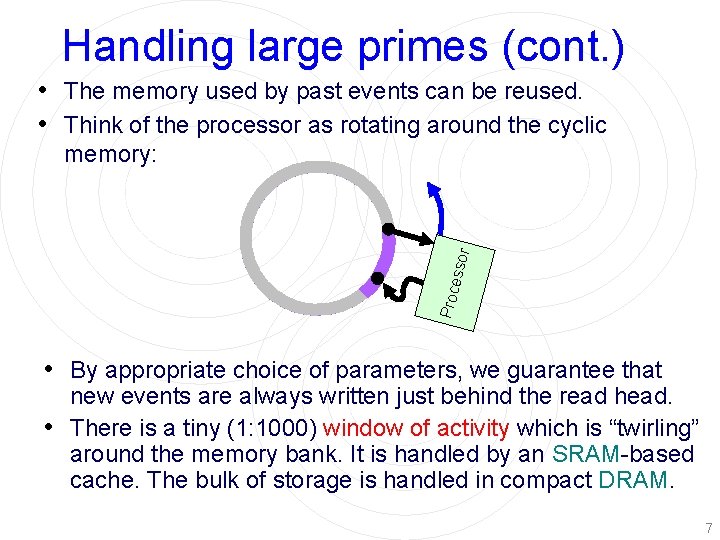
Handling large primes (cont. ) • The memory used by past events can be reused. • Think of the processor as rotating around the cyclic Proc esso r memory: • By appropriate choice of parameters, we guarantee that new events are always written just behind the read head. • There is a tiny (1: 1000) window of activity which is “twirling” around the memory bank. It is handled by an SRAM-based cache. The bulk of storage is handled in compact DRAM. 7

Rational vs. algebraic sieves • We actually have two sieves: rational and algebraic. We are looking for the indices that accumulated enough value in both sieves. • The algebraic sieve has many more progressions, and thus dominates cost. rational algebraic • We cannot compensate by making s much larger, since the pipeline becomes very wide and the device exceeds the capacity of a wafer. 8

Estimating NFS parameters • Predicting cost requires estimating the NFS parameters (smoothness bounds, sieving area, frequency of candidates etc. ). • Methodology: [Lenstra, Dodson, Hughes, Leyland] • Find good NFS polynomials for the RSA-1024 and RSA-768 composites. • Analyze and optimize relation yield for these polynomials according to smoothness probability functions. • Hope that cycle yield, as a function of relation yield, behaves similarly to past experiments. 9

1024 -bit NFS sieving parameters • Smoothness bounds: • Rational: • Algebraic: 3. 5£ 109 2. 6£ 1010 • Region: • a 2{-5. 5£ 1014, …, 5. 5£ 1014} • b 2{1, …, 2. 7£ 108} • Total: 3£ 1023 (£ 6/ 2) 10

TWIRL for 1024 -bit composites • A cluster of 9 TWIRLS R R R R can process a sieve line (1015 indices) in 34 seconds. A • To complete the sieving in 1 year, use 194 clusters. • Initial investment (NRE): ~$20 M • After NRE, total cost of sieving for a given 1024 -bit composite: ~10 M $ year (compared to ~1 T $ year). R 11

. 12