Hard problems in computer science Prof Noah Snavely

Hard problems in computer science Prof. Noah Snavely CS 1114 http: //www. cs. cornell. edu/courses/cs 1114/

Administrivia § Assignments: – A 6 due Friday § Prelim 3 next Thursday – Review in class Tuesday § Final project proposals – Most of you now have feedback – Demo session on Tuesday, May 15, 1: 30 -3: 30 2

Puzzle § Does this program terminate? i = 0; while true i = i + 1; end 3

Puzzle § How about this one? c = 2; while true for a = 2: c for b = 2: c if a^3 + b^3 == c^3 return; end end c = c + 1; end 4

Hard problems in computer science § Many problems in computer science are “polynomial time” problems – We know of an algorithm that solves the problem exactly in O(nk) time, for some constant k – Examples? § Many other problems have no known polynomial time algorithm – E. g. , problems whose fastest known algorithm takes O(2 n) time [exponential time] 5

Hard problems in computer science § Other problems cannot be solved at all in general – Given a program written in Matlab, does that program ever terminate? – A version of the halting problem – Vaguely related to the puzzle a moment ago 6

Exponential time algorithms § Many other problems have no known polynomial time algorithm – E. g. , algorithms whose best solution takes O(2 n) time § If it takes 1 second to solve such a problem with n = 100 § Then it takes 2 seconds to solve for n = 101 § And it takes 250 seconds to solve for n = 150 – About 3. 6 million years 7

Travelling Salesman Problem (TSP) § Classic hard problem in CS § Problem statement: – Given a weighted, complete graph with n nodes – Compute a tour that starts and ends at the same nodes, and visits all other nodes – Find such a tour that has the lowest total cost – A tour is also just a permutation of the nodes 8

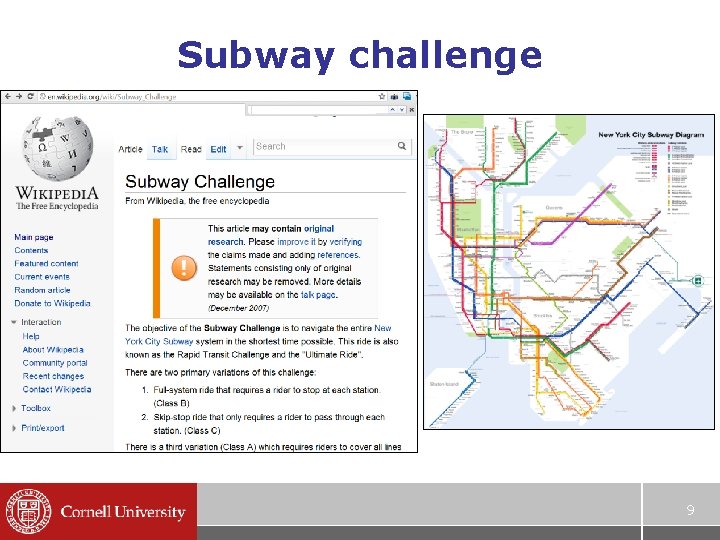
Subway challenge 9

Solving the TSP § What kind of algorithm might solve the TSP? § Can you come up with an example that breaks your algorithm? 10

Solving the TSP § What if the graph is metric? – Means that nodes could be laid out on the plane, with weights corresponding to distance in the plane § Easy to find a good approximation algorithm (on board) 11

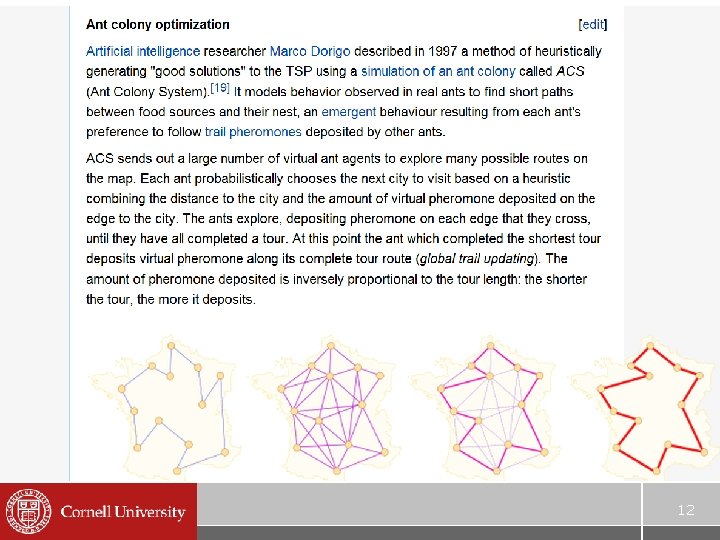
12

Other hard problems in CS § Hamiltonian cycle – Does a given graph contain a Hamiltonian cycle? – (Very related to TSP) § Graph coloring – Can a given graph be colored with k colors? 13

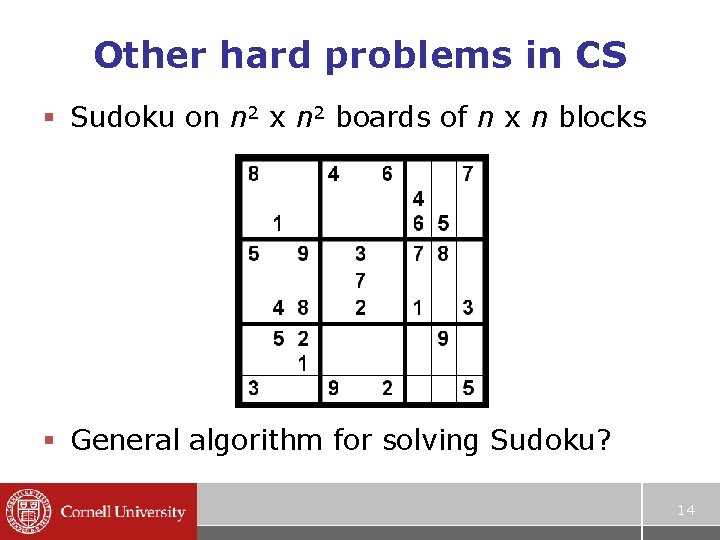
Other hard problems in CS § Sudoku on n 2 x n 2 boards of n x n blocks § General algorithm for solving Sudoku? 14