Haplotype Phasing using Semidefinite Programming Parag Namjoshi CSEE

Haplotype Phasing using Semidefinite Programming Parag Namjoshi CSEE Department University of Maryland Baltimore County Joint work with Konstantinos Kalpakis BIBE 05 1

Outline p p p Biology Review Motivation Previous work Our contribution Experimental results Conclusions BIBE 05 2

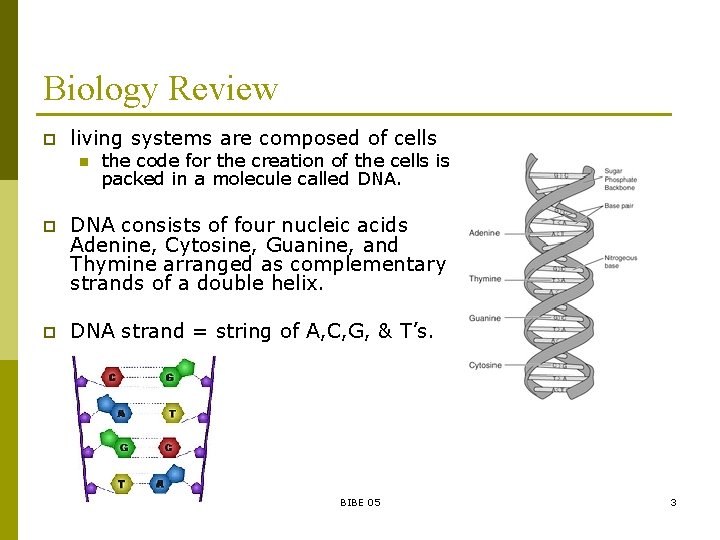
Biology Review p living systems are composed of cells n the code for the creation of the cells is packed in a molecule called DNA. p DNA consists of four nucleic acids Adenine, Cytosine, Guanine, and Thymine arranged as complementary strands of a double helix. p DNA strand = string of A, C, G, & T’s. BIBE 05 3

Chromosomes p the genome is arranged as set of distinct chromosomes. p mammals are diploids n n humans have 22 + x and y chromosomes occur in homologous pairs n one homologous chromosome is inherited from each parent n homologous chromosomes contain the same genes in the same order (up to mutations) BIBE 05 4

Single Nucleotide Polymorphisms. p p Single Nucleotide Polymorphism (SNP) = mutation of a single base. evidence suggests that in humans n n 90% of variation is due to SNPs DNA has long conserved regions punctuated by SNPs p n most SNPS are bi-allelic p p there is one SNP in approximately 1000 bases at any given locus, only two of the four possible nucleotides are present in 95% of the population the restriction (projection) of a DNA strand to SNP sites is a haplotype BIBE 05 5

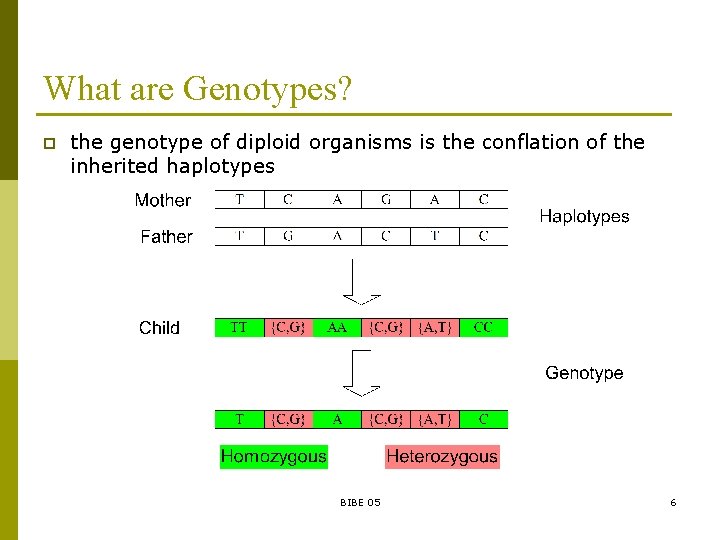
What are Genotypes? p the genotype of diploid organisms is the conflation of the inherited haplotypes BIBE 05 6

Genotype & Haplotype Std. Representation p genotypes and haplotypes can be represented as a 0, 1, 2 vectors n independently for each site p p p identify each one of the two letters that appear in it with 0 or 1 replace each homozygous site with 0/1 using the mapping above replace heterozygous sites with 2 BIBE 05 7

Haplotypes vs. Genotypes p p large scale polymorphism studies such as Linkage Disequilibrium need haplotype information however, experimentally n n p it is expensive to segregate the haplotypes of the individuals it is easier to observe the genotypes of those individuals can we find haplotypes from the genotypes computationally? n a genotype with h heterozygous sites can be explained (phased) by 2 h-1 different haplotype pairs n how do you choose among them? BIBE 05 8

Haplotype Phasing with Parsimony p in Population haplotyping, given genotypes from different individuals we want to find a set of haplotypes which resolve all the genotypes n n p HPP: Haplotype Phasing Problem with Pure Parsimony n p Given a set of genotypes, find a minimum size set of haplotypes which conflate to produce the given genotypes other criteria for choosing among possible sets of haplotypes are n p Recall that there can be many such solutions Experimental evidence suggests that the number of such haplotypes is small perfect phylogeny, minimum total pairwise distance, minimum diameter, etc we focus on HPP problem n Lancia, Pinotti, and Rizzi proved that the HPP is NP–complete as well as APX–hard BIBE 05 9

Clark’s Rule p Clark (1990) describes a greedy inference rule to find a small set of haplotypes resolving a set of genotypes n Starting with a set of haplotypes H that resolves all the homozygous genotypes, do the following p p p for each unresolved genotype g § if there is a pair (h, h’) that resolves g with h in H, then add h’ to H, else stop the solution obtained is sensitive to the order in which genotypes are resolved Clark’s rule may terminate with some genotypes unresolved (orphans) n The rule can be modified to include a pair of haplotypes that resolve an orphan genotype, and continue as before BIBE 05 10

Gusfield’s TIP p Gusfield (1999) introduces the TIP approach n n enumerate all distinct haplotypes that can be used to resolve any single heterozygous genotype solve an Integer linear Program (IP) to select a minimum size set haplotypes from the enumerated haplotypes that explains the genotypes TIP uses O(2 L n) variables and constraints, where L is the maximum number of heterozygous loci of any genotype Gusfield describes a number of important improvements to the basic approach above that improve performance BIBE 05 11

Harrower-Brown IP p Harrower and Brown give an alternate 0 -1 IP for the HPP problem (HB-IP) n n n explain the n genotypes with 2 n haplotypes (not necessarily distinct) the number of distinct haplotypes used are minimized the number of variables and constraints is polynomial in n, m BIBE 05 12

The QIP approach - Outline p p p arithmetic representation of genotypes semidefinite programming (SDP) Quadratic Integer Program (QIP) for HPP n p p a semidefinite programming based heuristic to solve QIP experimental results concluding remarks BIBE 05 13

Arithmetic Representation of Genotypes p represent each genotype g as a vector δ with n n p each homozygous locus takes value 0 or 2 iff it was 0 or 1 in g each heterozygous locus takes value 1 conflation can now be replaced by addition n if haplotypes h 1 and h 2 explain genotype δ, then p n δ = h 1 + h 2 we call δ an arithmetic genotype g=012 h 1= 0 1 0 δ = 021 g δ h 1= 0 1 0 h 2= 0 1 1 BIBE 05 14

Arithmetic Genotypes p p p let Δ be n x m matrix with the arithmetic genotypes as rows let H be k x m matrix with haplotypes as rows if haplotypes in H resolve Δ, then Δ=SH n where S is a n x k 0 -1 -2 matrix p p n the row of S for a homozygous genotype has a single 2 all other rows have exactly two 1 s we call S a selector matrix p ith row of S “selects” two haplotypes (rows of H) to explain genotype BIBE 05 15

The k-HPP Problem p the k-HPP problem n n Given nxm matrix Δ representing a set of n distinct genotypes each with m loci Find an nxk 0 -1 -2 selector matrix S and a kxm 0 -1 haplotype matrix H such that p p p Δ=SH S has as few non-zero columns as possible all row-sums of S are 2 p HPP is equivalent to k-HPP with k=2 n p lower Bounds for HPP n n is a well known lower bound Lemma: rank(Δ) is a lower bound for HPP p p Consider an optimal solution S, H Since Δ = S H, we know that rank(Δ) = min(rank(S), rank(H)), and thus H must have at least rank(Δ) distinct rows (haplotypes) BIBE 05 16

Finding H given Δ and S p given Δ and H to find an S is easy p given Δ and S find an H by solving a 2 -SAT problem n If genotype i is resolved by haplotypes t and l, then for each locus j, add following clauses p p p n If δi, j = 0, add two clauses (¬ht, j) ^ (¬hl, j) If δi, j = 2, add two clauses (ht, j) ^ (hl, j) If δi, j = 1, add clauses (ht, j V hl, j ) ^ (¬ht, j V ¬hl, j) § Only one of the ht, j , hl, j must both be 1 2 -SAT problem p p p has km variables and 2 nm clauses can be solved in (almost) linear time any satisfying assignment gives a resolution of the genotypes BIBE 05 17

Quadratic, Vector, and Semi-definite Programs p Quadratic Integer Program n n p Vector program n n p Optimize a quadratic objective function subject to quadratic constraints on integer variables Strict, when each term has total degree 0 or 2 optimize a linear objective function of inner products of vector variables subject to linear constraints on inner products of those variables Strict quadratic programs lead to vector programs (products of variables are mapped to inner products of corresponding vectors) SDP program n optimize a linear objective function of the elements of a matrix X subject to p p n p Vector programs lead to SDP (X is the matrix of all vector inner products) SDP programs can be solved in polynomial-time with small numerical errors, thus n n p linear constraints on the elements of X X being a positive semi-definite matrix solving vector programs, thus solving relaxations of strict Quadratic Integer programs construct an approximate solution to a quadratic integer program from a solution of its relaxation, obtained via SDP BIBE 05 18

Quadratic Integer Program for the k-HPP Subject to: BIBE 05 19

QIP Heuristic: SDP+Rounding+Backtracking p recursively solve k-HPP n n using SDP compute vectors for the variables of QIP for each selector variable Si, j, compute p n n n round to 1 the Si, j* with the highest P[Si, j] residual k-HPP=k-HPP problem with the rounded Si, j’s fixed to their rounded value if the residual k-HPP is infeasible p p n P[Si, j]=probability that a random hyperplane separates the vectors of Si, j and z variables (ala MAX-CUT) round Si, j* to 0 instead if the new residual k-HPP is still infeasible § backtrack by returning infeasible recursively solve the residual k-HPP BIBE 05 20

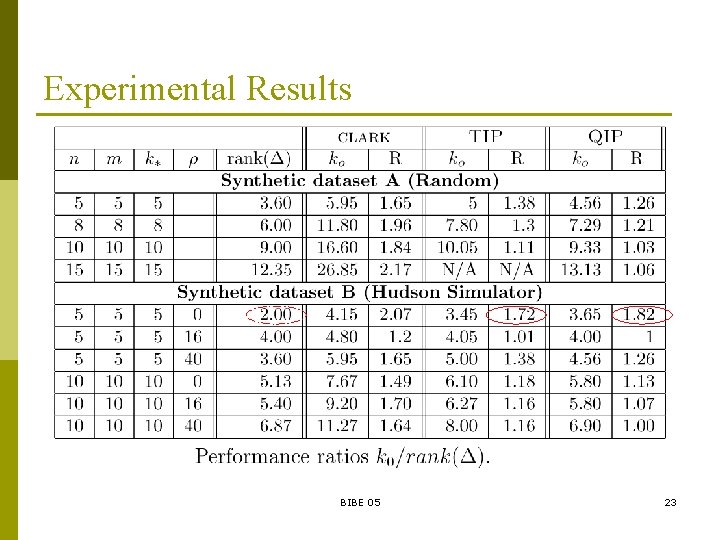
Experiments p we experiment with three approaches for the HPP problem n n n Clark’s rule LP relaxation of Gusfield’s TIP scheme with simple rounding the QIP heuristic for k–HPP with k = 2 n p p The MATLAB package SDPT 3. 02 is used to solve the SDP relaxation of the problem all experiments are done on a single CPU MATLAB on a Dual Xeon 2. 4 Ghz desktop with 1 GB memory BIBE 05 21

Experimental Datasets p we use synthetic datasets A and B n p generate instances of the HPP problem as follows n p randomly mate k haplotypes with m loci to produce n genotypes generation of haplotypes for dataset A n p each with 20 instances for each triplet (n, m, k) = (5, 5, 5), (8, 8, 8), (10, 10), and (15, 15) (and for B, recombination levels ρ = 0, 16 and 40) each locus of k haplotypes takes value 0/1 with probability ½ independent of other loci and other genotypes generation of haplotypes for dataset B n Use Hudson’s program to generate haplotypes with these parameters p p p diploid population of size 106 mutation rate = 1. 5 × 10 -6 recombination levels ρ = 0, 16 and 40 corresponding to crossover probabilities 0, 4 × 10 -6, and 10 -5 BIBE 05 22

Experimental Results BIBE 05 23

QIP Extensions p QIP can be extended to handle many variants of basic k-HPP problem, such as n partial Genotypes p n shared haplotypes p n n Some loci in some genotypes are unknown Prior knowledge of shared haplotypes allowing for erroneous genotypes and loci editing allowing for outlier genotypes BIBE 05 24

Concluding Remarks p developed arithmetic formulation for the HPP problem n n n p SDP relaxation of QIP that can be solved in polynomial time n p SDP+rounding+backtracking gives QIP heuristic experimentally n n p provides new lower bound yields simple quadratic IP (QIP) QIP can be extended to handle many variants, incorporate prior information etc Demonstrate competitiveness of QIP heuristic vs Clark’s rule and Gusfield’s TIP relaxation Show that rank of the genotypes is a tighter lower bound than future work n n Analysis of worst-case performance ratio of the QIP heuristic Devise algorithms that scale better BIBE 05 25

Thank You ! Questions ? BIBE 05 26