Hanyang University Antenna Theory By CONSTANTINE A BALANIS

Hanyang University Antenna Theory By CONSTANTINE A. BALANIS Ch 5. 4. 1~5. 7. 2 O Yeon Jeong 1/27

Hanyang University Contents 5. Loop Antennas 5. 4. 1 Arrays 5. 4. 2 Design procedure 5. 5 Ground and earth curvature effects for circular loops 5. 6 Polygonal loop antennas 5. 6. 1 Square loop 5. 6. 2 Triangular, Rectangular, and rhombic loops 5. 7 Ferrite loop 5. 7. 1 Radiation Resistance 5. 7. 2 Ferrite-loaded receiving loop 2/27

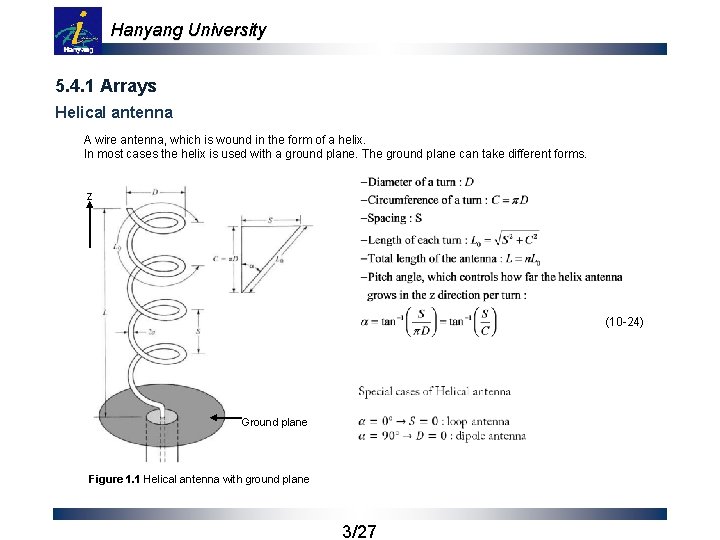
Hanyang University 5. 4. 1 Arrays Helical antenna A wire antenna, which is wound in the form of a helix. In most cases the helix is used with a ground plane. The ground plane can take different forms. z (10 -24) Ground plane Figure 1. 1 Helical antenna with ground plane 3/27

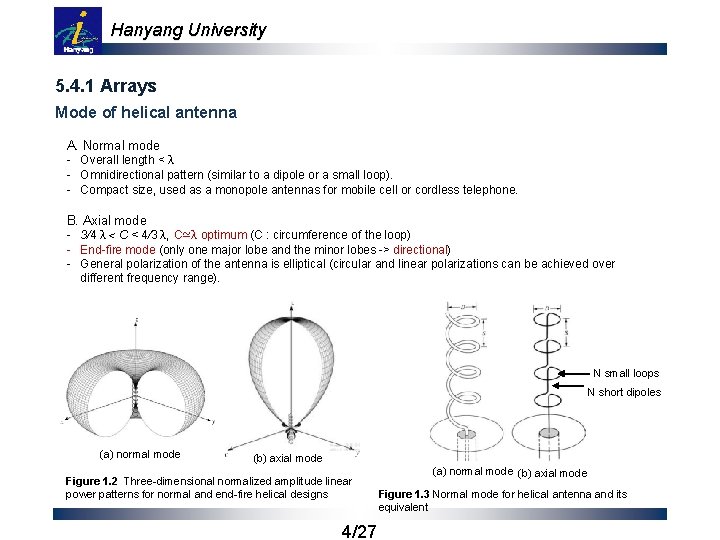
Hanyang University 5. 4. 1 Arrays Mode of helical antenna A. Normal mode - Overall length < λ - Omnidirectional pattern (similar to a dipole or a small loop). - Compact size, used as a monopole antennas for mobile cell or cordless telephone. B. Axial mode - 3/4 λ< C < 4/3 λ, C≃λ optimum (C : circumference of the loop) - End-fire mode (only one major lobe and the minor lobes -> directional) - General polarization of the antenna is elliptical (circular and linear polarizations can be achieved over different frequency range). N small loops N short dipoles (a) normal mode (b) axial mode Figure 1. 2 Three-dimensional normalized amplitude linear power patterns for normal and end-fire helical designs 4/27 (a) normal mode (b) axial mode Figure 1. 3 Normal mode for helical antenna and its equivalent

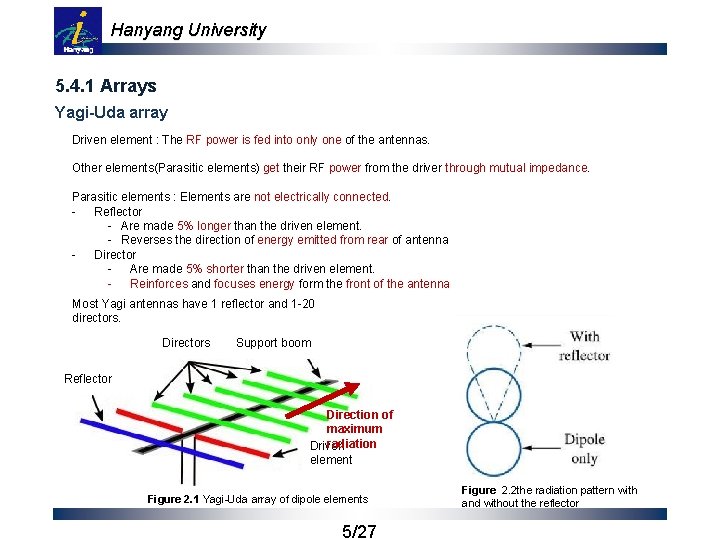
Hanyang University 5. 4. 1 Arrays Yagi-Uda array Driven element : The RF power is fed into only one of the antennas. Other elements(Parasitic elements) get their RF power from the driver through mutual impedance. Parasitic elements : Elements are not electrically connected. - Reflector - Are made 5% longer than the driven element. - Reverses the direction of energy emitted from rear of antenna - Director - Are made 5% shorter than the driven element. - Reinforces and focuses energy form the front of the antenna Most Yagi antennas have 1 reflector and 1 -20 directors. Directors Support boom Reflector Direction of maximum radiation Driven element Figure 2. 1 Yagi-Uda array of dipole elements 5/27 Figure 2. 2 the radiation pattern with and without the reflector

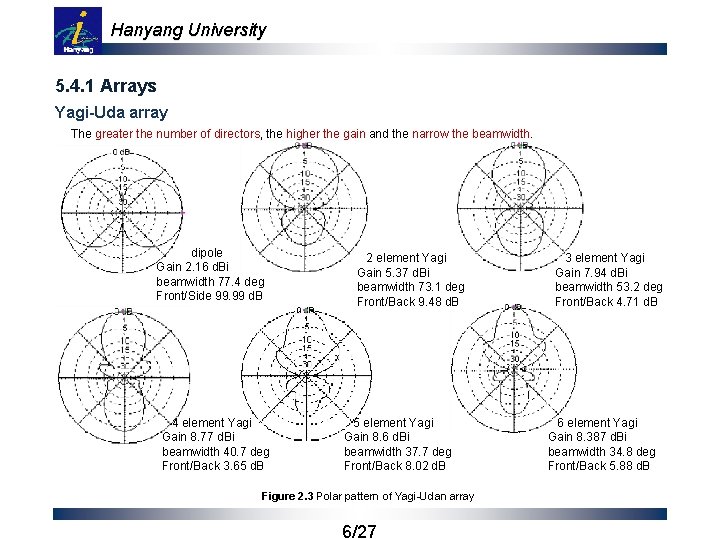
Hanyang University 5. 4. 1 Arrays Yagi-Uda array The greater the number of directors, the higher the gain and the narrow the beamwidth. dipole Gain 2. 16 d. Bi beamwidth 77. 4 deg Front/Side 99. 99 d. B 4 element Yagi Gain 8. 77 d. Bi beamwidth 40. 7 deg Front/Back 3. 65 d. B 2 element Yagi Gain 5. 37 d. Bi beamwidth 73. 1 deg Front/Back 9. 48 d. B 5 element Yagi Gain 8. 6 d. Bi beamwidth 37. 7 deg Front/Back 8. 02 d. B Figure 2. 3 Polar pattern of Yagi-Udan array 6/27 3 element Yagi Gain 7. 94 d. Bi beamwidth 53. 2 deg Front/Back 4. 71 d. B 6 element Yagi Gain 8. 387 d. Bi beamwidth 34. 8 deg Front/Back 5. 88 d. B

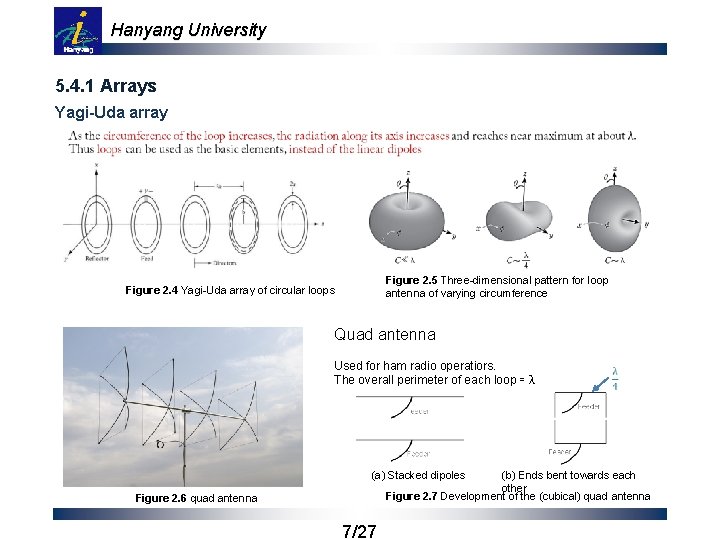
Hanyang University 5. 4. 1 Arrays Yagi-Uda array Figure 2. 5 Three-dimensional pattern for loop antenna of varying circumference Figure 2. 4 Yagi-Uda array of circular loops Quad antenna Used for ham radio operatiors. The overall perimeter of each loop ≃ λ (a) Stacked dipoles (b) Ends bent towards each other Figure 2. 7 Development of the (cubical) quad antenna Figure 2. 6 quad antenna 7/27

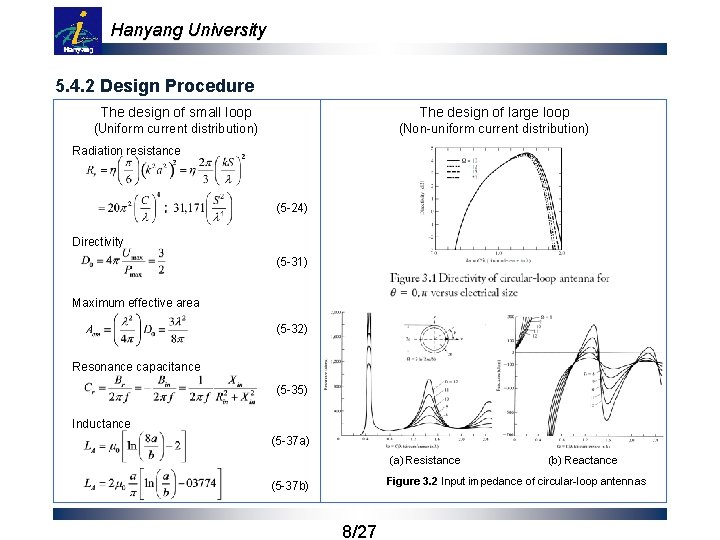
Hanyang University 5. 4. 2 Design Procedure The design of small loop The design of large loop (Uniform current distribution) (Non-uniform current distribution) Radiation resistance (5 -24) Directivity (5 -31) Maximum effective area (5 -32) Resonance capacitance (5 -35) Inductance (5 -37 a) (a) Resistance (b) Reactance Figure 3. 2 Input impedance of circular-loop antennas (5 -37 b) 8/27

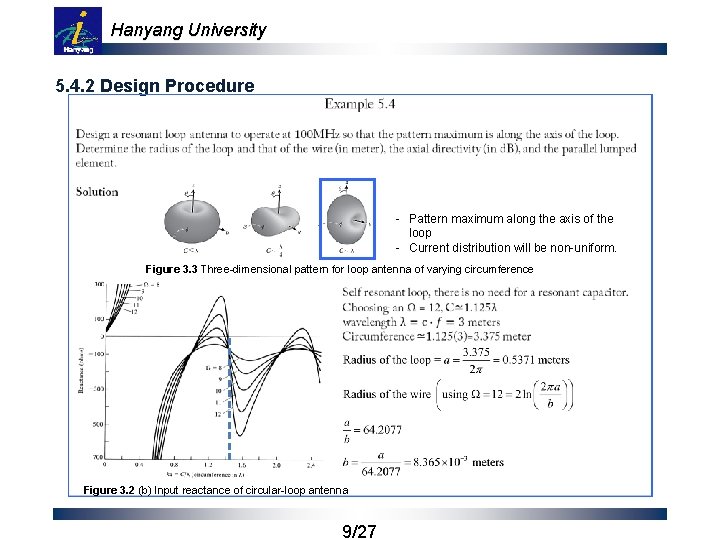
Hanyang University 5. 4. 2 Design Procedure - Pattern maximum along the axis of the loop - Current distribution will be non-uniform. Figure 3. 3 Three-dimensional pattern for loop antenna of varying circumference Figure 3. 2 (b) Input reactance of circular-loop antenna 9/27

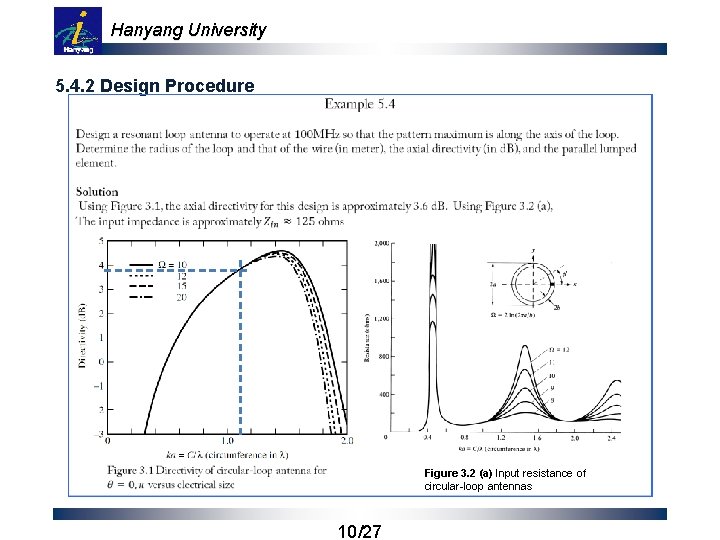
Hanyang University 5. 4. 2 Design Procedure Figure 3. 2 (a) Input resistance of circular-loop antennas 10/27

Hanyang University 5. 5 Ground and earth curvature effects for circular loops The reflections are taken into account by introducing appropriate image source. The effect of the ground curvature is taken into account by introducing divergence factor. Figure 4. 1 Vertical electric dipole above an infinite, flat, perfect electric conductor Figure 4. 2 Geometry for reflections from a spherical surface 11/27

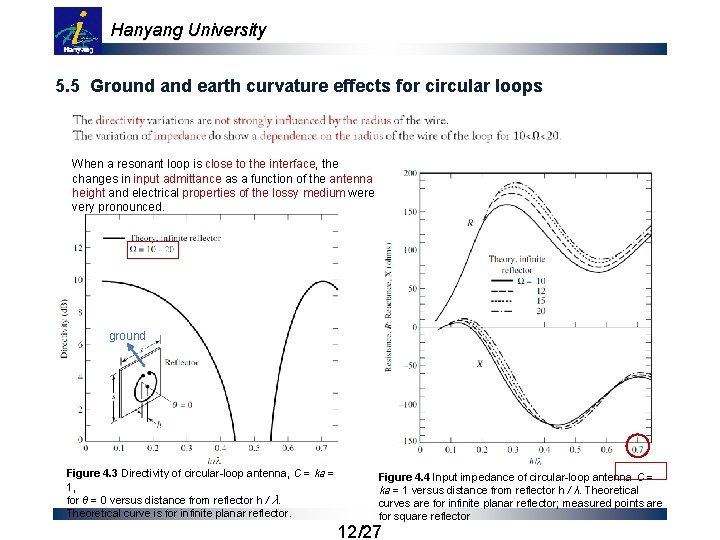
Hanyang University 5. 5 Ground and earth curvature effects for circular loops When a resonant loop is close to the interface, the changes in input admittance as a function of the antenna height and electrical properties of the lossy medium were very pronounced. ground Figure 4. 3 Directivity of circular-loop antenna, C = ka = 1, for θ = 0 versus distance from reflector h / λ. Theoretical curve is for infinite planar reflector. Figure 4. 4 Input impedance of circular-loop antenna C = ka = 1 versus distance from reflector h / λ. Theoretical curves are for infinite planar reflector; measured points are for square reflector 12/27

Hanyang University 5. 6 Polygonal loop antennas Usually, the circular loop has been used in the UHF range because of its high directivity while triangular and square loops have been applied in the HF and UHF bands because of advantages in their mechanical construction. Broadband impedance characteristics can be obtained from the different polygonal loops. Figure 5. 1 Triangular loop antenna Figure 5. 2 Rectangular loop antenna Figure 5. 3 Square loop antenna 13/27 Figure 5. 4 rhombic loop antenna

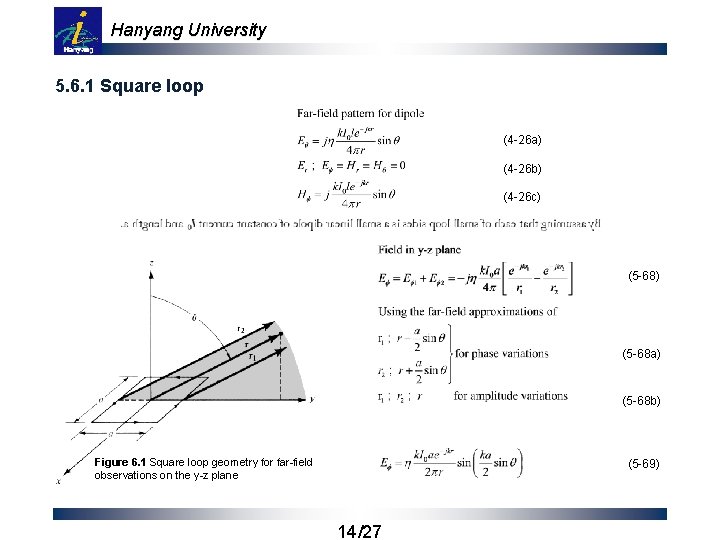
Hanyang University 5. 6. 1 Square loop (4 -26 a) (4 -26 b) (4 -26 c) (5 -68) (5 -68 a) (5 -68 b) Figure 6. 1 Square loop geometry for far-field observations on the y-z plane (5 -69) 14/27

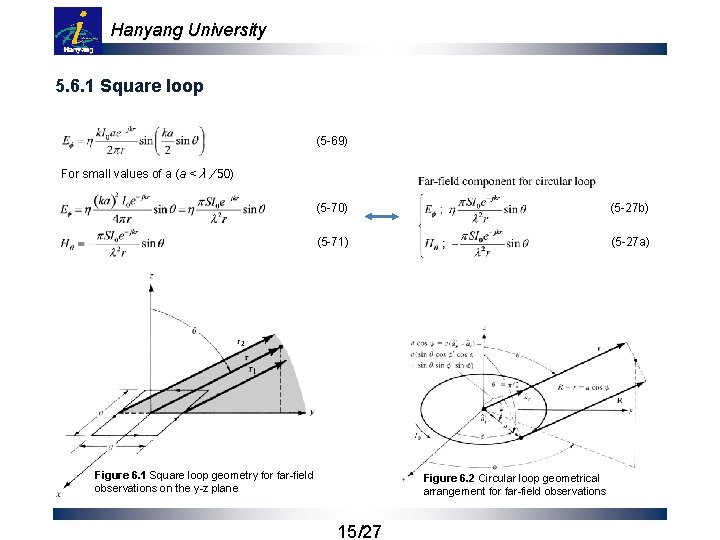
Hanyang University 5. 6. 1 Square loop (5 -69) For small values of a (a < λ / 50) (5 -70) (5 -27 b) (5 -71) (5 -27 a) Figure 6. 1 Square loop geometry for far-field observations on the y-z plane Figure 6. 2 Circular loop geometrical arrangement for far-field observations 15/27

Hanyang University 5. 6. 2 Triangular, rectangular, and rhombic loops Feed at the top corner of the isosceles triangle Feed at its terminals at the base Feed at its terminals at one of its corners Feed at the center of one of its side Figure 7. 3 Typical configurations of polygonal loop antennas 16/27

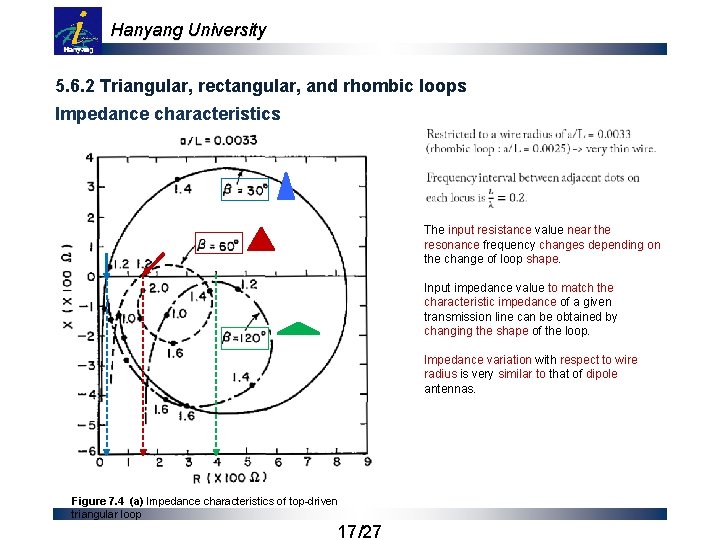
Hanyang University 5. 6. 2 Triangular, rectangular, and rhombic loops Impedance characteristics The input resistance value near the resonance frequency changes depending on the change of loop shape. Input impedance value to match the characteristic impedance of a given transmission line can be obtained by changing the shape of the loop. Impedance variation with respect to wire radius is very similar to that of dipole antennas. Figure 7. 4 (a) Impedance characteristics of top-driven triangular loop 17/27

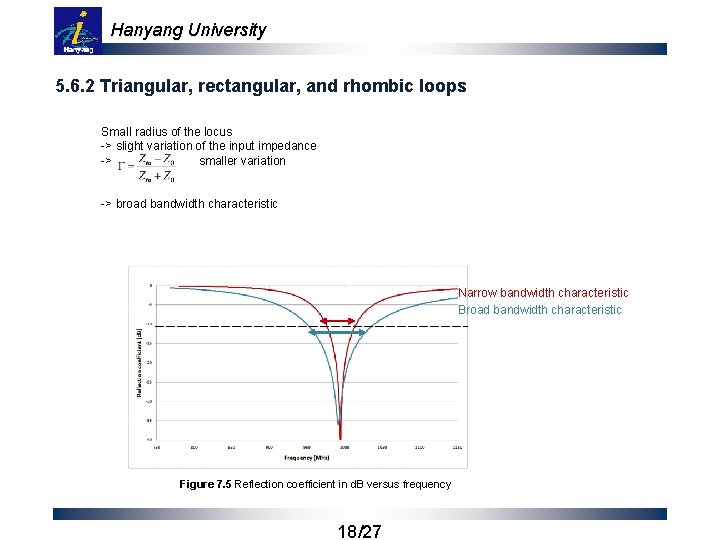
Hanyang University 5. 6. 2 Triangular, rectangular, and rhombic loops Small radius of the locus -> slight variation of the input impedance -> smaller variation -> broad bandwidth characteristic Narrow bandwidth characteristic Broad bandwidth characteristic Figure 7. 5 Reflection coefficient in d. B versus frequency 18/27

Hanyang University 5. 6. 2 Triangular, rectangular, and rhombic loops Impedance characteristics (a) (b) (d) (c) Figure 7. 4 Impedance characteristics (a) Top-driven triangular loop (b) Rectangular loop (c) Base-driven triangular loop (d) Rhombic loop 19/27

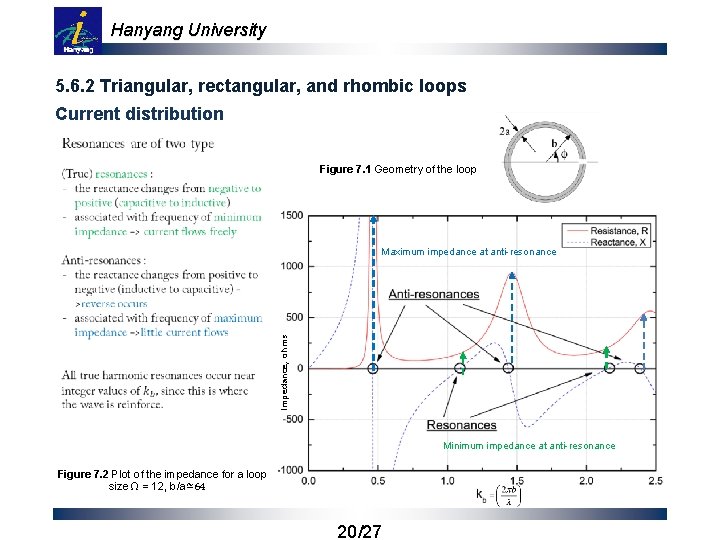
Hanyang University 5. 6. 2 Triangular, rectangular, and rhombic loops Current distribution Figure 7. 1 Geometry of the loop Impedance, ohms Maximum impedance at anti-resonance Minimum impedance at anti-resonance Figure 7. 2 Plot of the impedance for a loop size Ω = 12, b/a≃64 20/27

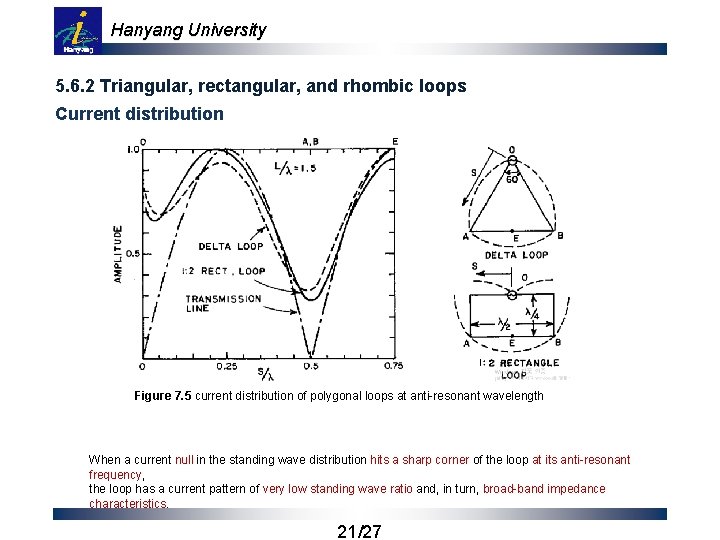
Hanyang University 5. 6. 2 Triangular, rectangular, and rhombic loops Current distribution Figure 7. 5 current distribution of polygonal loops at anti-resonant wavelength When a current null in the standing wave distribution hits a sharp corner of the loop at its anti-resonant frequency, the loop has a current pattern of very low standing wave ratio and, in turn, broad-band impedance characteristics. 21/27

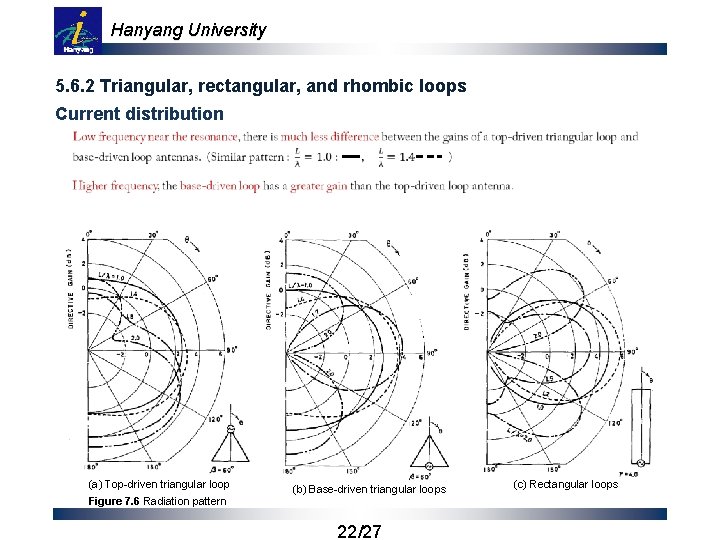
Hanyang University 5. 6. 2 Triangular, rectangular, and rhombic loops Current distribution (a) Top-driven triangular loop Figure 7. 6 Radiation pattern (b) Base-driven triangular loops 22/27 (c) Rectangular loops

Hanyang University 5. 7 Ferrite loop The radiation resistance of loop antenna is comparable with its loss resistance. Therefore, the radiation efficiency of loop antenna is quite low. To improve, radiation efficiency of a loop antenna, - Increasing the circumference of loop - Employing ferrite rods Figure 8. 1 Radiation resistance for a constant current circular-loop antenna Figure 8. 2 ferrite rod antenna 23/27

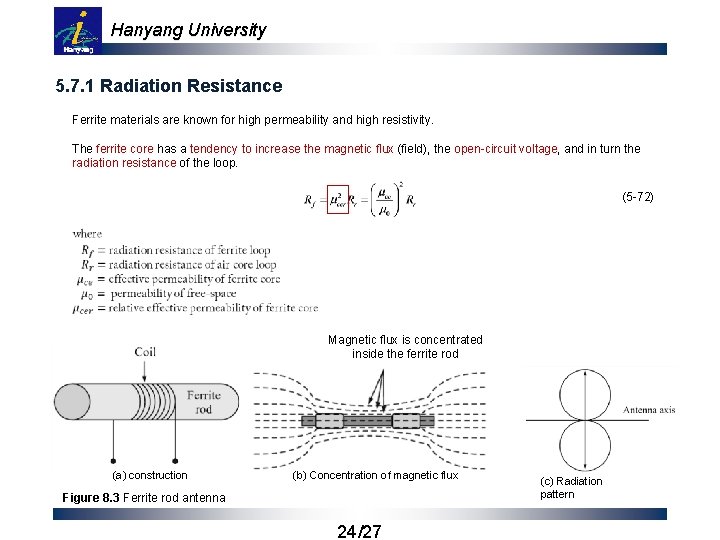
Hanyang University 5. 7. 1 Radiation Resistance Ferrite materials are known for high permeability and high resistivity. The ferrite core has a tendency to increase the magnetic flux (field), the open-circuit voltage, and in turn the radiation resistance of the loop. (5 -72) Magnetic flux is concentrated inside the ferrite rod (a) construction (b) Concentration of magnetic flux Figure 8. 3 Ferrite rod antenna 24/27 (c) Radiation pattern

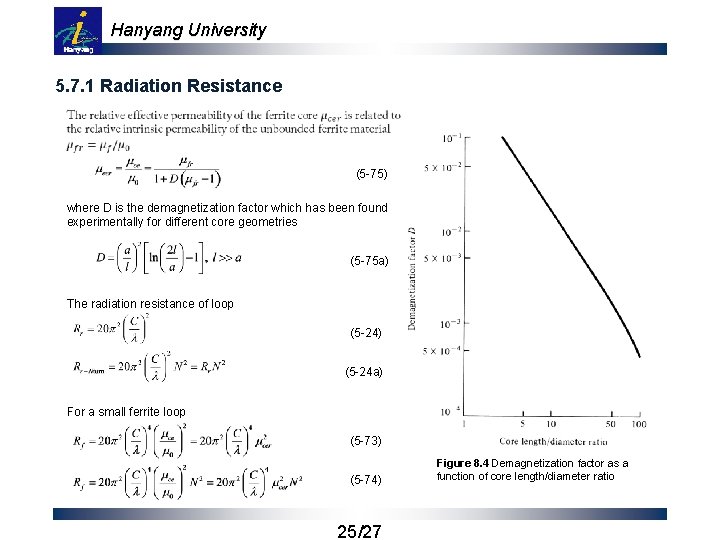
Hanyang University 5. 7. 1 Radiation Resistance (5 -75) where D is the demagnetization factor which has been found experimentally for different core geometries (5 -75 a) The radiation resistance of loop (5 -24) (5 -24 a) For a small ferrite loop (5 -73) (5 -74) 25/27 Figure 8. 4 Demagnetization factor as a function of core length/diameter ratio

Hanyang University 5. 7. 2 Ferrite-loaded receiving loop The combination of a low resistance with a large inductance can make it difficult to match the antenna as a source or load. To deal with this problem, a capacitor is used to turn the loop into a resonant circuit / antenna. Figure 8. 5 (a) Tuned ferrite rod antenna equivalent circuit Figure 8. 5 (b) Tuned ferrite rod antenna equivalent circuit Resonant frequency Quality factor 26/27

Hanyang University Thank you for attention. 27/27