Hamming Code Examples This is VERY tricky to

Hamming Code Examples This is VERY tricky to get you head around BUT simple once you know what’s happening!!!

Assumptions • You know what an even parity bit check is • You know what binary is • You know that a binary “word” could represent almost anything • Original ASCII comprises of 7 -bits • You have read the intro to hamming on page 113 of Bond & Langfield

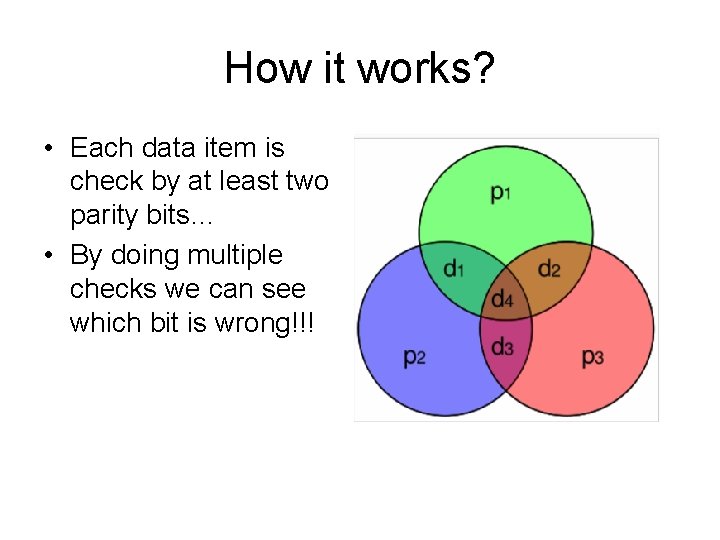
How it works? • Each data item is check by at least two parity bits… • By doing multiple checks we can see which bit is wrong!!!

Using Hamming Code Checks • • Lets start with 4 bits of Data This would require 3 parity bits (7 bits total) Parity bits are placed in positions 2 n Hamming Checks – – Start at n Check n Skip n E. g. Parity bit 2 is in position 2 so… Start at 2, check two positions, skip two positions, etc. . 2, 3, 6, 7 are part of the pattern that P 2 checks Position n 7 6 5 4 3 2 1 What’s There Data Bit 4 Data Bit 3 Data Bit 2 Parity Bit 3 (P 3) Data Bit 1 Parity Bit 2 (P 2) Parity Bit 1 (P 1)

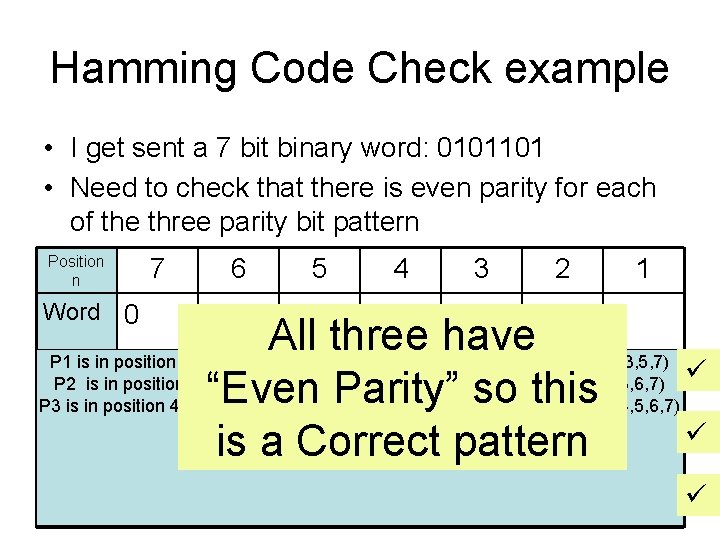
Hamming Code Check example • I get sent a 7 bit binary word: 0101101 • Need to check that there is even parity for each of the three parity bit pattern Position n 7 6 5 4 Word 0 1 P 3 1 0 1 3 1 2 0 1 1 All three have P 1 is in position 1 so… Start at 1, check 1, skip 1, check 1 skip 1 etc. . (1, 3, 5, 7) P 1 0 1 P 2 is in position 2 so… Start 0 at 2 check 2, skip 2 1 check 2 skip 2 rtc. . (2, 3, 6, 7) “Even Parity” so this P 3 is in position 4 so…Start at 4, check 4 skip 4(then we run out of bits) (4, 5, 6, 7) P 2 0 1 0 is a Correct 1 pattern 0

Hamming Code Check example 2 • I get sent a 7 bit binary word: 0001101 • Need to check that there is even parity for each of the three parity bit pattern Position 7 6 5 4 3 2 1 n P 20 and 0 P 31 don’t 1 have 0 1 Parity” this is 1 P 1 0 “Even 01, check 1, skipso P 1 is in position 1 so… Start at 1, 1 check 1 skip 1 etc. . (1, 3, 5, 7) P 2 is in position 2 so… Start at 2 check 2, skip 2 check 2 skip 2 rtc. . (2, 3, 6, 7) NOT P 3 is in position 4 so…Starta at 4, correct check 4 skip 4(thenpattern we run out of bits) (4, 5, 6, 7) P 2 0 0 1 0 Word 0 x P 3 0 0 0 1 x

QUIZ!! Have a go at the 4 bit Hamming Checks quiz on Godalming Online before you move on!

4 bit Creation Example - 1101 Position n 7 6 5 4 3 2 1 What’s There Data Bit 4 Data Bit 3 Data Bit 2 Parity Bit 3 (P 3) Data Bit 1 Parity Bit 2 (P 2) Parity Bit 1 (P 1) 1 1 0 1 1 the 4 data 1 bits in the 0 correct positions • Start by placing 1 • Leave spaces for the parity bits • Parity bit 1 is 1 in position 11 1 1 0 • So it is part of 1 the pattern 1, 3, 5, 7 0 (check 1, skip 1) 1 0 • Parity bit 2 is in position 2 0 1 • this has the bits 101 currently so we add a 0 to keep even parity 1 2, 3, 6, 7 0(check 2, skip 0 2) 1 1 • So it is part of 1 the pattern 0 • The this Final has 111 sent currently we add a 1 to keep even parity Parity bit the 3 bit isbits pattern in position 4 is… so 1100110 • This So it includes is part ofthe 4 pattern data bits 4, 5, 6, 7 and three (check parity 4, skip bits 4) (although we only have 7 bits) • this has the bits 110 currently so we add a 0 to keep even parity

Why Bother? • This seems A LOT of processing and redundant data just to validate a nibble • Hamming Codes can “FIX” one bit of incorrect data!!!!! • Hamming is an ERROR CORRECTION code

Remember this • I get sent a 7 bit binary word: 0001101 • Need to check that there is even parity for each of the three parity bit pattern Position 7 6 5 4 3 2 1 n Word 0 0 0 1 1 0 1 P 1 0 1 so… Start at 01, check 1, skip 1, 1 check 1 skip 1 etc. . (1, 3, 5, 7) 1 P 1 is in position P 2 is in position Start at P 3 2 checkdon’t 2, skip 2 check 2 skip 2 rtc. . (2, 3, 6, 7) P 22 so…and have P 3 is in position 4 so…Start at 4, check 4 skip 4(then we run out of bits) (4, 5, 6, 7) P 2 P 3 0 0 1 0 “Even Parity” so this is 0 NOT 0 a 0 correct 1 pattern x x

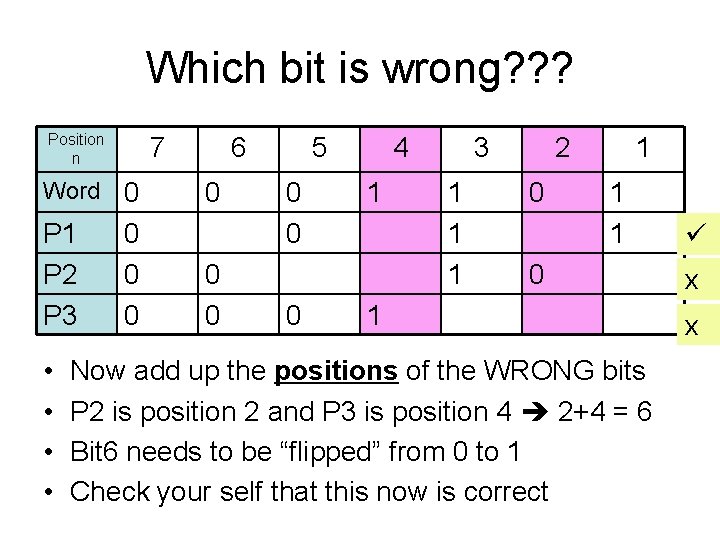
Which bit is wrong? ? ? Position n 7 Word 0 P 1 P 2 P 3 • • 0 0 0 6 0 0 0 5 0 0 0 4 1 3 1 1 1 2 0 1 1 1 0 1 Now add up the positions of the WRONG bits P 2 is position 2 and P 3 is position 4 2+4 = 6 Bit 6 needs to be “flipped” from 0 to 1 Check your self that this now is correct x x

NOW • Try changing another data bi in the Patten and see if the hamming • Have a go at the example in B&L