Hamiltoniano di spin Spin hamiltonian A useful resting







![Zero field splitting H= D[S 1 z 2 -S 1(S 1+1)/3]+ E(S 1 x Zero field splitting H= D[S 1 z 2 -S 1(S 1+1)/3]+ E(S 1 x](https://slidetodoc.com/presentation_image/3a4fbf937e145e39a4ce9294e611d99a/image-10.jpg)








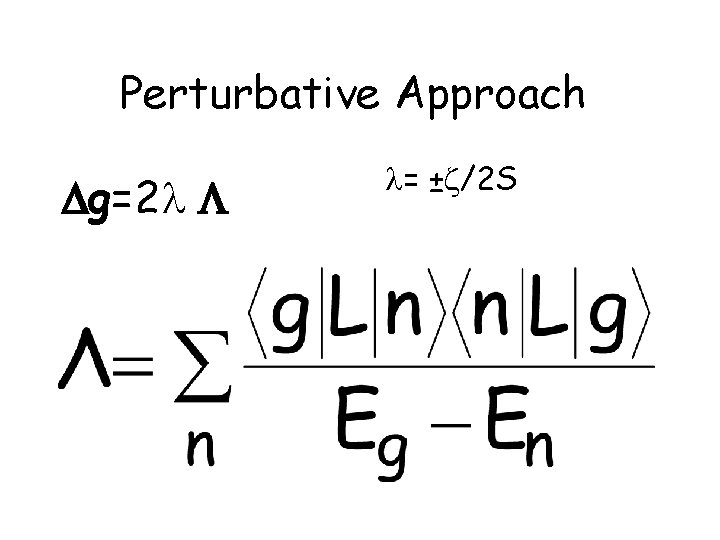


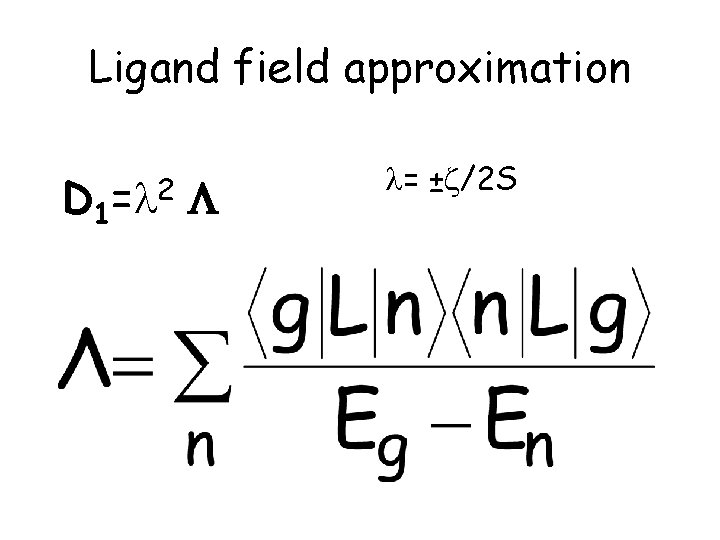
![A simpler treatment D=( /2)[gz-(gx+gy)/2]; E=( /4)[gx-gy] For tetragonally elongated Ni(II): gx= gy= 2. A simpler treatment D=( /2)[gz-(gx+gy)/2]; E=( /4)[gx-gy] For tetragonally elongated Ni(II): gx= gy= 2.](https://slidetodoc.com/presentation_image/3a4fbf937e145e39a4ce9294e611d99a/image-29.jpg)








- Slides: 41

Hamiltoniano di spin

Spin hamiltonian A useful resting place between fundamental theory and the squiggles of an oscilloscope Tutte le variabili elettroniche e nucleari sono sostituite da variabili di spin. I livelli energetici sono calcolati in modo parametrico

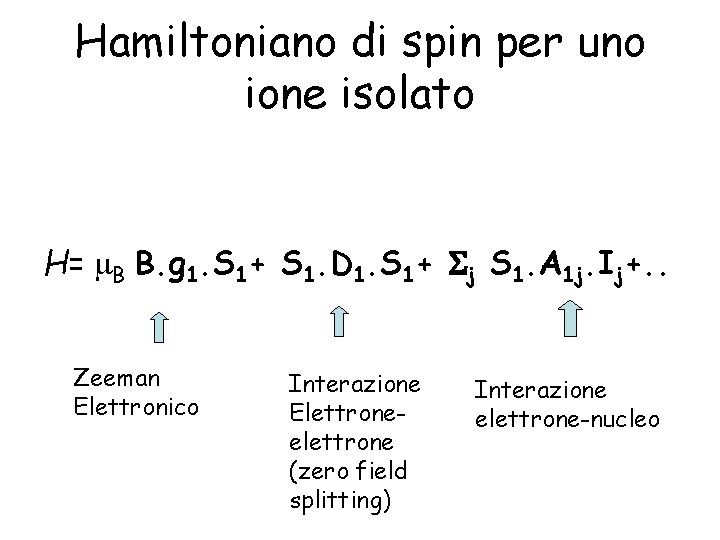
Hamiltoniano di spin per uno ione isolato H= B B. g 1. S 1+ S 1. D 1. S 1+ j S 1. A 1 j. Ij+. . Zeeman Elettronico Interazione Elettroneelettrone (zero field splitting) Interazione elettrone-nucleo

Stato orbitalmente non degenere Uno stato orbitalmente non degenere corrisponde ad una funzione reale. Lz è puramente immaginario ed è hermitiano, quindi deve avere autovalori reali Il risultato di operare con un operatore immaginario su una funzione reale deve essere immaginario o zero Quindi l’autovalore è zero

Zeeman Term In a system with quenched orbital moment, characterized by S= 1/2, when the static magnetic field H is parallel to z, the energy levels are given by: E(M)= g B MH 0 Similar expressions hold for x, and y. The anisotropy depends on the chemical environment, therefore it provides structural information

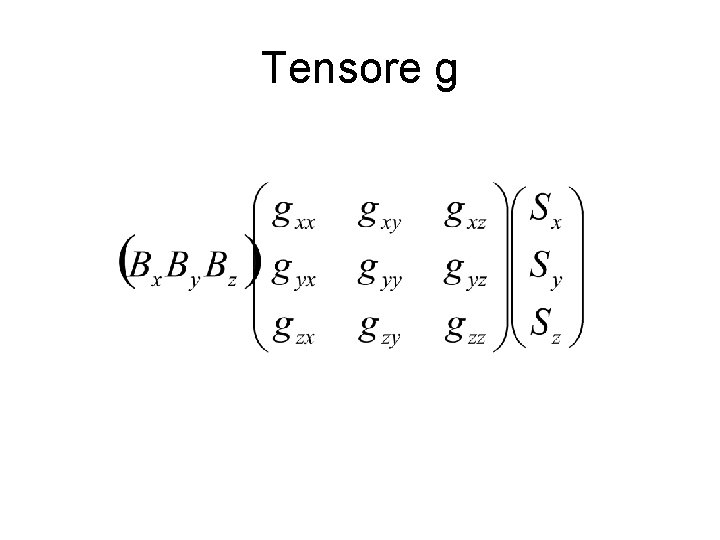
Tensore g

Per l’elettrone libero

Zeeman Splitting

Zero field splitting
![Zero field splitting H DS 1 z 2 S 1S 113 ES 1 x Zero field splitting H= D[S 1 z 2 -S 1(S 1+1)/3]+ E(S 1 x](https://slidetodoc.com/presentation_image/3a4fbf937e145e39a4ce9294e611d99a/image-10.jpg)
Zero field splitting H= D[S 1 z 2 -S 1(S 1+1)/3]+ E(S 1 x 2 -S 1 y 2) diagonale 0 E/D 1/3 Couples states differing in M by ± 2

Operatori di shift

Altre relazioni importanti

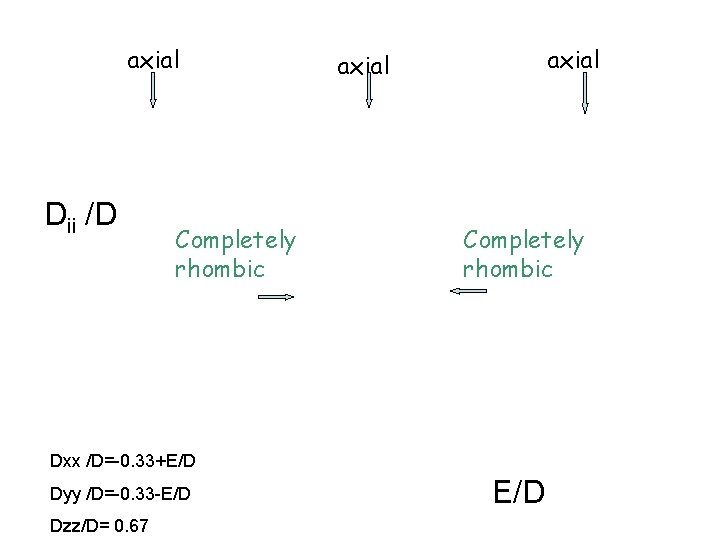
axial Dii /D Completely rhombic axial Completely rhombic Dxx /D=-0. 33+E/D Dyy /D=-0. 33 -E/D Dzz/D= 0. 67 E/D

Calcolare lo zfs di un tripletto

Energie in campo

Hamiltoniano vero

Al secondo ordine

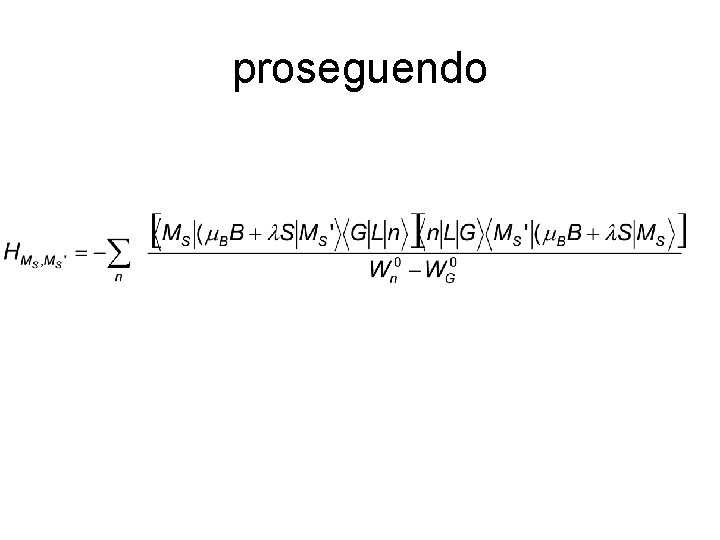
proseguendo

fattorizzando

Hamiltoniano di spin
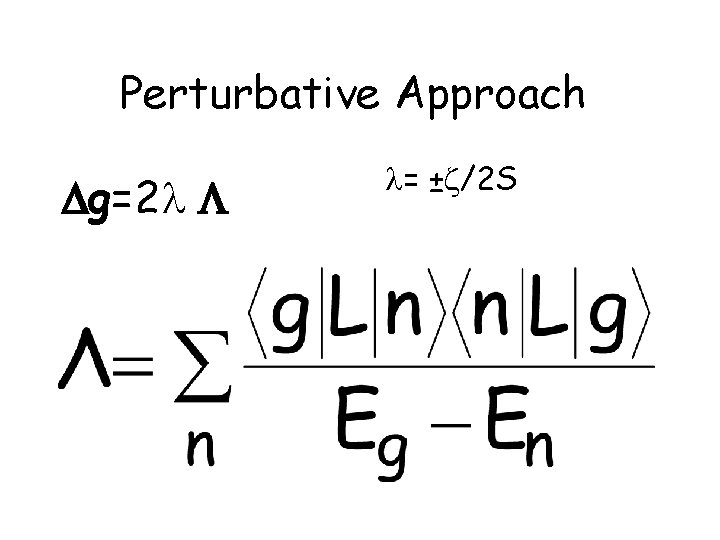
Perturbative Approach g=2 = ± /2 S

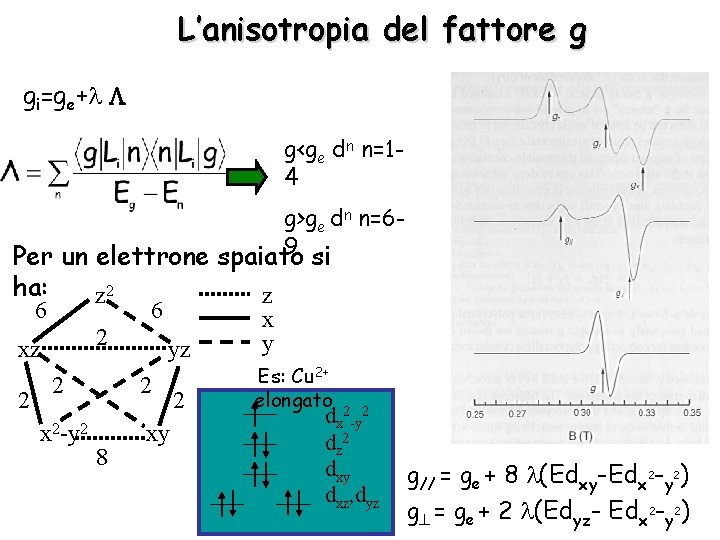
L’anisotropia del fattore g gi=ge+ g<ge dn n=14 g>ge dn n=69 si Per un elettrone spaiato ha: z 2 xz 2 6 2 2 x 2 -y 2 6 yz 2 8 xy 2 z x y Es: Cu 2+ elongato dx 2 -y 2 dz 2 dxy dxz, dyz g// = ge + 8 (Edxy-Edx 2 -y 2) g = ge + 2 (Edyz- Edx 2 -y 2)

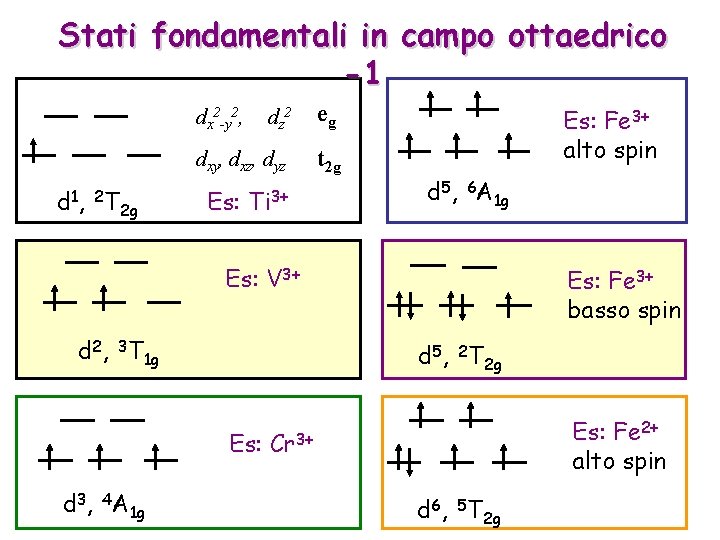
Stati fondamentali in campo ottaedrico -1 dz 2 eg dxy, dxz, dyz t 2 g dx 2 -y 2, d 1, 2 T 2 g Es: Ti 3+ Es: Fe 3+ alto spin d 5, 6 A 1 g Es: V 3+ d 2, 3 T 1 g d 5, 2 T 2 g Es: d 3, 4 A 1 g Es: Fe 3+ basso spin Es: Fe 2+ alto spin Cr 3+ d 6, 5 T 2 g

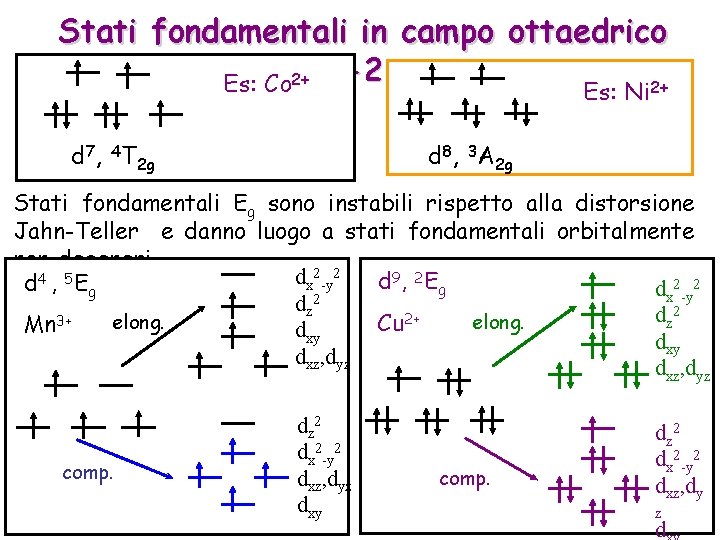
Stati fondamentali in campo ottaedrico Es: Co 2+ -2 2+ Es: Ni d 8, 3 A 2 g d 7, 4 T 2 g Stati fondamentali Eg sono instabili rispetto alla distorsione Jahn-Teller e danno luogo a stati fondamentali orbitalmente non-degeneri dx 2 -y 2 d 9, 2 E g 2 2 d 4 , 5 E g d x -y dz 2 2 dz 2+ elong. Cu Mn 3+ dxy dxz, dyz comp. dz 2 dx 2 -y 2 dxz, dyz dxy comp. dz 2 dx 2 -y 2 dxz, dy z d

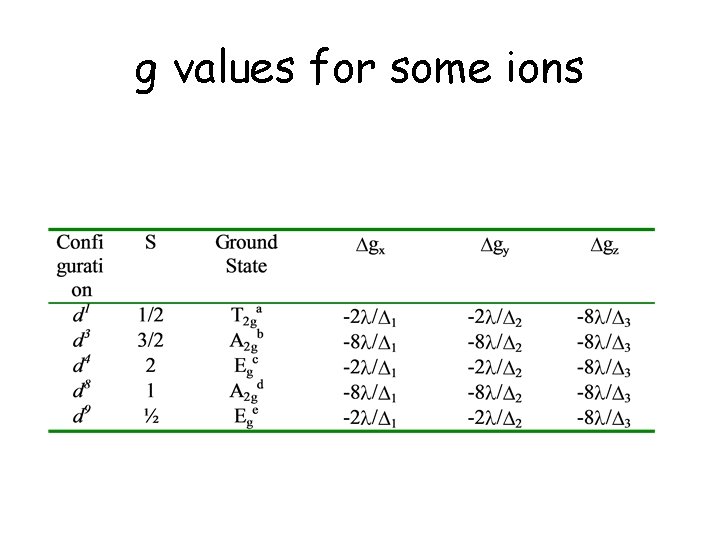
Valori di g per coordinazione pseudo-ottaedrica Conf. elett. d 1 d 2 d 3 d 4 S 1/2 1 3/2 2 d 5 HS d 6 d 7 5/2 2 3/2 d 8 d 9 1 1/2 Stato fond. 2 T 2 g 3 T 1 g 4 A 2 g 5 E comp. g elong. 6 A 1 g 5 T 2 g 4 T 2 g Oh elong. comp. 3 A 2 g 2 E elong. g comp. gx ge-2 / 1 ge-9 / ge-8 / 1 ge-6 / 1 ge-2 / 1 ge ge+2 / 1 2(5 - )/3 0 4 ge+8 / 1 ge+2 / 1 ge+6 / 1 gy ge-2 / 2 ge-9 / ge-8 / 2 ge-6 / 2 ge-2 / 2 ge ge+2 / 2 2(5 - )/3 0 4 ge+8 / 2 ge+2 / 2 ge+6 / 2 gz ge-8 / 3 ge ge+2 / 3 2(5 - )/3 2(3 - )/3 2 ge+8 / 3 ge

g values for some ions

Origine dello zero field splitting Per radicali organici: interazione dipolare elettrone Per ioni di transizione e terre rare: accoppiamento spin-orbita
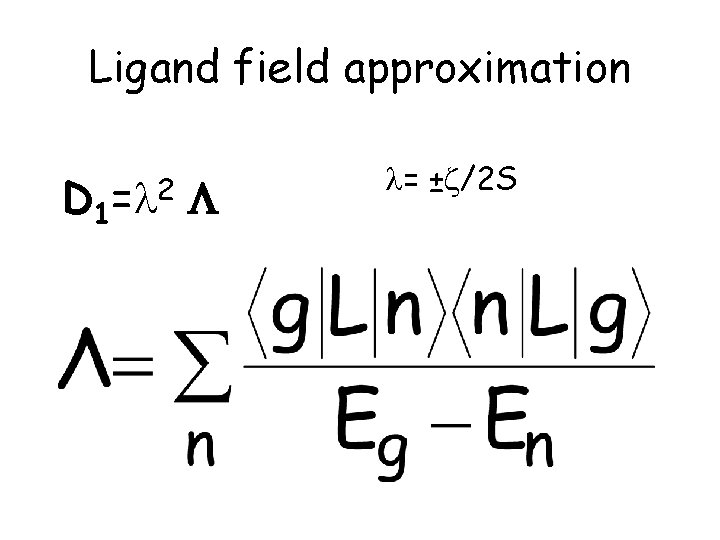
Ligand field approximation D 1 = 2 = ± /2 S
![A simpler treatment D 2gzgxgy2 E 4gxgy For tetragonally elongated NiII gx gy 2 A simpler treatment D=( /2)[gz-(gx+gy)/2]; E=( /4)[gx-gy] For tetragonally elongated Ni(II): gx= gy= 2.](https://slidetodoc.com/presentation_image/3a4fbf937e145e39a4ce9294e611d99a/image-29.jpg)
A simpler treatment D=( /2)[gz-(gx+gy)/2]; E=( /4)[gx-gy] For tetragonally elongated Ni(II): gx= gy= 2. 25; gz= 2. 24; =-315 cm-1 D= 1. 57 cm-1

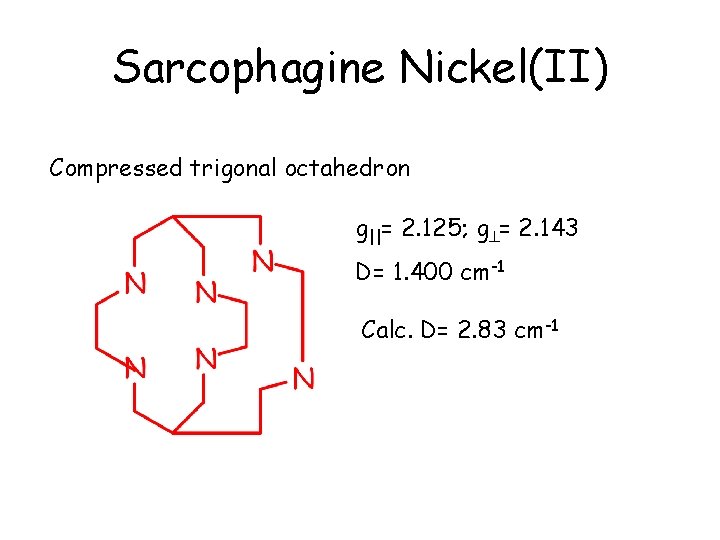
Sarcophagine Nickel(II) Compressed trigonal octahedron g||= 2. 125; g = 2. 143 D= 1. 400 cm-1 Calc. D= 2. 83 cm-1

Termini di ordine superiore Sono convenientemente descritti dagli operatori equivalenti di Stevens: H= n k Bnk Onk operator n=0, 2, 4, . . 2 S; k=-n, n parameter

Vantaggi degli operatori di Stevens • Sfruttano a dovere la simmetria: calcoli relativamente facili • Il numero di termini da includere è definito per simmetria • Per un asse C 4 di quantizzazione solo i termini k= 0 and k= 4 devono essere inclusi • Per C 2, k=0, 2, 4 • Gli operatori Onk accoppiano stati che differiscono in M di ±k

Alcuni esempi di operatori n=2 O 20=3 Sz 2 -S(S+1) D=3 B 20; E=B 22 O 22=(S+2+S-2) n=4 O 40 =35 Sz 4 -30 S(S+1)Sz 2+25 Sz 2 -6 S(S+1)+3 S 2(S+1)2 O 42={(7 Sz 2 -S(S+1)-5)(S+2+S-2)}S/2 O 43={Sz(S+3+S-3)}S/2 O 44=(S+4+S-4)/2 {A, B}S=(AB+BA)/2

Ask him the program! Quantitative LF Approach Bencini, A. ; Ciofini, I. ; Uytterhoeven, M. G. Inorg. Chim. Acta 1998, 274, 90 The energies of the LF levels are calculated using a full matrix diagonalization approach. The SH parameters, in principle to any order, are obtained by best fit of the calculated energies. Both classic crystal field and Angular Overlap parametrization can be used

Manganese(III) Compressed z 2 x 2 -y 2 Elongated x 2 -y 2 z 2

Manganese(III): SH Parameters Compressed: Elongated: gz= 2. 00; gx=1. 97 gz= 1. 96; gx=1. 99 D= 4. 72 cm-1 D= -4. 83 cm-1 B 20= 3. 854 cm-1 B 20=-3. 948 cm-1 B 40=-9. 82 10 -3 cm-1 B 40=-6. 70 10 -5 cm-1 B 44=5. 18 10 -3 cm-1 B 44=1. 86 10 -3 cm-1 Dq=1600 cm-1

HS Iron(III): SH Parameters for Tetragonal Distortion Compressed: Elongated: gz= 2. 00; gx=2. 00 gz= 2. 00; gx=1. 97 D= -0. 282 cm-1 D= 0. 308 cm-1 B 20=-0. 230 cm-1 B 20= 0. 252 cm-1 B 40= 6. 24 10 -3 cm-1 B 40= 7. 17 10 -3 cm-1 B 44=4. 66 10 -3 cm-1 B 44= 6. 75 10 -3 cm-1

HS Iron(III): SH Parameters for Trigonal Distortion Compressed: Elongated: gz= 2. 00; gx=2. 00 gz= 2. 00; gx=1. 97 D= 0. 156 cm-1 D= -0. 144 cm-1 B 20= 0. 127 cm-1 B 20= -0. 117 cm-1 B 40= -4. 479 10 -3 cm-1 B 40= -4. 284 10 -3 cm-1 B 44= -7. 153 10 -3 cm-1 B 44= -7. 253 10 -3 cm-1

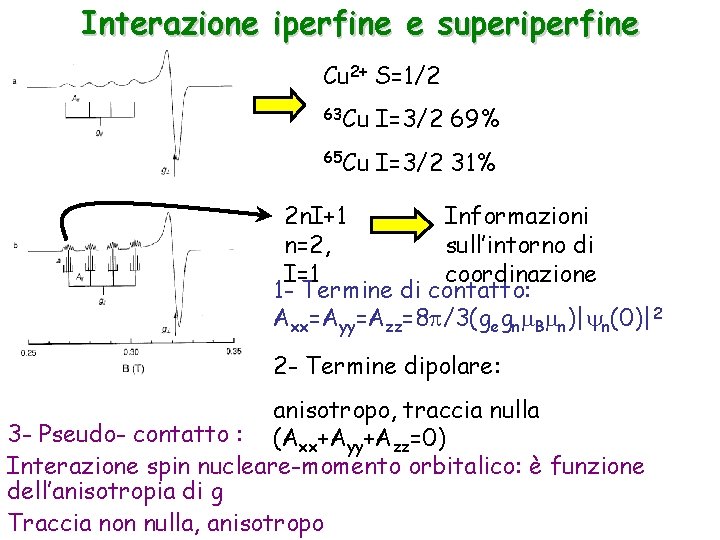
Interazione iperfine e superiperfine Cu 2+ S=1/2 63 Cu I=3/2 69% 65 Cu I=3/2 31% 2 n. I+1 Informazioni n=2, sull’intorno di I=1 coordinazione 1 - Termine di contatto: Axx=Ayy=Azz=8 /3(gegn B n)| n(0)|2 2 - Termine dipolare: anisotropo, traccia nulla 3 - Pseudo- contatto : (Axx+Ayy+Azz=0) Interazione spin nucleare-momento orbitalico: è funzione dell’anisotropia di g Traccia non nulla, anisotropo

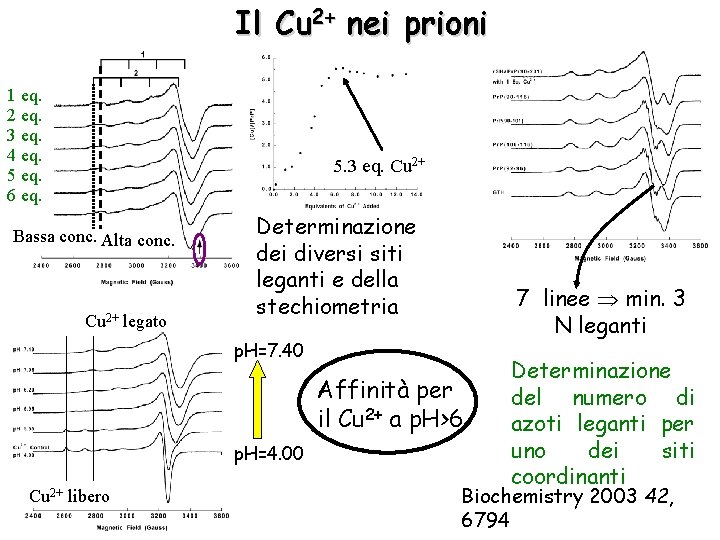
Il Cu 2+ nei prioni 1 eq. 2 eq. 3 eq. 4 eq. 5 eq. 6 eq. 5. 3 eq. Cu 2+ Bassa conc. Alta conc. Cu 2+ legato Determinazione dei diversi siti leganti e della stechiometria 7 linee min. 3 N leganti p. H=7. 40 Affinità per il Cu 2+ a p. H>6 p. H=4. 00 Cu 2+ libero Determinazione del numero di azoti leganti per uno dei siti coordinanti Biochemistry 2003 42, 6794

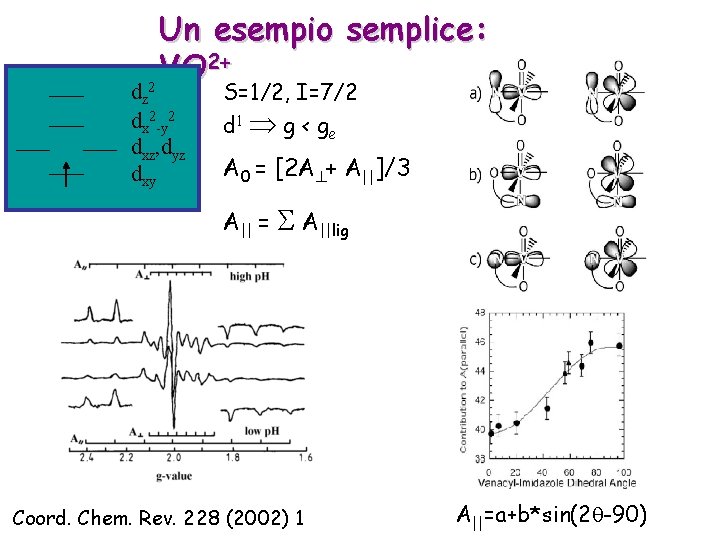
Un esempio semplice: 2+ VO 2 dz dx 2 -y 2 dxz, dyz dxy S=1/2, I=7/2 d 1 g < g e A 0 = [2 A + A||]/3 A|| = A||lig Coord. Chem. Rev. 228 (2002) 1 A||=a+b*sin(2 -90)