HAMILTONIAN STRUCTURE OF THE PAINLEVE EQUATIONS HAMILTONIAN STRUCTURE

















































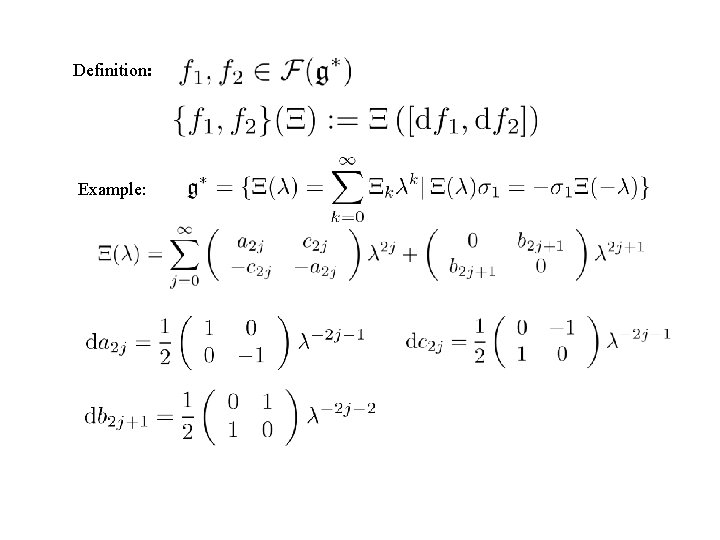
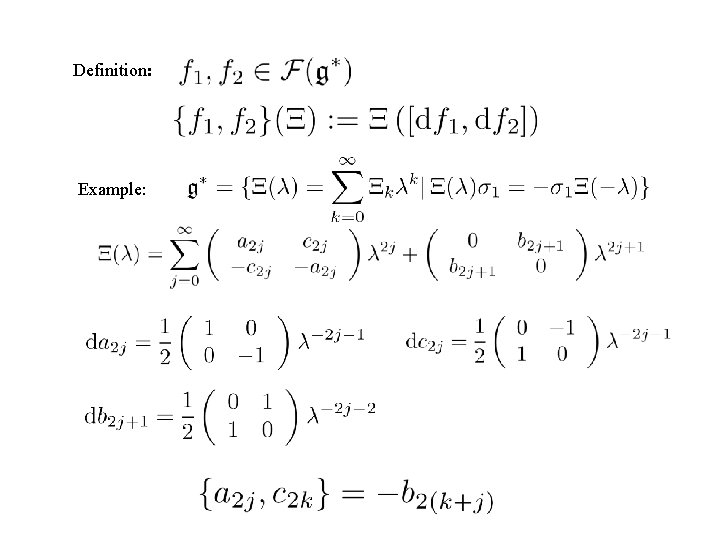





- Slides: 56

HAMILTONIAN STRUCTURE OF THE PAINLEVE’ EQUATIONS

HAMILTONIAN STRUCTURE OF THE PAINLEVE’ EQUATIONS • Hamiltonian formulation:

HAMILTONIAN STRUCTURE OF THE PAINLEVE’ EQUATIONS • Hamiltonian formulation:

HAMILTONIAN STRUCTURE OF THE PAINLEVE’ EQUATIONS • Hamiltonian formulation: Example: PII

HAMILTONIAN STRUCTURE OF THE PAINLEVE’ EQUATIONS • Hamiltonian formulation: Example: PII • Isomonodromic deformations method (IMD):

HAMILTONIAN STRUCTURE OF THE PAINLEVE’ EQUATIONS • Hamiltonian formulation: Example: PII • Isomonodromic deformations method (IMD):

HAMILTONIAN STRUCTURE OF THE PAINLEVE’ EQUATIONS • Hamiltonian formulation: Example: PII • Isomonodromic deformations method (IMD):

HAMILTONIAN STRUCTURE OF THE PAINLEVE’ EQUATIONS • Hamiltonian formulation: Example: PII • Isomonodromic deformations method (IMD): Example: PII

In this course we shall see how to deduce the Hamiltonian formulation from the IMD.

In this course we shall see how to deduce the Hamiltonian formulation from the IMD. Motivation: find the Hamiltonian structure of more complicated generalizations of the Painleve’ equations

In this course we shall see how to deduce the Hamiltonian formulation from the IMD. Motivation: find the Hamiltonian structure of more complicated generalizations of the Painleve’ equations Example: PII (2) What are p 1 , p 2, q 1, q 2 in this case? What is H?

In this course we shall see how to deduce the Hamiltonian formulation from the IMD. Motivation: find the Hamiltonian structure of more complicated generalizations of the Painleve’ equations Example: PII (2) What are p 1 , p 2, q 1, q 2 in this case? What is H? Literature: Adler-Kostant-Symes, Adams-Harnad-Hurtubise, Gehktman, Hitchin, Krichever, Novikov-Veselov, Scott, Sklyanin……………. . Recent books: Adler-van Moerbeke-Vanhaeke Babelon-Bernard-Talon

Recap on Poisson and symplectic manifolds. (Arnol’d, Classical Mechanics)

Recap on Poisson and symplectic manifolds. (Arnol’d, Classical Mechanics) • M = phase space

Recap on Poisson and symplectic manifolds. (Arnol’d, Classical Mechanics) • M = phase space • F(M) = algebra of differentiable functions

Recap on Poisson and symplectic manifolds. (Arnol’d, Classical Mechanics) • M = phase space • F(M) = algebra of differentiable functions • Poisson bracket: {f, g} = -{g, f} { , }: F(M) x F(M) -> F(M) skewsymmetry {f, a g+ b h} = a {f, g} + b {f, h} {f, g h} = {f, g} h + {f, h} g linearity Libenitz {f, {g, h}} + {h, {f, g}} + {g, {h, f}} = 0 Jacobi

Recap on Poisson and symplectic manifolds. (Arnol’d, Classical Mechanics) • M = phase space • F(M) = algebra of differentiable functions • Poisson bracket: {f, g} = -{g, f} { , }: F(M) x F(M) -> F(M) skewsymmetry {f, a g+ b h} = a {f, g} + b {f, h} {f, g h} = {f, g} h + {f, h} g linearity Libenitz {f, {g, h}} + {h, {f, g}} + {g, {h, f}} = 0 • Vector field XH associated to H e. F(M): Jacobi XH(f): = {H, f}

Recap on Poisson and symplectic manifolds. (Arnol’d, Classical Mechanics) • M = phase space • F(M) = algebra of differentiable functions • Poisson bracket: {f, g} = -{g, f} { , }: F(M) x F(M) -> F(M) skewsymmetry {f, a g+ b h} = a {f, g} + b {f, h} {f, g h} = {f, g} h + {f, h} g linearity Libenitz {f, {g, h}} + {h, {f, g}} + {g, {h, f}} = 0 • Vector field XH associated to H e. F(M): Jacobi XH(f): = {H, f} A Posson manifold is a differentiable manifold M with a Poisson bracket { , }

Recap on Lie groups and Lie algebras

Recap on Lie groups and Lie algebras Lie group G: analytic manifold with a compatible group structure • multiplication: G x G --> G • inversion: G --> G

Recap on Lie groups and Lie algebras Lie group G: analytic manifold with a compatible group structure • multiplication: G x G --> G • inversion: G --> G Example:

Recap on Lie groups and Lie algebras Lie group G: analytic manifold with a compatible group structure • multiplication: G x G --> G • inversion: G --> G Example: Lie algebra g: vector space with Lie bracket • [x, y] = -[y, x] antisymmetry • [a x + b y, z] = a [x, z] + b [y, z] linearity • [x, [y, z]] + [z, [x, y]] + [y, [z, x]] = 0 Jacobi

Recap on Lie groups and Lie algebras Lie group G: analytic manifold with a compatible group structure • multiplication: G x G --> G • inversion: G --> G Example: Lie algebra g: vector space with Lie bracket • [x, y] = -[y, x] antisymmetry • [a x + b y, z] = a [x, z] + b [y, z] linearity • [x, [y, z]] + [z, [x, y]] + [y, [z, x]] = 0 Jacobi Example:

Adjoint and coadjoint action. • Given a Lie group G its Lie algebra g is Te G.

Adjoint and coadjoint action. • Given a Lie group G its Lie algebra g is Te G. Example: G = SL(2, C). Then

Adjoint and coadjoint action. • Given a Lie group G its Lie algebra g is Te G. Example: G = SL(2, C). Then • g acts on itself by the adjoint action:

Adjoint and coadjoint action. • Given a Lie group G its Lie algebra g is Te G. Example: G = SL(2, C). Then • g acts on itself by the adjoint action: • g acts on g* by the coadjoint action:

Example: • Symmetric non-degenerate bilinear form:

Example: • Symmetric non-degenerate bilinear form: • Coadjoint action:

Example: • Symmetric non-degenerate bilinear form: • Coadjoint action:

Example: • Symmetric non-degenerate bilinear form: • Coadjoint action:

Loop algebra

Loop algebra • Commutator:

Loop algebra • Commutator: • Killing form:

Loop algebra • Commutator: • Killing form: • Subalgebra:

Loop algebra • Commutator: • Killing form: • Subalgebra: • Dual space:

Loop algebra • Commutator: • Killing form: • Subalgebra: • Dual space:

Loop algebra • Commutator: • Killing form: • Subalgebra: • Dual space:

Coadjoint orbits

Coadjoint orbits Integrable systems = flows on coadjoint orbits:

Coadjoint orbits Integrable systems = flows on coadjoint orbits: Example: PII

Coadjoint orbits Integrable systems = flows on coadjoint orbits: Example: PII

Coadjoint orbits Integrable systems = flows on coadjoint orbits: Example: PII

Kostant - Kirillov Poisson bracket on the dual of a Lie algebra

Kostant - Kirillov Poisson bracket on the dual of a Lie algebra • Differential of a function

Kostant - Kirillov Poisson bracket on the dual of a Lie algebra • Differential of a function Example: PII. Take

Definition:

Definition: Example:

Definition: Example:
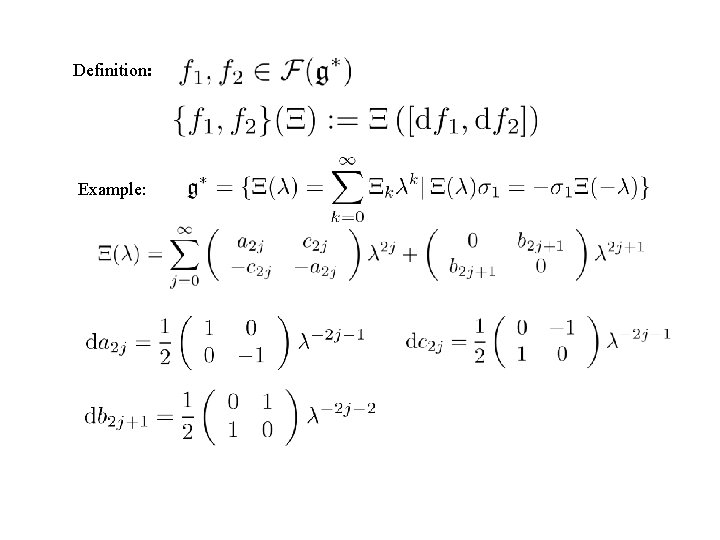
Definition: Example:
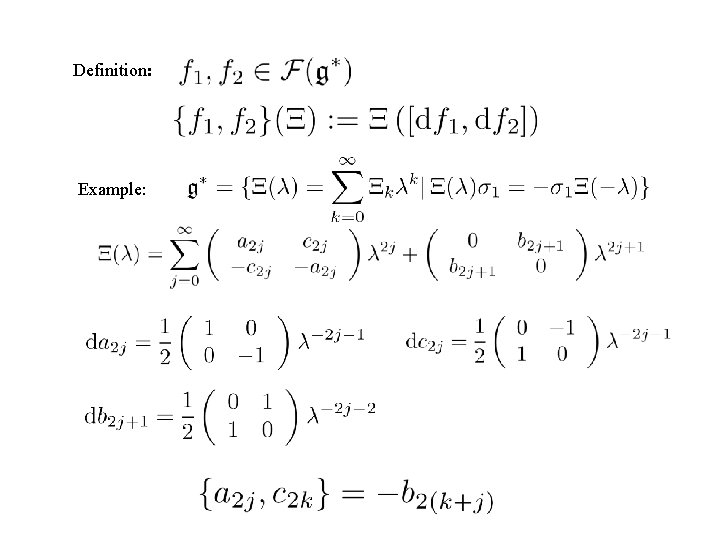
Definition: Example:

Hamiltonians

Hamiltonians • Fix a function

Hamiltonians • Fix a function • For every define:

Hamiltonians • Fix a function • For every define: • Kostant Kirillov Poisson bracket:

Hamiltonians • Fix a function • For every define: • Kostant Kirillov Poisson bracket: • Define then we get the evolution equation: