Hamiltonian quantum computer in one dimension TzuChieh Wei

Hamiltonian quantum computer in one dimension Tzu-Chieh Wei C. N. Yang Institute for Theoretical Physics Department of Physics & Astronomy John C Liang Rumson-Fair High School Stanford University AQIS, Taipei, 8/30/2016 Supported by

Outline I. Introduction: Hamiltonian quantum computer II. 1 D 3 -local 5 -state construction (not translation invariant) III. 1 D 3 -local 8 -state construction (translation invariant) [will not have much time for this part] IV. Summary

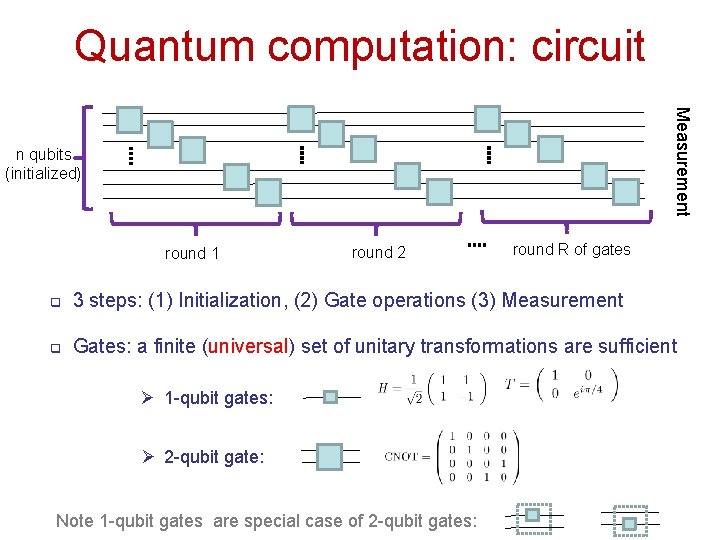
Quantum computation: circuit Measurement n qubits (initialized) round 1 round 2 round R of gates q 3 steps: (1) Initialization, (2) Gate operations (3) Measurement q Gates: a finite (universal) set of unitary transformations are sufficient Ø 1 -qubit gates: Ø 2 -qubit gate: Note 1 -qubit gates are special case of 2 -qubit gates:

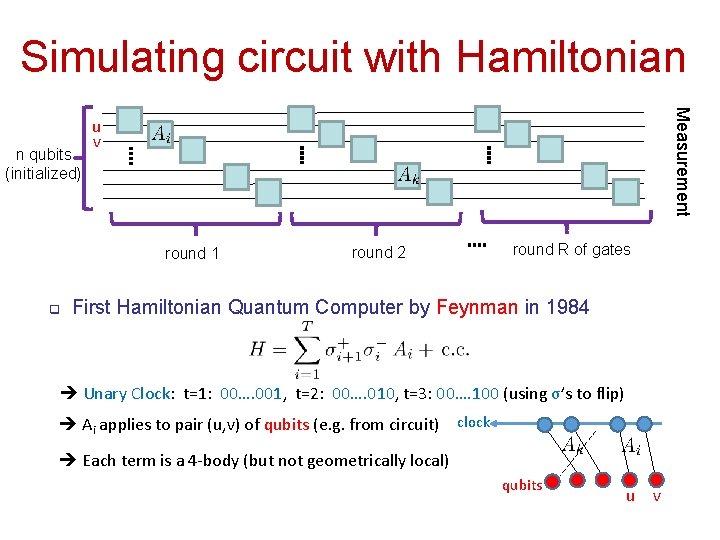
Simulating circuit with Hamiltonian Measurement n qubits (initialized) u v round 1 q round 2 round R of gates First Hamiltonian Quantum Computer by Feynman in 1984 Unary Clock: t=1: 00…. 001, t=2: 00…. 010, t=3: 00…. 100 (using σ’s to flip) Ai applies to pair (u, v) of qubits (e. g. from circuit) clock Each term is a 4 -body (but not geometrically local) qubits u v

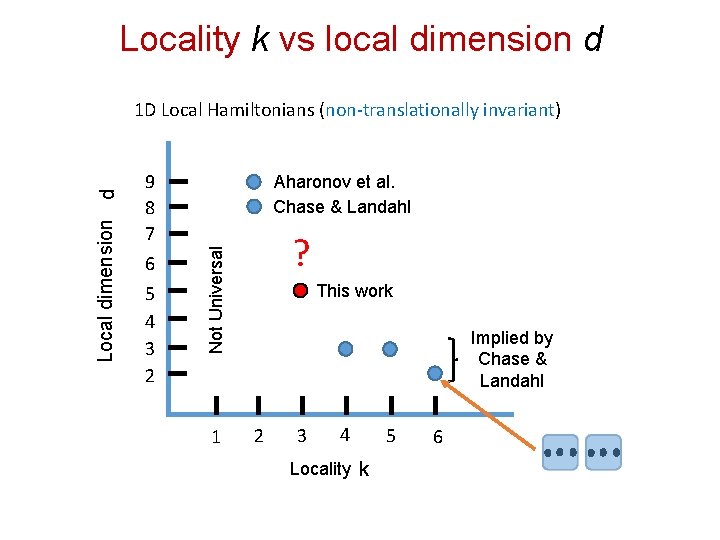
1 D Hamiltonian Quantum Computer q Can we do this with a one-dimensional Hamiltonian? (Feynman’s not 1 D) q Yes: but requires large local dimension for short-ranged, e. g. nearest-neighbor: Ø Vollbrecht & Cirac: translation invariant, 30 -state Ø Kay: translation invariant, 31 -state Ø Nagaj & Wocjan: translation invariant, (1) 10 -state (2) 20 -state Ø Aharonov et al. has one construction that (can be interpreted in terms of Hamiltonian QC) is non-translation invariant with 9 -state Ø Chase & Landahl: non-translation invariant, 8 -state

Locality k vs local dimension d 9 8 7 6 5 4 3 2 Aharonov et al. Chase & Landahl ? Not Universal Local dimension d 1 D Local Hamiltonians (non-translationally invariant) 1 This work Implied by Chase & Landahl 2 3 4 Locality k 5 6

Outline I. Introduction: Hamiltonian quantum computer II. 1 D 3 -local 5 -state construction (not translation invariant) III. 1 D 3 -local 8 -state construction (translation invariant) IV. Summary

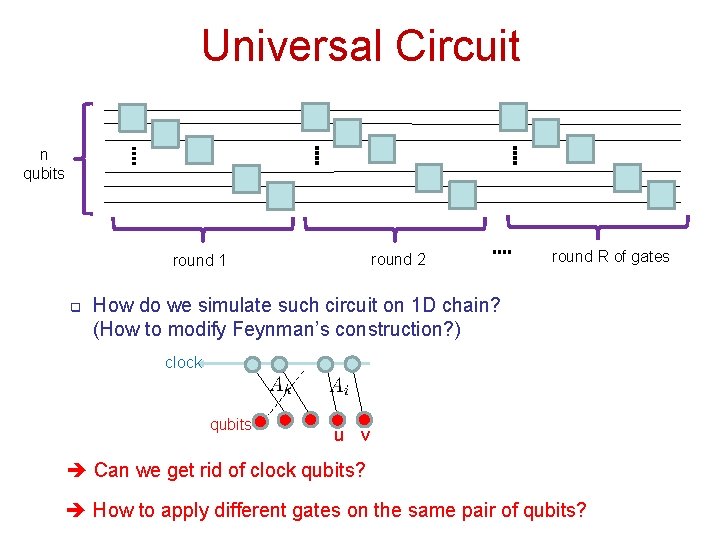
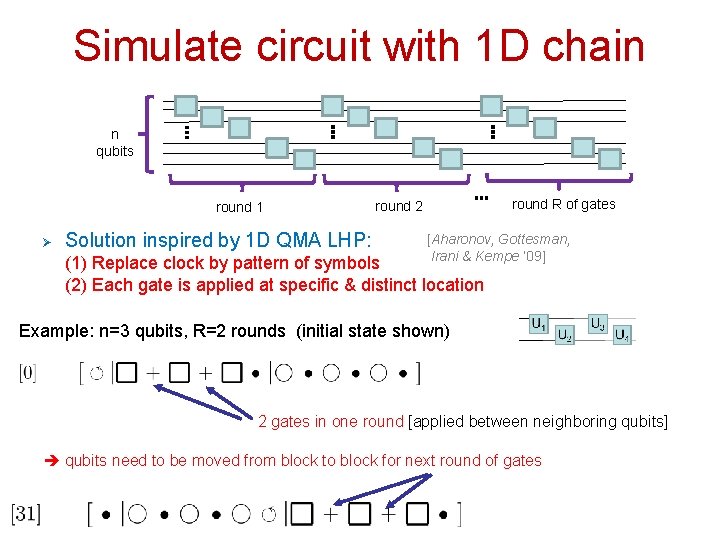
Universal Circuit n qubits round 2 round 1 q round R of gates How do we simulate such circuit on 1 D chain? (How to modify Feynman’s construction? ) clock qubits u v Can we get rid of clock qubits? How to apply different gates on the same pair of qubits?

Simulate circuit with 1 D chain n qubits round 1 Ø Solution inspired by 1 D QMA LHP: round R of gates round 2 [Aharonov, Gottesman, Irani & Kempe ‘ 09] (1) Replace clock by pattern of symbols (2) Each gate is applied at specific & distinct location Example: n=3 qubits, R=2 rounds (initial state shown) 2 gates in one round [applied between neighboring qubits] qubits need to be moved from block to block for next round of gates

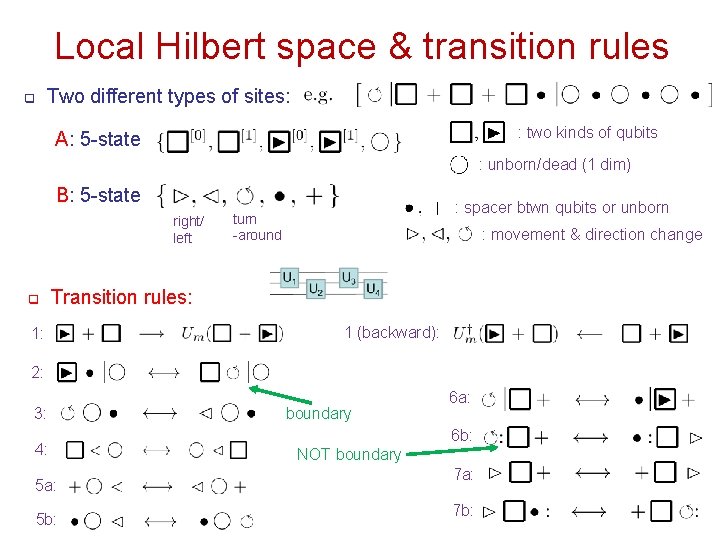
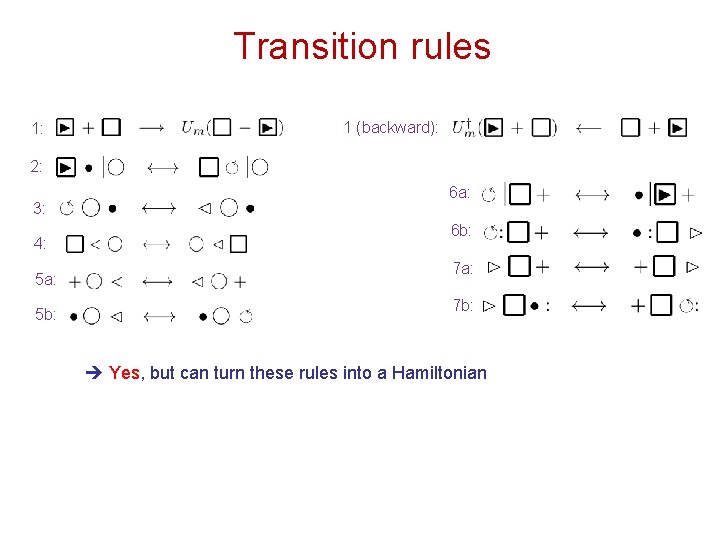
Local Hilbert space & transition rules q Two different types of sites: : two kinds of qubits A: 5 -state : unborn/dead (1 dim) B: 5 -state right/ left q : spacer btwn qubits or unborn turn -around : movement & direction change Transition rules: 1 (backward): 2: 3: 4: 5 a: 5 b: boundary 6 a: 6 b: NOT boundary 7 a: 7 b:

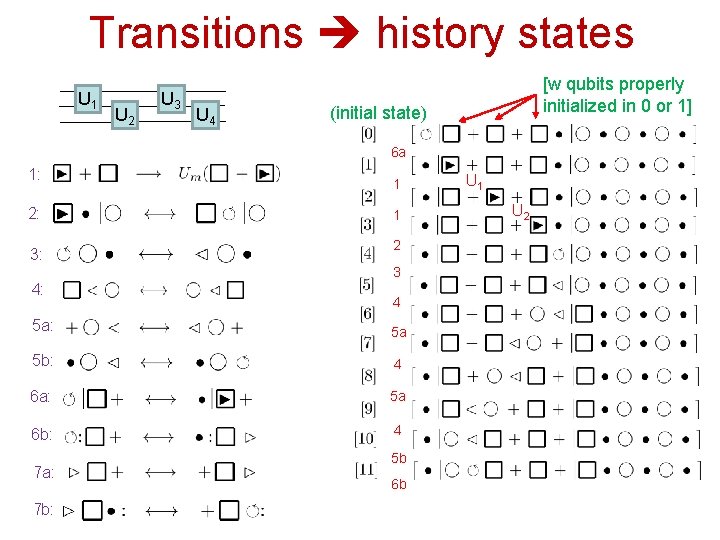
Transitions history states U 1 U 2 U 3 U 4 [w qubits properly initialized in 0 or 1] (initial state) 6 a 1: 2: 3: 1 1 2 3 4: 4 5 a: 5 a 5 b: 4 6 a: 5 a 6 b: 4 7 a: 7 b: 5 b 6 b U 1 U 2

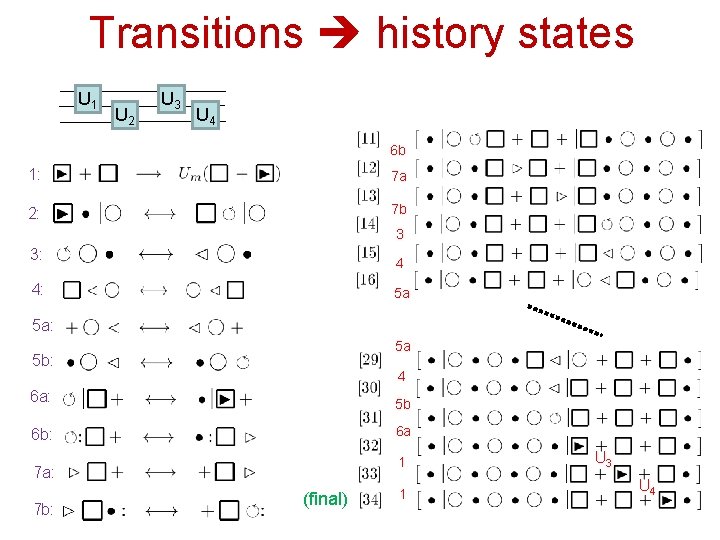
Transitions history states U 1 U 2 U 3 U 4 6 b 1: 7 a 2: 7 b 3 3: 4 4: 5 a 5 a: 5 a 5 b: 4 6 a: 5 b 6 b: 6 a 1 7 a: 7 b: (final) 1 U 3 U 4

Computation at discrete time & history states U 1 U 2 U 3 U 4 q 6 a 1 1 Unique forward/backward transition (except at initial and final state) U 1 U 2 q 2 Transition rules uniquely connect history states (of computation) 3 5 a But isn’t our computer run by continuous-time evolution? Hamiltonian? q 4 5 b 6 a 1 1 U 3 U 4

Transition rules 1: 1 (backward): 2: 3: 4: 5 a: 5 b: 6 a: 6 b: 7 a: 7 b: Yes, but can turn these rules into a Hamiltonian

Hamiltonian q Constructed from the transition rules: q In the basis of valid history (via transition rules): Effective Hamiltonian:

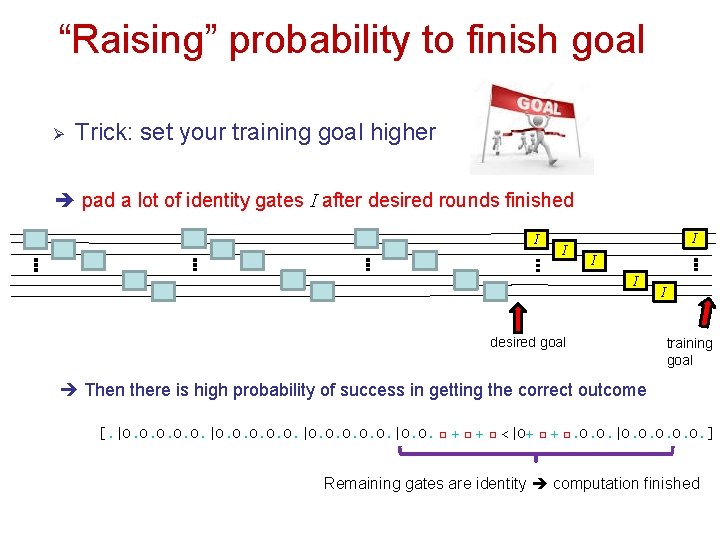
Run your Hamiltonian computer [@|□+ □ + □ + □. |O. O. O. ] q With qubits appropriately initialized (e. g. 00000) q Quantum computation: evolve by Schrodinger equation via Hamiltonian q Readout: measure in the “computational basis” Problems: But at what time t ? We want it to evolve to final state! Naïve counting: probability 1/T to land onto the final state!!

“Raising” probability to finish goal Ø Trick: set your training goal higher pad a lot of identity gates I after desired rounds finished III I I desired goal I training goal Then there is high probability of success in getting the correct outcome [. |O. O. O. |O. O. □ + □ <|O+ □ + □. O. O. |O. O. O. ] Remaining gates are identity computation finished

Effective Hamiltonian: 1 D “quantum walk” or tight-binding model has eigenvalues with eigenstates q Starting at |0›, probability of arriving at |m› after time τ

Analysis for success probability q Starting at |0›, probability of arriving at |m› after time τ q Can show that [Nagaj & Wocjan, PRA 2008] q Pad sufficient identity gates (e. g. 5 times as many) so that for m ≥ T/6, desired computation is done q Readout: measure in the basis at random time A: B: e. g. [. |O. O. O. |O. O. □ + □ <|O+ □ + □. O. O. |O. O. O. ] q Take finite and high probability of success

So we have demonstrated a 1 D 3 -local 5 -state (spin-2) Hamiltonian capable of universal QC Classical simulation of such spin-2 Hamiltonian is BQP-complete

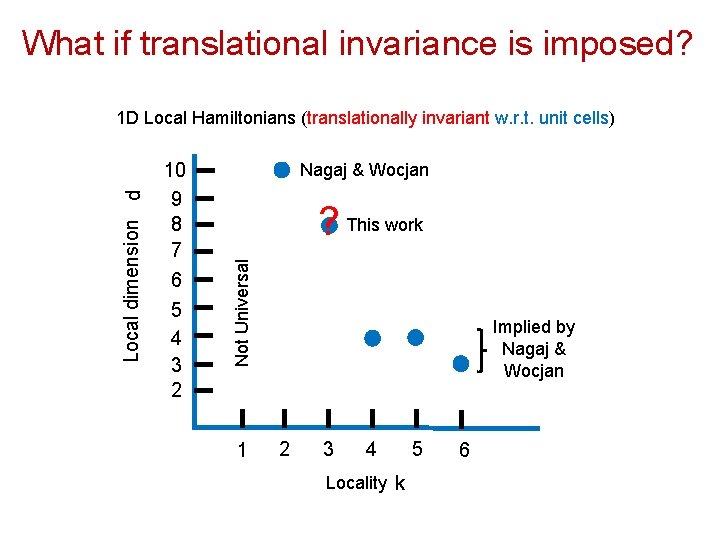
What if translational invariance is imposed? 10 9 8 7 6 5 4 3 2 Nagaj & Wocjan ? This work Not Universal Local dimension d 1 D Local Hamiltonians (translationally invariant w. r. t. unit cells) 1 Implied by Nagaj & Wocjan 2 3 4 Locality k 5 6

Summary & open questions q 1 D 3 -local 5 -state (spin-2) Hamiltonian (not translationally invariant) universal for Hamiltonian quantum computation q 1 D 3 -local 8 -state (spin-7/2) Hamiltonian (translationally invariant) universal for Hamiltonian quantum computation q Open: are the above results optimal? q What about 1 D 3 -local QMA Hamiltonians? Minimum local dim?