Hamiltonian Circuits and Paths Section 4 5 Sir

Sir William Rowan Hamilton ► Irish Mathematician ► Knighted at the age of 30

Icosian Game ► Vertices were meant to represent major cities in Europe. ► Goal

Street Example ► Remember when we had the street network and we wanted to

Hamiltonian Paths and Circuits ► Hamiltonian path: You cross each vertex exactly once and

So is there an easy rule? ? ► There is not an easy rule,

Does it work? We are guaranteed to have a Hamiltonian Circuit. Downfall: That doesn’t

Does it work? We are not guaranteed a Hamilton circuit, but there is one.

Find the Hamiltonian Circuit We are not guaranteed that there is a Hamiltonian circuit.

State which graphs are guaranteed to have a Hamiltonian circuit

Let’s do another online quiz… ► http: //primes. utm. edu/cgi- bin/caldwell/tutor/graph/euler

Tournaments ► By using directed edges, we can indicate winners and losers in a

Example ► List the winners of each game. A B C

Why tournaments are cool! ► You can give a ranking for each team if

Example ► Draw a digraph for the following school soccer team round-robin tournament. ►

Example ► Draw a tournament with five players, in which player A defeats everyone,

Find all the directed Hamiltonian paths for the following tournaments. If there is only

Slides: 23

Download presentation

Hamiltonian Circuits and Paths Section 4. 5

Sir William Rowan Hamilton ► Irish Mathematician ► Knighted at the age of 30 ► Hamiltonian Mechanics are used to determine orbital trajectories of satellites. ► Came up with a game…

Icosian Game ► Vertices were meant to represent major cities in Europe. ► Goal is to visit all 20 cities. ► Let’s PLAY!!!!!!

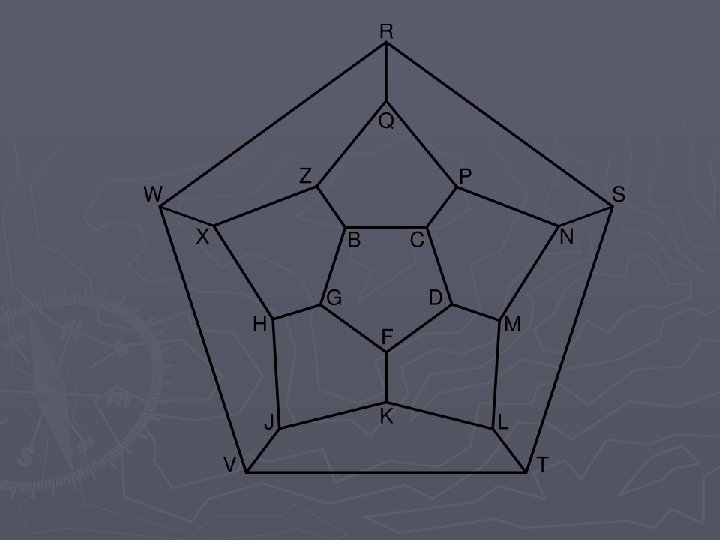
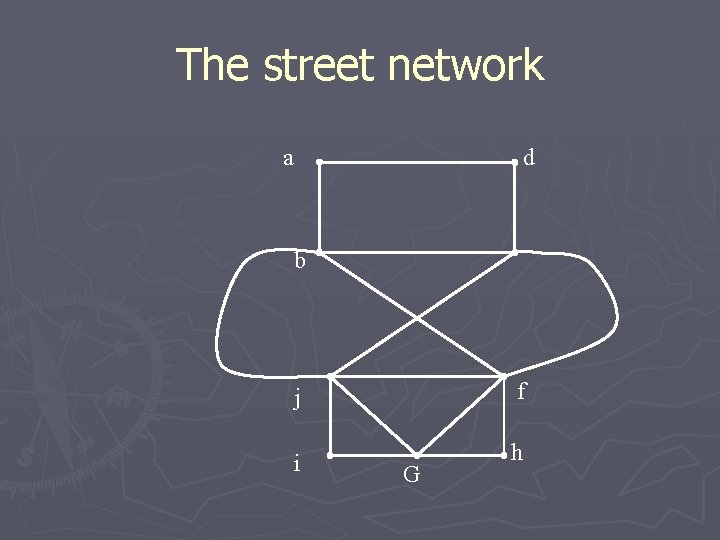
Street Example ► Remember when we had the street network and we wanted to inspect each street exactly once? Well now we need to inspect the fire hydrants (they are located at the intersections. What are the intersections on the graph? ► Can we start at the garage and stop at each intersection exactly once and return to the garage?

The street network a d b j f i h G

Hamiltonian Paths and Circuits ► Hamiltonian path: You cross each vertex exactly once and start and end at different places. ► Hamiltonian circuit: You cross each vertex exactly once and start and end at the same place.

Find the Hamiltonian Circuit

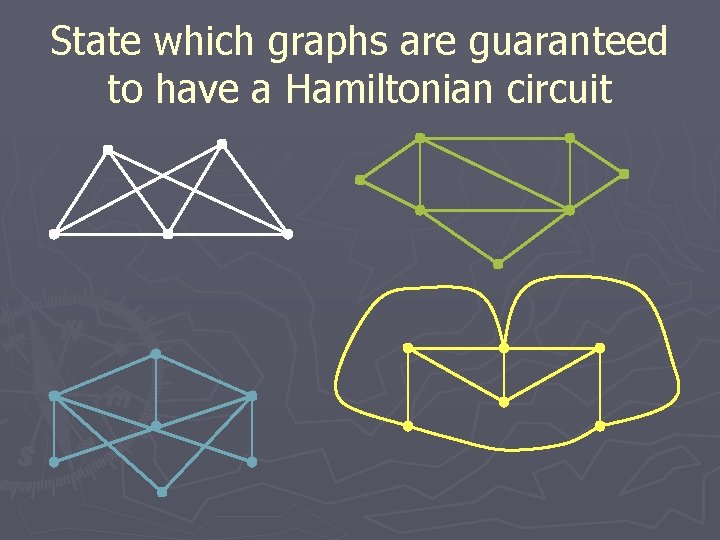
So is there an easy rule? ? ► There is not an easy rule, but there is a vague one. § If a connected graph has n vertices, where n > 2 and each vertex has a degree of at least n/2, then the graph has a Hamiltonian circuit.

Does it work? We are guaranteed to have a Hamiltonian Circuit. Downfall: That doesn’t mean we now know how to find it.

Does it work? We are not guaranteed a Hamilton circuit, but there is one. Downfall: We don’t know if there is a Hamiltonian circuit.

Find the Hamiltonian Circuit We are not guaranteed that there is a Hamiltonian circuit. We can’t tell by theorem that there is not one. We had to use trial and error.

State which graphs are guaranteed to have a Hamiltonian circuit

Let’s do another online quiz… ► http: //primes. utm. edu/cgi- bin/caldwell/tutor/graph/euler

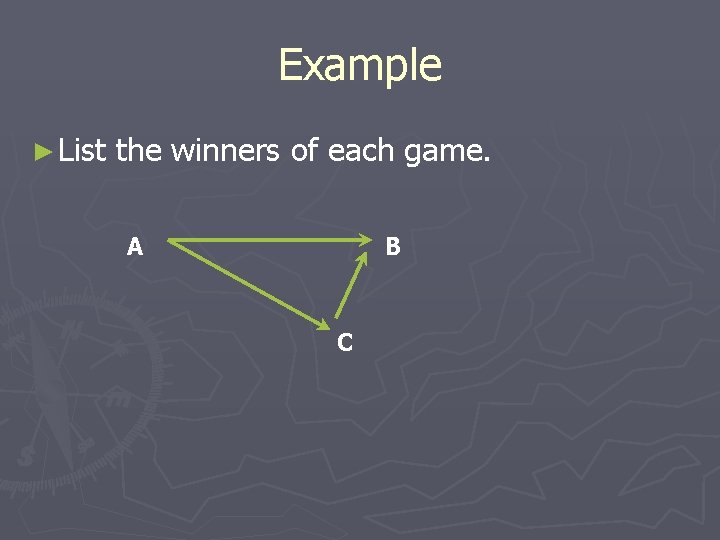
Tournaments ► By using directed edges, we can indicate winners and losers in a tournament. ► An arrow from A to B means that A beats B. ► We use Hamiltonian circuits with digraphs to determine who wins a tournament.

Example ► List the winners of each game. A B C

Why tournaments are cool! ► You can give a ranking for each team if there is exactly one Hamilton path. ► The winners are listed in order of the vertices of your Hamiltonian path.

Example ► Draw a digraph for the following school soccer team round-robin tournament. ► Find the Hamiltonian path and determine the ranking. Game AB AC AD BC BD CD Winner B A D B D D

Example ► Draw a tournament with five players, in which player A defeats everyone, B defeats everyone but A, C is defeated by everyone, and D defeats E.

Find all the directed Hamiltonian paths for the following tournaments. If there is only one, rank the teams. A D B C

Homework p. 205 -206 (5, 8)