Hamilton approch to YangMills Theory in Coulomb Gauge

Hamilton approch to Yang-Mills Theory in Coulomb Gauge H. Reinhardt Tübingen Collaborators: D. Campagnari, D. Epple, C. Feuchter, M. Leder, M. Quandt, W. Schleifenbaum, P. Watson

Plan of the talk • Hamilton approach to continuum Yang-Mills theory in Coulomb gauge • Variational solution of the YM Schrödinger equation: Dyson- Schwinger equations • Numerical Results • Infrared analysis of the DSE • Topological susceptibility • `t Hooft loop • Conclusions

Classical Yang-Mills theory Lagrange function: field strength tensor

Canonical Quantization of Yang-Mills theory Gauß law:

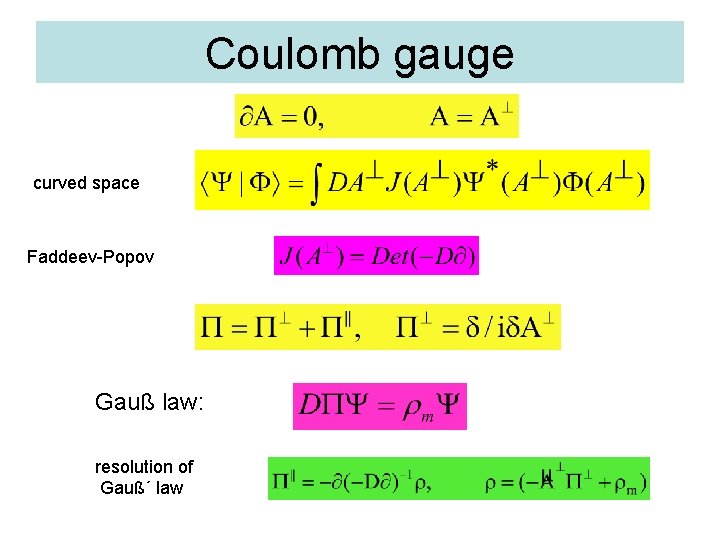
Coulomb gauge curved space Faddeev-Popov Gauß law: resolution of Gauß´ law

YM Hamiltonian in Coulomb gauge Coulomb term Christ and Lee -arises from Gauß´law =neccessary to maintain gauge invariance -provides the confining potential

aim: solving the Yang-Mills Schrödinger eq. for the vacuum by the variational principle with suitable ansätze for metric of the space of gauge orbits: Dyson-Schwinger equations

Importance of the Faddeev-Popov determinant defines the metric in the space of gauge orbits and hence reflects the gauge invariance

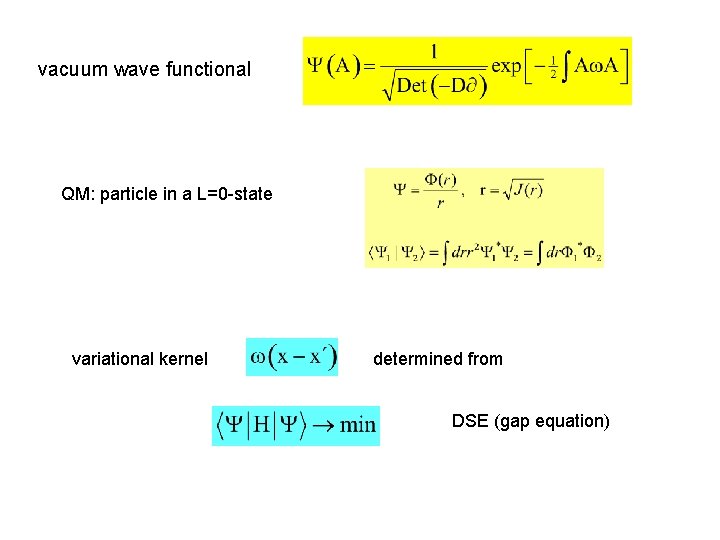
vacuum wave functional QM: particle in a L=0 -state variational kernel determined from DSE (gap equation)

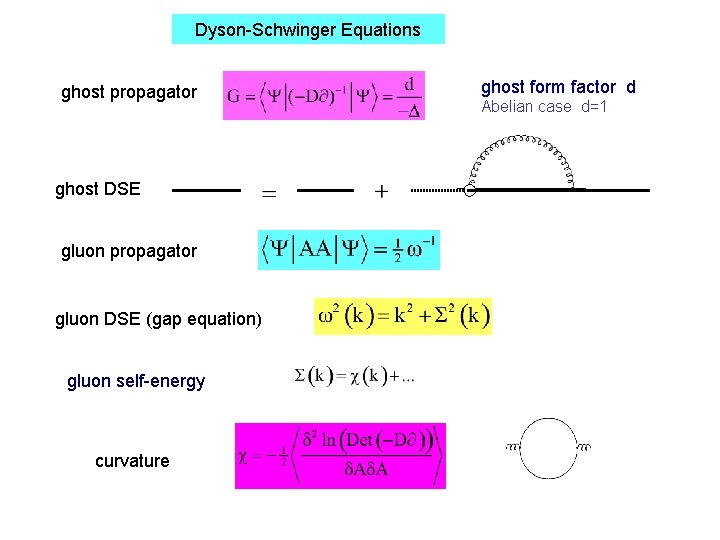
Dyson-Schwinger Equations ghost propagator ghost DSE gluon propagator gluon DSE (gap equation) gluon self-energy curvature ghost form factor d Abelian case d=1

Regularization and renormalization: momentum subtraction scheme renormalization constants: ultrviolet and infrared asymtotic behaviour of the solutions to the Schwinger Dyson equations is independent of the renormalization constants except for horizon condition Zwanziger In D=2+1 is the only value for which the coupled Schwinger-Dyson equation have a self-consistent solution

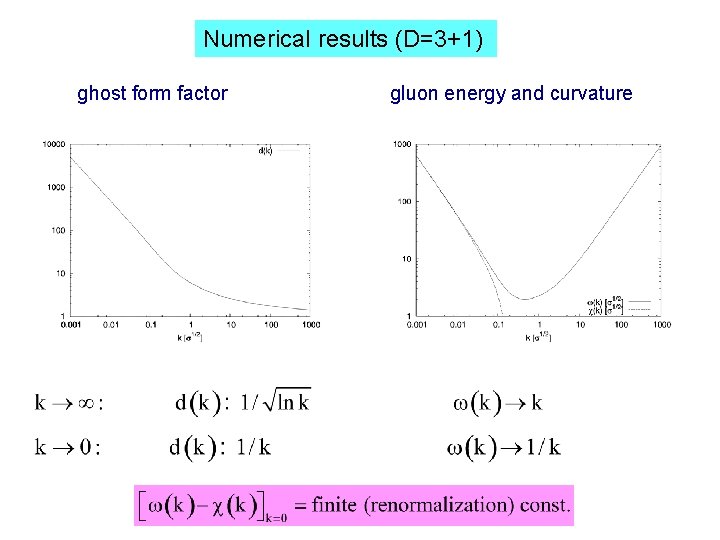
Numerical results (D=3+1) ghost form factor gluon energy and curvature

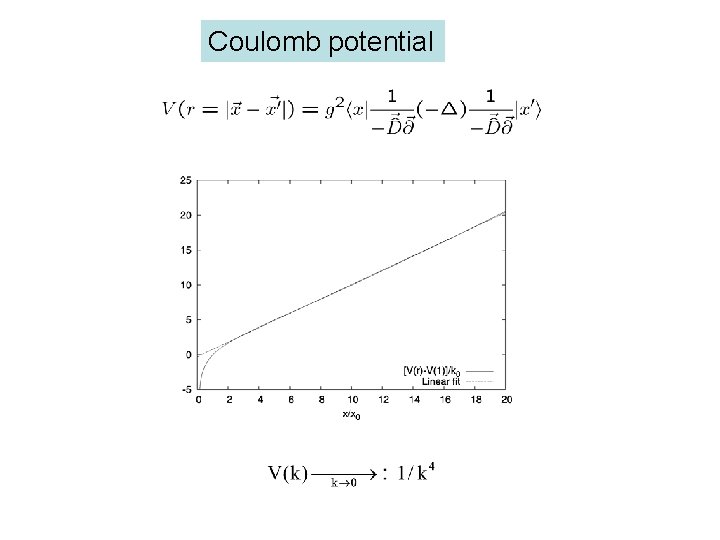
Coulomb potential

Coulomb form factor f Schwinger-Dyson eq. rigorous result to 1 -loop:

external static color sources electric field ghost propagator

The color electric flux tube missing: back reaction of the vacuum to the external sources

The dielectric „constant“ of the Yang-Mills vacuum Maxwell´s displecement dielectric „constant“ k The Yang-Mills vacuum is a perfect color dia-electric

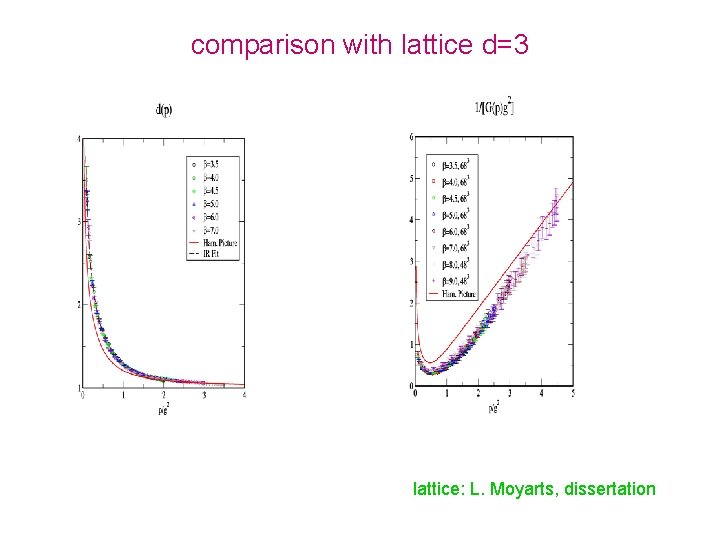
comparison with lattice d=3 lattice: L. Moyarts, dissertation

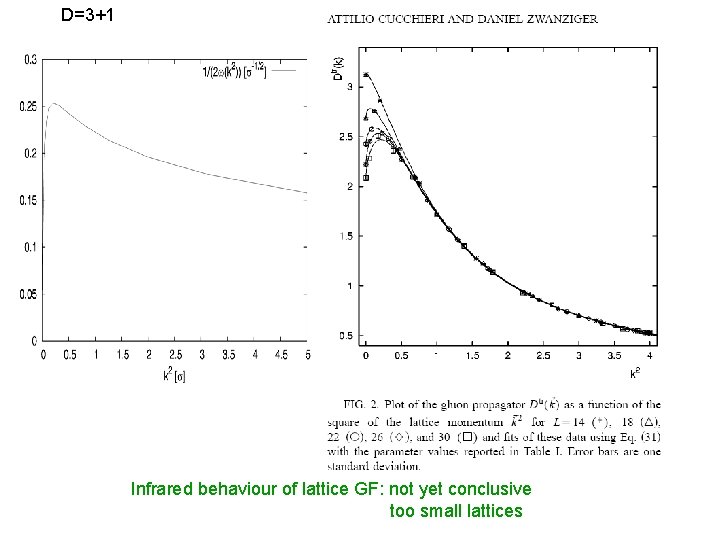
D=3+1 Infrared behaviour of lattice GF: not yet conclusive too small lattices

related work: A. P. Szczepaniak, E. S. Swanson, Phys. Rev. 65 (2002) 025012 A. P. Szczepaniak, Phys. Rev. 69(2004) 074031 different ansatz for the wave functional did not include the curvature of the space of gauge orbits i. e. the Faddeev- Popov determinant present work: C. Feuchter & H. R. hep-th/0402106, PRD 70(2004) hep-th/0408237, PRD 71(2005) W. Schleifenbaum, M. Leder, H. R. PRD 73(2006) D. Epple, H. R. , W. Schleifenbaum, in prepration full inclusion of the curvature measure for the curvature

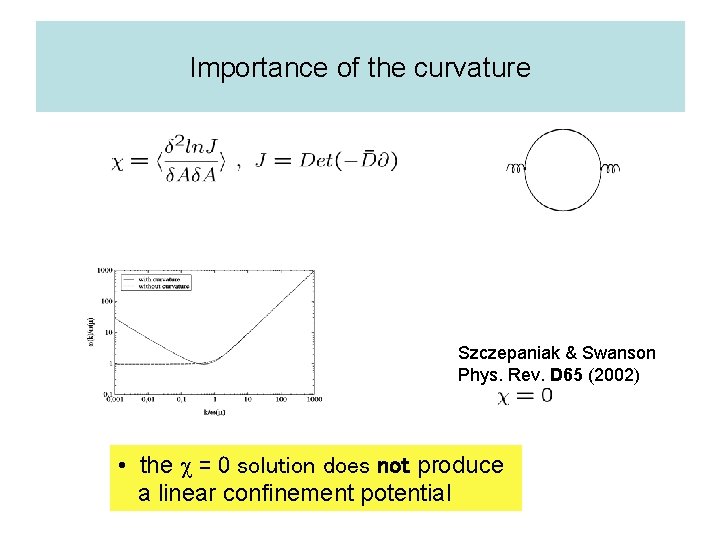
Importance of the curvature Szczepaniak & Swanson Phys. Rev. D 65 (2002) • the c = 0 solution does not produce a linear confinement potential

Robustness of the infrared limit to 2 -loop order: Infrared limit = independent of

Infrared analysis of the DSE vacuum wave functional: generating functional ghost dominance in the infrared d=4 Landau gauge functional integral d=3 Coulomb gauge canonical quantization strong coupling

Analytic solution of DSE in the infrared gluon propagator LG: Lerche, v. Smekal Zwanziger, Alkofer, Fischer, … CG: Schleifenbaum, Leder, H. R. ghost propagator basic assumption: Gribov´s confinment scenario at work horizon condition: ghost DSE (bare ghost-gluon vertex) sum rule: Landau gauge d=4 Coulomb gauge d=3 Coulomb gauge d=2 solution of gluon DSE

running coupling Fischer, Zwanziger interpolating gauges sum rule for the infrared exponents from ghost DSE

Topological susceptibility Witten-Veniciano formula:

Topological susceptibility in Hamilton approach spatial gauge transformation: explicit realization: Chern-Simon action: topological susceptibility: vanishes to all orders in g

Identify our variational wave functional with the restriction of the gauge invarinant to Coulomb gauge exact cancelation of the Abelian part of BB very preliminary result (D. Campagnari -Diploma thesis) (very crude parametrization of the ghost and gluon GFs) : Input: 2 -loop formula for the running coupling

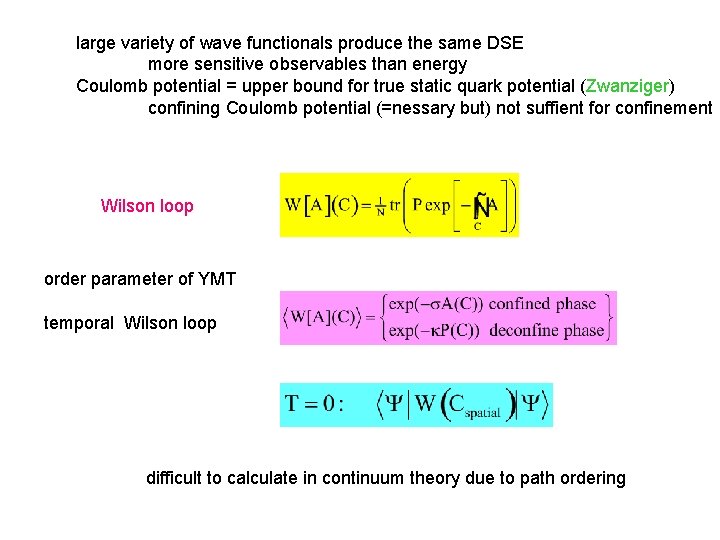
large variety of wave functionals produce the same DSE more sensitive observables than energy Coulomb potential = upper bound for true static quark potential (Zwanziger) confining Coulomb potential (=nessary but) not suffient for confinement Wilson loop order parameter of YMT temporal Wilson loop difficult to calculate in continuum theory due to path ordering

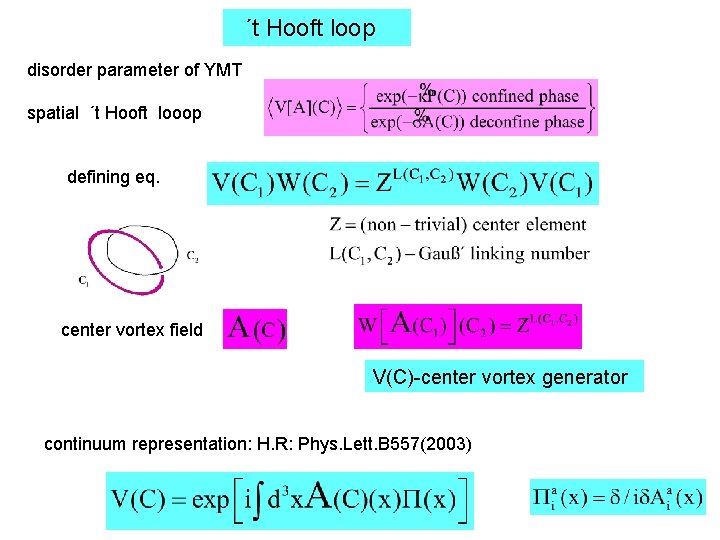
´t Hooft loop disorder parameter of YMT spatial ´t Hooft looop defining eq. center vortex field V(C)-center vortex generator continuum representation: H. R: Phys. Lett. B 557(2003)

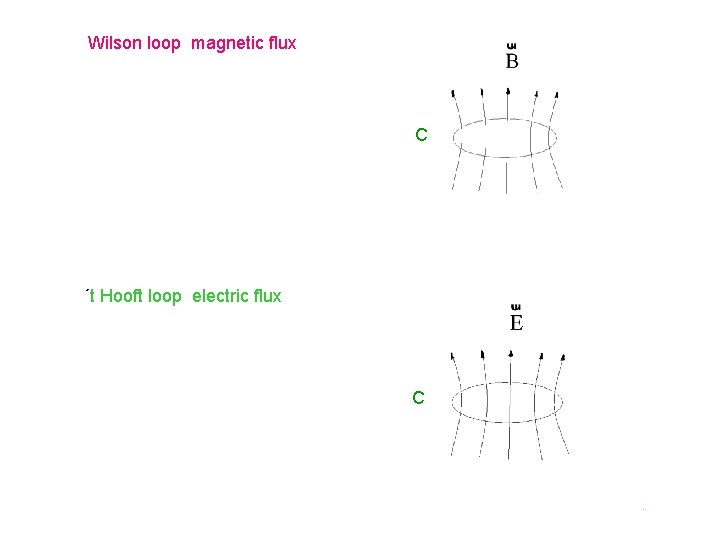
Wilson loop magnetic flux C ´t Hooft loop electric flux C

QM: wave functionals in Coulomb gauge satisfy Gauß´law and hence should be regarded as the gauge invariant wave functional restricted to transverse gauge fields.

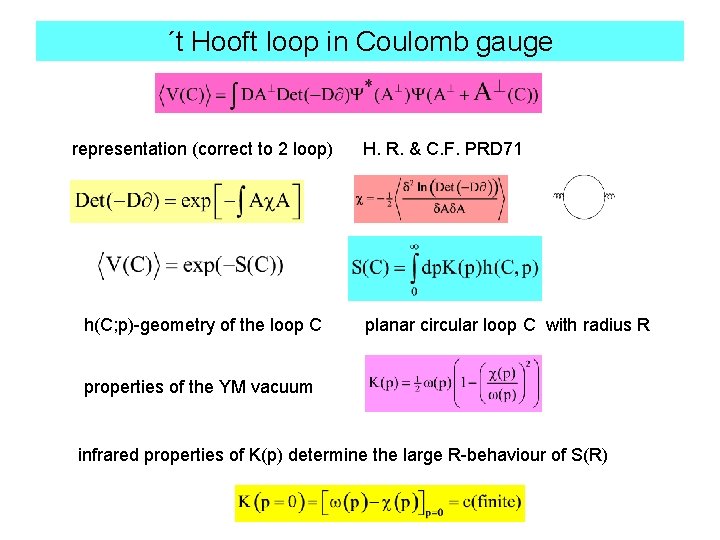
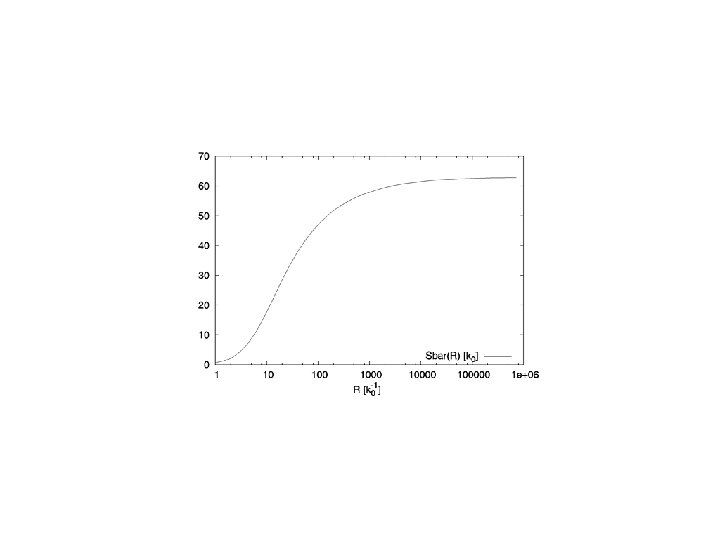
´t Hooft loop in Coulomb gauge representation (correct to 2 loop) h(C; p)-geometry of the loop C H. R. & C. F. PRD 71 planar circular loop C with radius R properties of the YM vacuum infrared properties of K(p) determine the large R-behaviour of S(R)

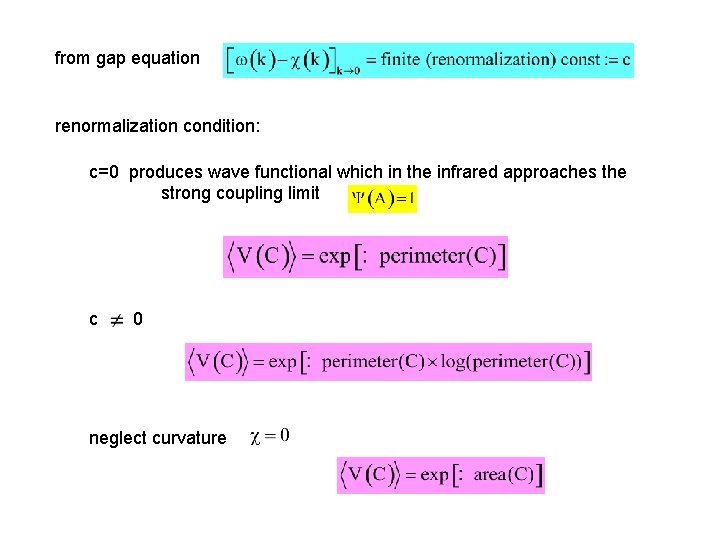
from gap equation renormalization condition: c=0 produces wave functional which in the infrared approaches the strong coupling limit c 0 neglect curvature

Summary and Conclusion • Variational solution of the YM Schrödinger equation in Coulomb gauge • Quark and gluon confinement • IR-finite running coupling • Curvature in gauge orbit space (Fadeev –Popov determinant) is crucial for the confinement properties • Topological susceptibility • ´t Hooft loop: perimeter law for a wave functional which in the infrared shows strict ghost dominance

Thanks to the organizers