Half Adder Full Adder Patrick Marshall Intro Adding

Half Adder & Full Adder Patrick Marshall

Intro • • • Adding binary digits Half adder Full adder Parallel adder (ripple carry) Arithmetic overflow

Adding Binary Numbers 10110 - 22 00110 - 6 11100 - 28 A key requirement of digital computers is the ability to use logical functions to perform arithmetic operations. How do we add two binary numbers? Let's start by adding two binary bits. Since each bit has only two possible values, 0 or 1, there are only four possible combinations of inputs. These four possibilities, and the resulting sums, are: 0+0=0 0+1=1 1+0=1 1 + 1 = 10

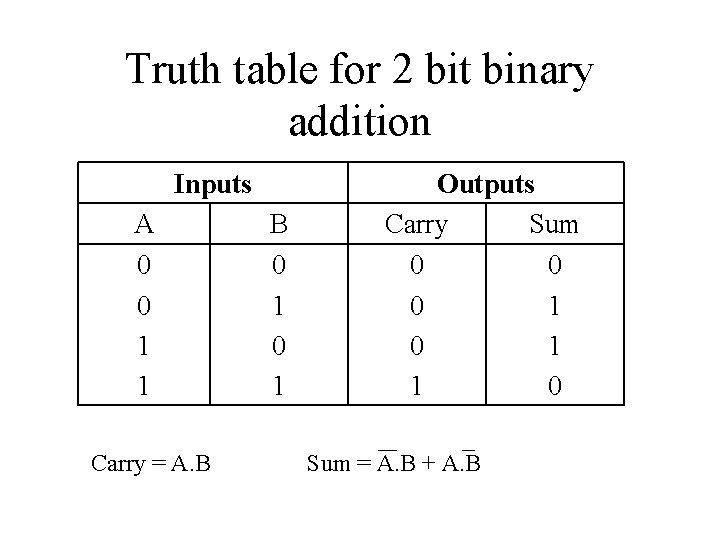
Truth table for 2 bit binary addition Inputs A 0 0 1 1 Carry = A. B B 0 1 Outputs Carry Sum 0 0 0 1 1 0 Sum = A. B + A. B

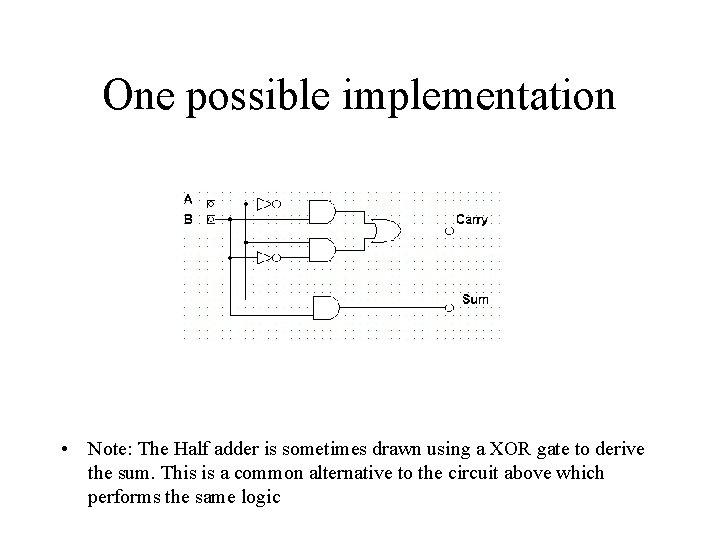
One possible implementation • Note: The Half adder is sometimes drawn using a XOR gate to derive the sum. This is a common alternative to the circuit above which performs the same logic

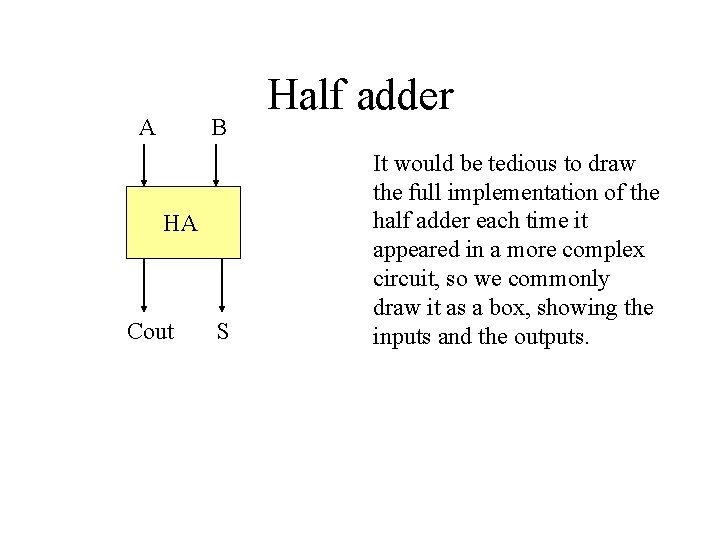
A B HA Cout S Half adder It would be tedious to draw the full implementation of the half adder each time it appeared in a more complex circuit, so we commonly draw it as a box, showing the inputs and the outputs.

Adding groups of digits 10110 = 22 00110 = 6 11100 = 28 decimal 0+0+0=0 1+0+0=1 decimal 1 + 0 = 10 1 + 1 = 11 In digital circuits we usually have to add groups of bits together, rather than simply one bit to one bit as shown in the half adder. If multiple bit number representations, like 100110 are to be added to 00110 for each digit additions we must take into account carry bits from previous steps of the process. In other words we need a circuit which will do the full job of multiple bit binary addition. The half adder is so called because it performs ‘half’ the job of binary addition.

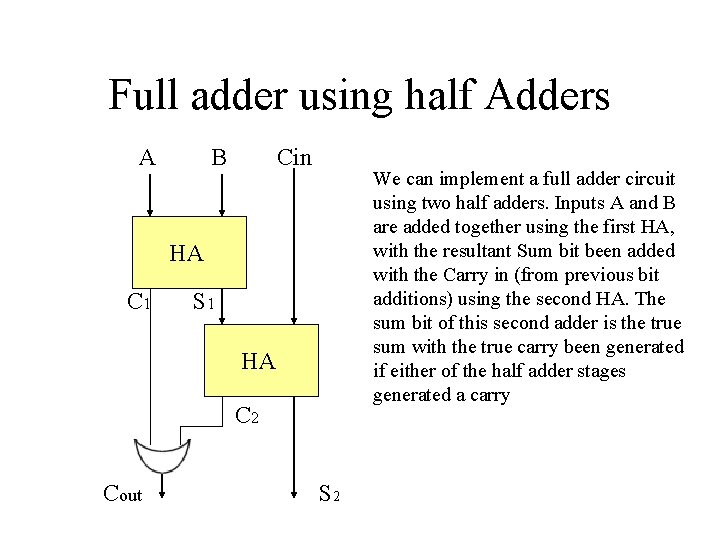
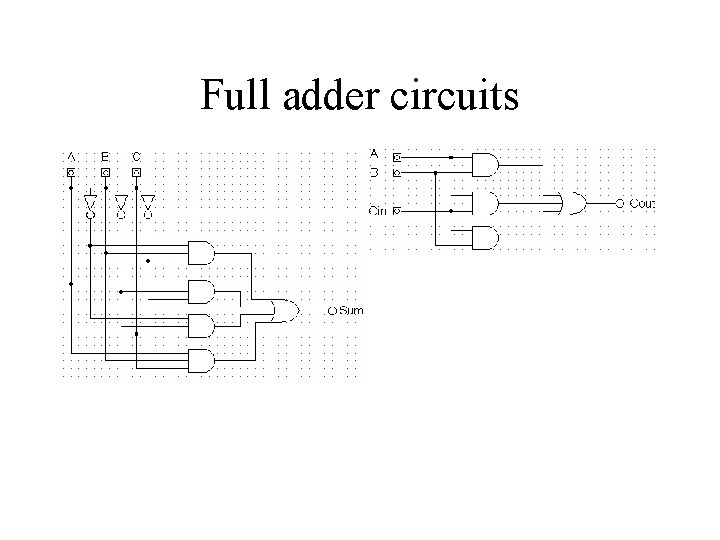
Full adder using half Adders A B Cin We can implement a full adder circuit using two half adders. Inputs A and B are added together using the first HA, with the resultant Sum bit been added with the Carry in (from previous bit additions) using the second HA. The sum bit of this second adder is the true sum with the true carry been generated if either of the half adder stages generated a carry HA C 1 S 1 HA C 2 Cout S 2

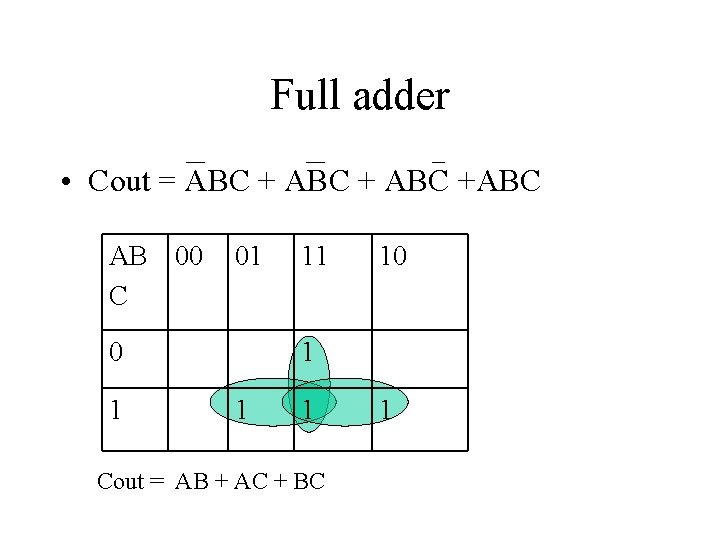
Implementing the Full adder circuit A B Cin Sum Cout 0 0 1 1 0 1 0 1 0 1 1 0 0 1 1 0 0 0 1 1 1 Sum = ABC + ABC Cout = ABC +ABC This adder can be considered a three input adder. Two inputs, A&B, from the bits of the numbers we are adding and one bit, Cin, is from additions of previous bits

Full adder • Cout = ABC +ABC AB 00 C 01 0 1 11 10 1 1 1 Cout = AB + AC + BC 1

Full adder circuits

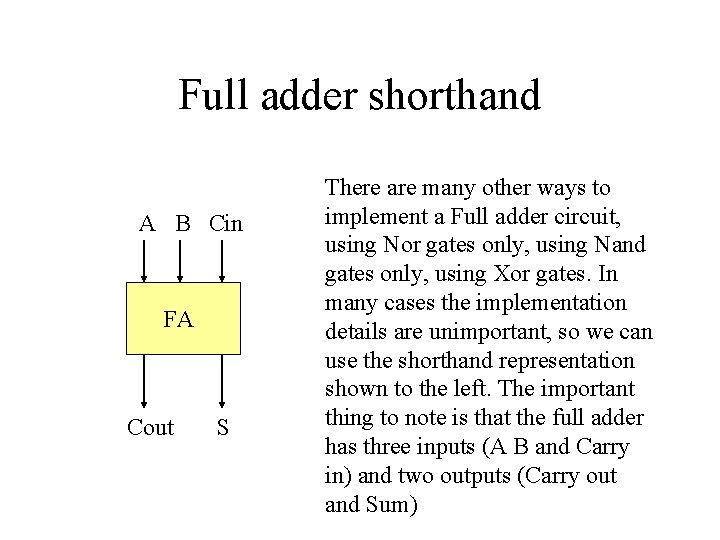
Full adder shorthand A B Cin FA Cout S There are many other ways to implement a Full adder circuit, using Nor gates only, using Nand gates only, using Xor gates. In many cases the implementation details are unimportant, so we can use the shorthand representation shown to the left. The important thing to note is that the full adder has three inputs (A B and Carry in) and two outputs (Carry out and Sum)

Adding mulitple bits • We have seen how to add two binary digits using the half adder, we have seen how to add two binary digits and a carry digit from a previous stage using the full adder. These operations are not terribly useful as generally we need to add large numbers together which are represented by multiple binary digits. • We will now look at a way to achieve this using a parallel full adder.

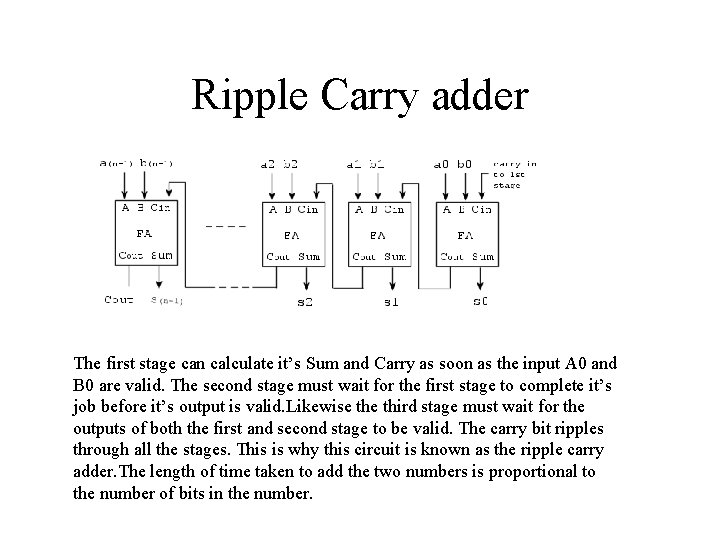
Parallel Full Adder • A parrallel adder adds all the bits the binary numbers in a single operation. • One such adder is known as the ripple carry adder

Ripple Carry adder The first stage can calculate it’s Sum and Carry as soon as the input A 0 and B 0 are valid. The second stage must wait for the first stage to complete it’s job before it’s output is valid. Likewise third stage must wait for the outputs of both the first and second stage to be valid. The carry bit ripples through all the stages. This is why this circuit is known as the ripple carry adder. The length of time taken to add the two numbers is proportional to the number of bits in the number.

Notes on Ripple Carry adder Setting the “Carry in to 1 st Stage” to a ‘ 1’ to generate A+B+1. If input B were zero the circuit would function as an incrementor. This also is handy when applying complimentary arithmetic. The Carry out bit can be used to determine if arithmetic overflow has occurred. Overflow occurs when the resulting value of an operation performed on valid representations of numbers is out of the range of valid values. That is, the resulting value is greater than max or less than min. It is possible to reduce partially the effect of the ripple-through carry by creating what are called “carry look ahead circuits”. That is the carry out to stage 5 can be calculated by inspecting the inputs to 4, 3, 2 and 1. This high speed circuit avoids the delays experience if a ripple through carry circuit.

Arithmetic overflow • Consider 4 bit two’s complement additions, so the valid decimal range is from – 8 to +7 0100 = 4 1100 = -4 0111 = 7 1000 = -8 +0010 = 2 +1110 = -2 +0011 = 3 +1100 = -4 0110 = 6 11110 = -2 1010 = -6 10100 = +4 The first two sum are fine, but there’s something funny with 7 + 3 = -6 and – 8 – 4 = +4

Arithmetic Overflow • Overflow occurs if the result of adding two positive numbers yields a negative result or if the adding of two negative numbers result in a positive result. If the sign bits of the two numbers are the same but the sign bit of the result is different then arithmetic overflow has occurred. Overflow (V) = A sign. B sign. Sum sign or A sign. B sign. Sum sign

Summary • • • Adding binary digits Half adder Full adder Parallel adder (ripple carry) Arithmetic overflow