Hadron structure with electromagnetic probes Marc Vanderhaeghen Johannes

Hadron structure with electromagnetic probes Marc Vanderhaeghen Johannes Gutenberg Universität, Mainz Graduate School HANUC Jyväskylä, August 25 -29, 2008

nucleon form factors (generalized) parton distributions spin, tomography excitation spectrum Δ(1232), …

Outline lectures Ia. Introduction : some “key” questions in hadron structure physics Ib. Nucleon electromagnetic form factors, two-photon exchange, quark transverse charge densities II. Generalized Parton Distributions (GPDs) III. Nucleon excitation spectrum, chiral EFT in the Δ(1232) region, and time-like processes

Strong QCD : from quarks to hadrons nucleon : many body system of quarks, anti-quarks, gluons quarks come in 3 color charges dynamics : non-abelian gauge theory ( QCD ) ’independent’ nucleon motion in nuclei ( BE ≈ 1 % ) collective nuclear behavior QCD phase diagram : quark -gluon plasma

Ia. Some “key” questions in hadron structure research 1) Why can quarks not be isolated (confinement) ? 2) How can we ‘see’ quarks (quark-gluon structure) ? 3) What is the origin of the mass of the hadrons ? 4) Which symmetries govern hadron structure ? Role of effective degrees of freedom : (pion cloud, constituent quarks, flux tube, …)

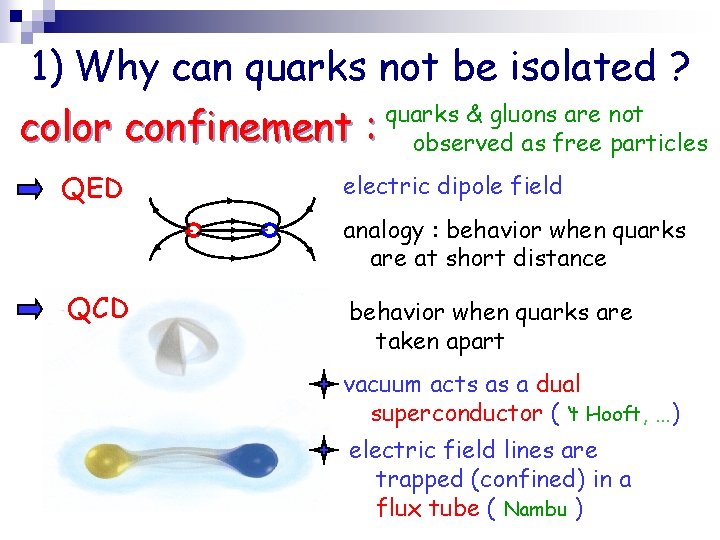
1) Why can quarks not be isolated ? quarks & gluons are not color confinement : observed as free particles QED electric dipole field + QCD - analogy : behavior when quarks are at short distance behavior when quarks are taken apart vacuum acts as a dual superconductor ( ‘t Hooft, …) electric field lines are trapped (confined) in a flux tube ( Nambu )

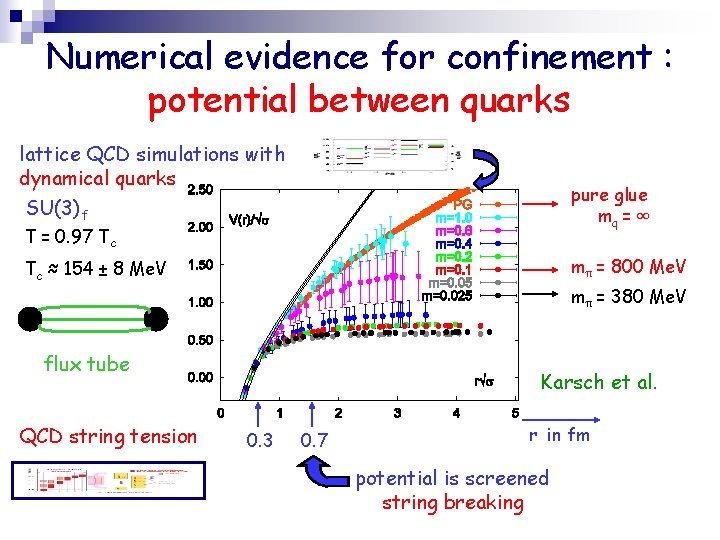
Numerical evidence for confinement : potential between quarks lattice QCD simulations with dynamical quarks SU(3)f pure glue mq = ∞ T = 0. 97 Tc mπ = 800 Me. V Tc ≈ 154 ± 8 Me. V mπ = 380 Me. V flux tube QCD string tension Karsch et al. 0. 3 0. 7 r in fm potential is screened string breaking

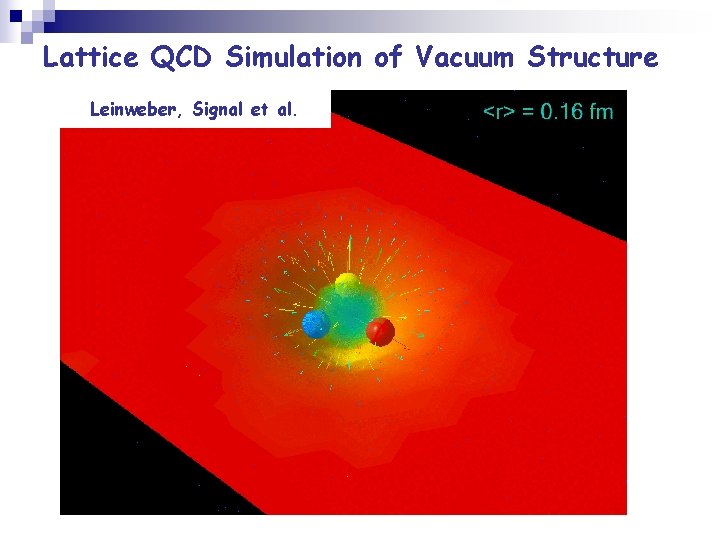
Lattice QCD Simulation of Vacuum Structure Leinweber, Signal et al.

2) How can one ‘see’ quarks ?

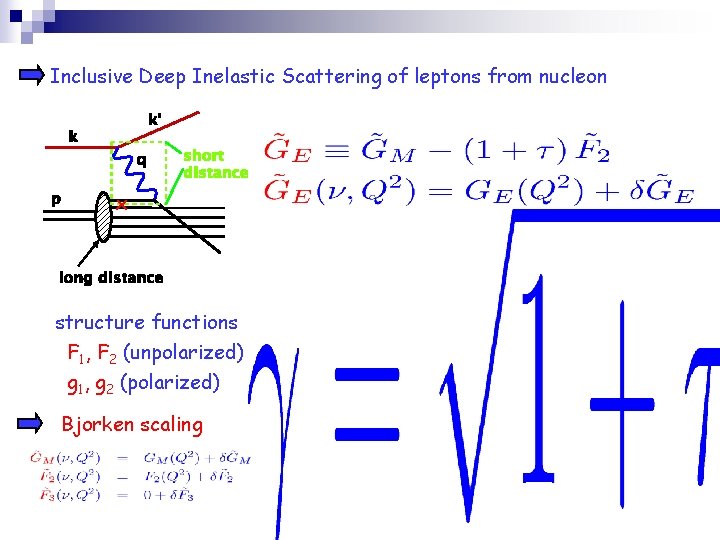
Inclusive Deep Inelastic Scattering of leptons from nucleon x structure functions F 1, F 2 (unpolarized) g 1, g 2 (polarized) Bjorken scaling

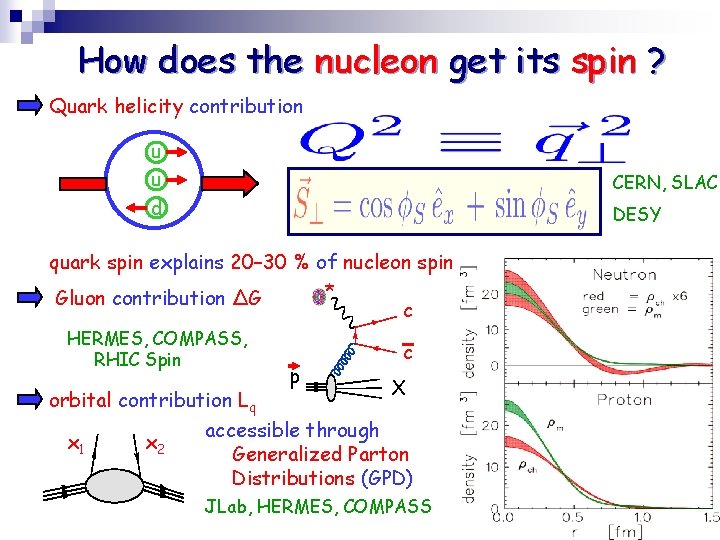
How does the nucleon get its spin ? Quark helicity contribution u u d CERN, SLAC, DESY quark spin explains 20– 30 % of nucleon spin * Gluon contribution ΔG HERMES, COMPASS, RHIC Spin p c c X orbital contribution Lq accessible through x 1 x 2 Generalized Parton Distributions (GPD) JLab, HERMES, COMPASS

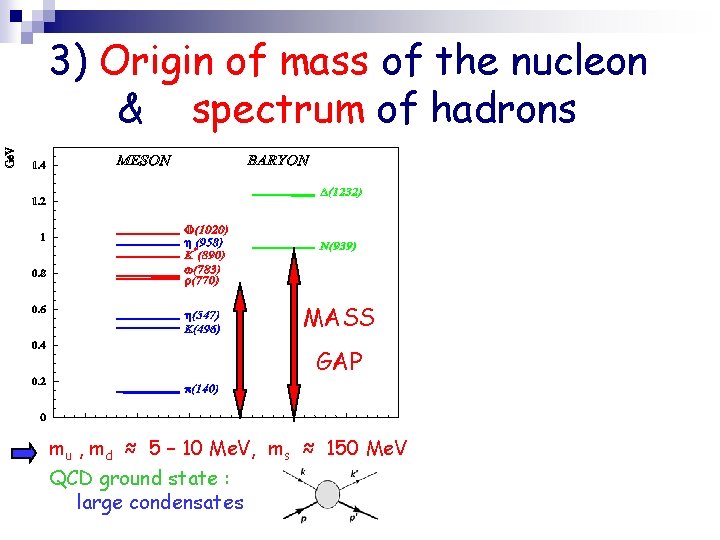
3) Origin of mass of the nucleon & spectrum of hadrons MASS GAP mu , md ≈ 5 – 10 Me. V, ms ≈ 150 Me. V QCD ground state : large condensates

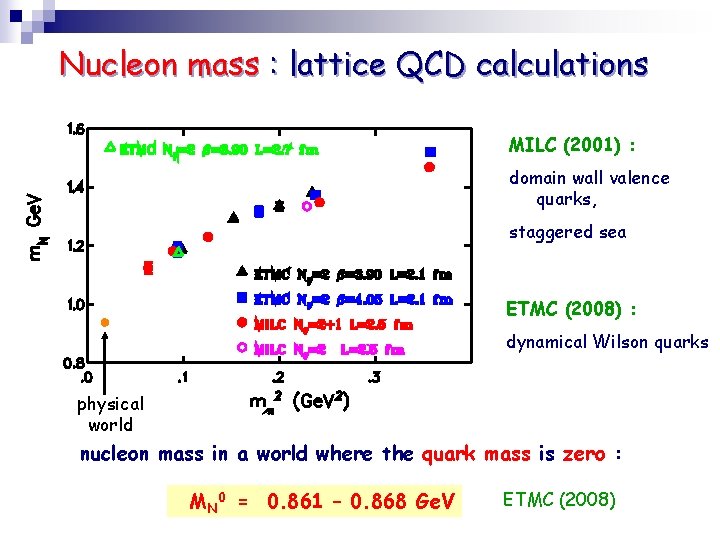
Nucleon mass : lattice QCD calculations MILC (2001) : domain wall valence quarks, staggered sea ETMC (2008) : dynamical Wilson quarks physical world nucleon mass in a world where the quark mass is zero : MN 0 = 0. 861 – 0. 868 Ge. V ETMC (2008)

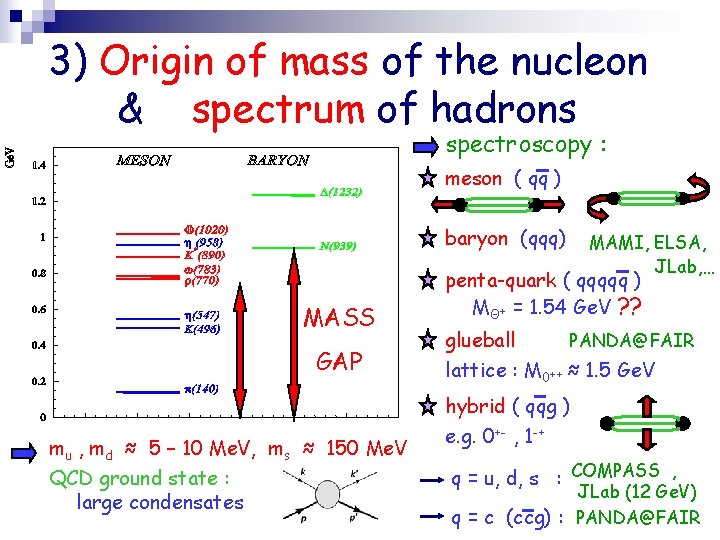
3) Origin of mass of the nucleon & spectrum of hadrons spectroscopy : meson ( qq ) baryon (qqq) MASS GAP mu , md ≈ 5 – 10 Me. V, ms ≈ 150 Me. V QCD ground state : large condensates MAMI, ELSA, JLab, … penta-quark ( qqqqq ) MΘ+ = 1. 54 Ge. V ? ? glueball PANDA@FAIR lattice : M 0++ ≈ 1. 5 Ge. V hybrid ( qqg ) e. g. 0+- , 1 -+ q = u, d, s : COMPASS , JLab (12 Ge. V) q = c (ccg) : PANDA@FAIR

QCD: Exotics QCD predicts the existence of exotic mesons Glueballs are mesons without valence quarks “pure gluon” states emblematic of non-Abelian nature of QCD (lattice QCD predicts mass for 0++ around 1. 5 Ge. V) Other exotics involve excitation or vibration of gluons

Glueballs n n Glueballs are “pure gluon” states emblematic of non. Abelian nature of QCD Aim to compute masses of lowest few states of given quantum number Morningstar and Peardon PRD 60, 034509 lattice glueball calculations provide road-map (N. B. r 0 -1 ~ 0. 4 Ge. V)

Exotics : BNL / GSI (PANDA@FAIR) / JLab (Hall D) n n n Computations in heavy-quark sector- insight into excitations of the string For heavy quarks, energy associated with “excited string” of around 1 Ge. V Lowest 1 -+ state around 1. 8 -2. 0 Ge. V

Glueballs and hybrid mesons

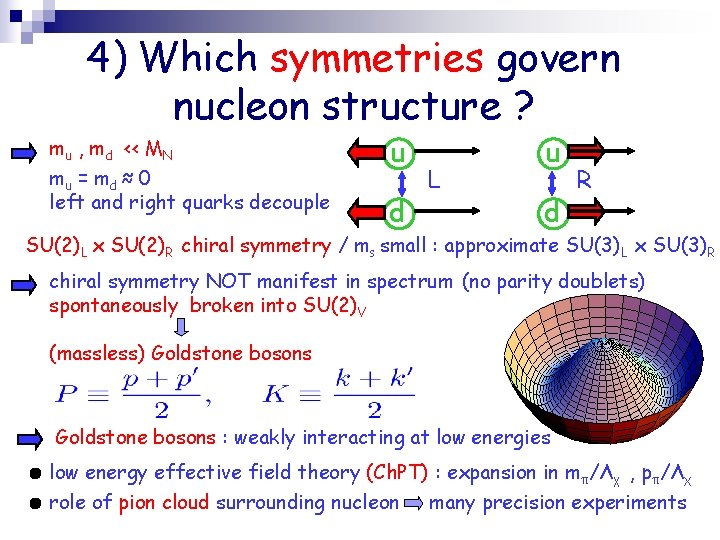
4) Which symmetries govern nucleon structure ? mu , md << MN mu = md ≈ 0 left and right quarks decouple u d L u d R SU(2)L x SU(2)R chiral symmetry / ms small : approximate SU(3)L x SU(3)R chiral symmetry NOT manifest in spectrum (no parity doublets) spontaneously broken into SU(2)V (massless) Goldstone bosons : weakly interacting at low energies low energy effective field theory (Ch. PT) : expansion in mπ/Λχ , pπ/Λχ role of pion cloud surrounding nucleon many precision experiments

Ib. Nucleon e. m. form factors, two-photon exchange and quark charge densities data : nucleon e. m. form factors two-photon exchange processes lattice QCD calculations for nucleon FFs quark transverse charge densities from nucleon e. m. FFs and deuteron e. m. FFs

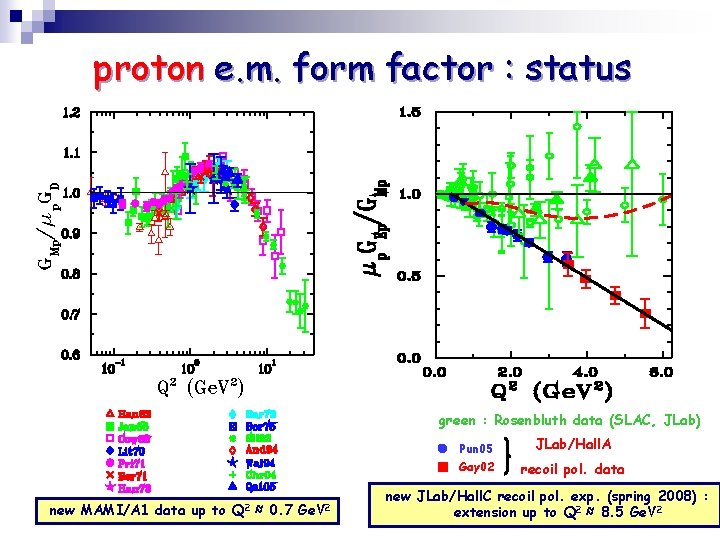
proton e. m. form factor : status green : Rosenbluth data (SLAC, JLab) new MAMI/A 1 data up to Q 2 ≈ 0. 7 Ge. V 2 Pun 05 JLab/Hall. A Gay 02 recoil pol. data new JLab/Hall. C recoil pol. exp. (spring 2008) : extension up to Q 2 ≈ 8. 5 Ge. V 2

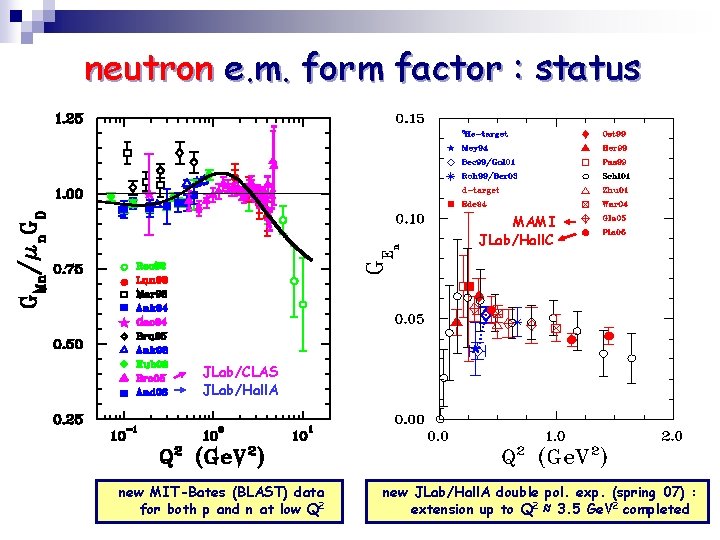
neutron e. m. form factor : status MAMI JLab/Hall. C JLab/CLAS JLab/Hall. A new MIT-Bates (BLAST) data for both p and n at low Q 2 new JLab/Hall. A double pol. exp. (spring 07) : extension up to Q 2 ≈ 3. 5 Ge. V 2 completed

neutron GE at larger Q 2 new JLab/Hall. A double pol. exp. E 02 -013 : preliminary results at Q 2 ≈ 1. 7 and 3. 5 Ge. V 2

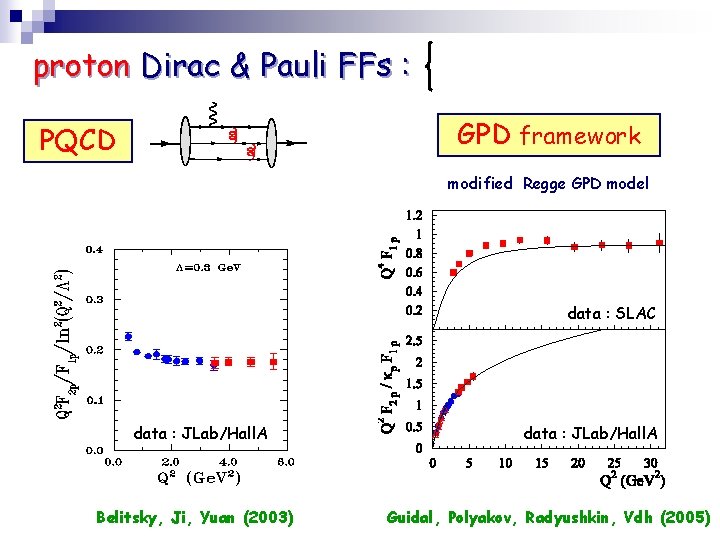
proton Dirac & Pauli FFs : GPD framework PQCD modified Regge GPD model data : SLAC data : JLab/Hall. A Belitsky, Ji, Yuan (2003) data : JLab/Hall. A Guidal, Polyakov, Radyushkin, Vdh (2005)

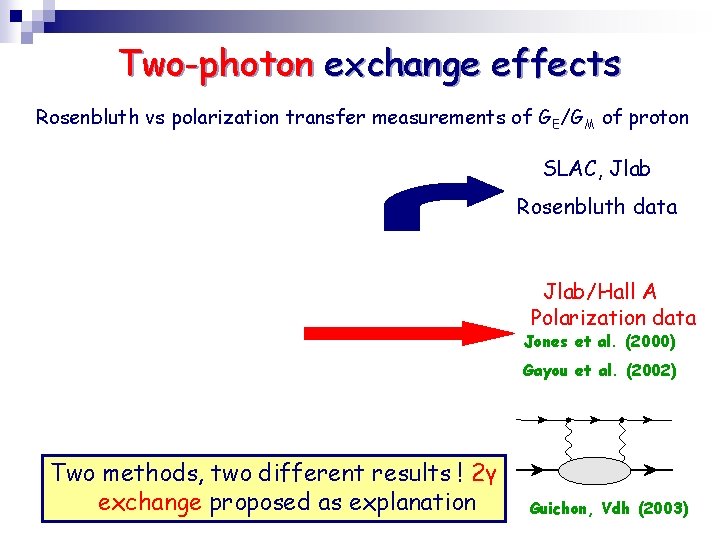
Two-photon exchange effects Rosenbluth vs polarization transfer measurements of GE/GM of proton SLAC, Jlab Rosenbluth data Jlab/Hall A Polarization data Jones et al. (2000) Gayou et al. (2002) Two methods, two different results ! 2γ exchange proposed as explanation Guichon, Vdh (2003)

Elastic e. N scattering beyond one-photon exchange approximation Kinematical invariants : (me = 0) equivalently, introduce

Observables including two-photon exchange Real parts of two-photon amplitudes

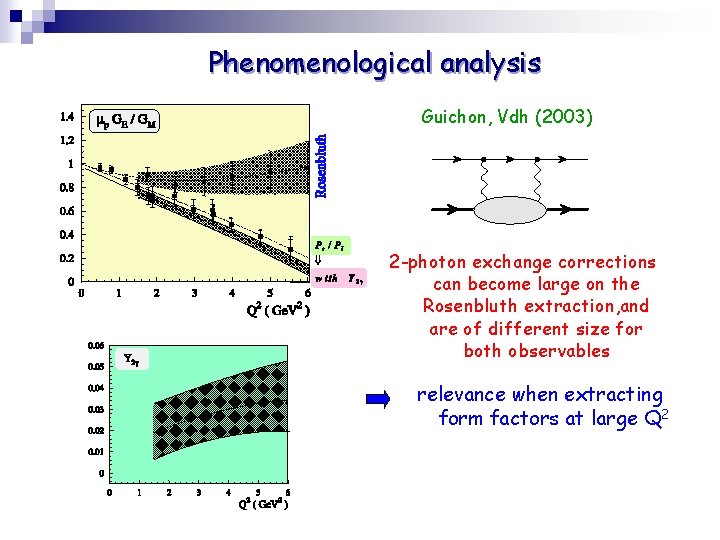
Phenomenological analysis Guichon, Vdh (2003) 2 -photon exchange corrections can become large on the Rosenbluth extraction, and are of different size for both observables relevance when extracting form factors at large Q 2

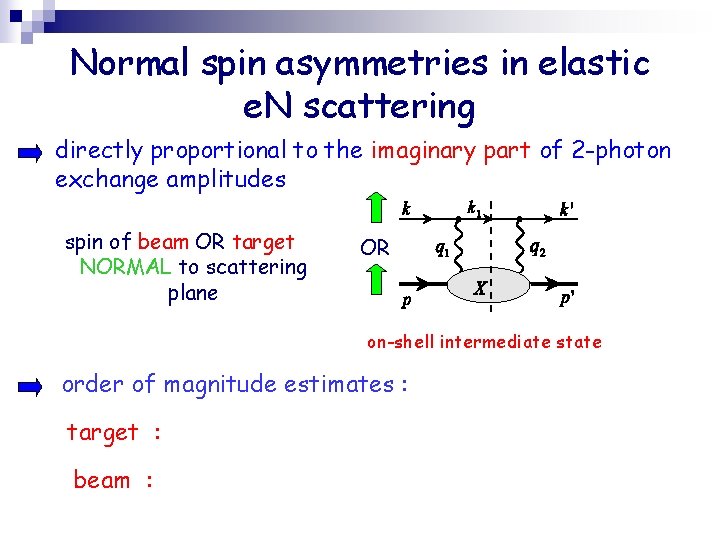
Normal spin asymmetries in elastic e. N scattering directly proportional to the imaginary part of 2 -photon exchange amplitudes spin of beam OR target NORMAL to scattering plane OR on-shell intermediate state order of magnitude estimates : target : beam :

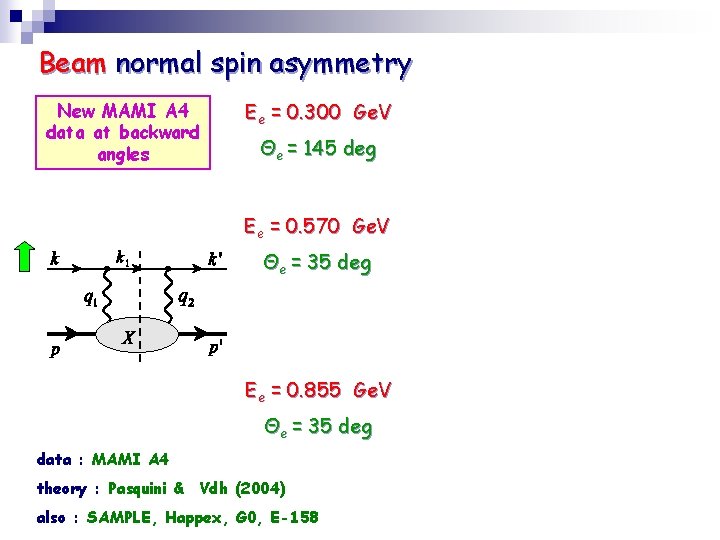
Beam normal spin asymmetry New MAMI A 4 data at backward angles Ee = 0. 300 Ge. V Θe = 145 deg Ee = 0. 570 Ge. V Θe = 35 deg Ee = 0. 855 Ge. V Θe = 35 deg data : MAMI A 4 theory : Pasquini & Vdh (2004) also : SAMPLE, Happex, G 0, E-158

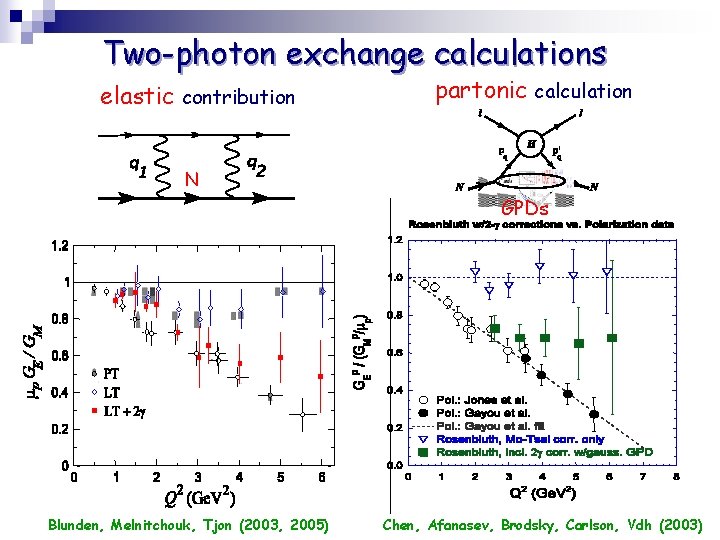
Two-photon exchange calculations elastic contribution partonic calculation N GPDs Blunden, Melnitchouk, Tjon (2003, 2005) Chen, Afanasev, Brodsky, Carlson, Vdh (2003)

whether two-photon exchange is entirely responsible for the discrepancy in the FF extraction is to be determined experimentally Real part of Y 2γ 1) ε-independence of GEp/GMp in recoil polarization 2) cross section difference in e+ and e- proton scattering 3) non-linearity of Rosenbluth plot Also imaginary part 4) from induced out-of-plane polarization 5) single-spin target asymmetry Hall C 04 -019, completed Hall B 07 -005; Olympus/Doris with refurbished BLAST detector Hall C 05 -017; being analyzed by-product of 04 -019/04 -108? Hall A 05 -015 (3 He )

test of ε-dependence of Pt / Pl new JLab/Hall C data (2008) PR to ELIM be qu INAR ote d Y, no t 1γ result for Pt / Pl The preliminary data for Q 2=2. 5 Ge. V 2 show no ε-dependence of GEp/GMp at the 0. 01 level

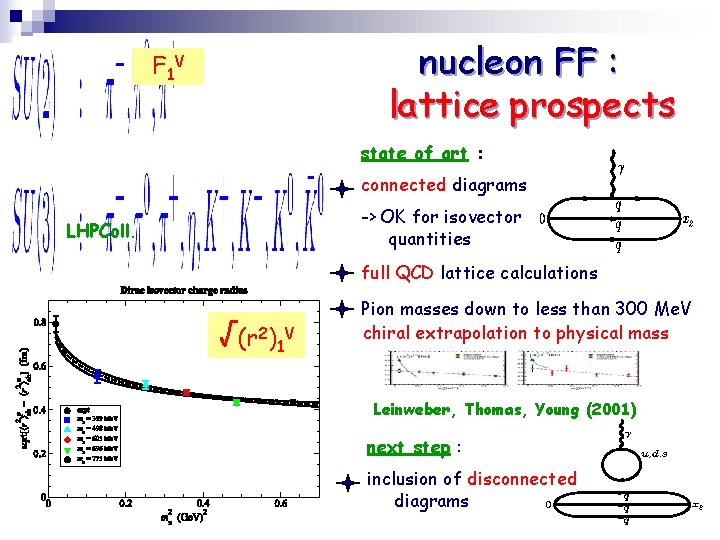
nucleon FF : lattice prospects F 1 V state of art : connected diagrams -> OK for isovector quantities LHPColl. full QCD lattice calculations √(r 2)1 V Pion masses down to less than 300 Me. V chiral extrapolation to physical mass Leinweber, Thomas, Young (2001) next step : inclusion of disconnected diagrams

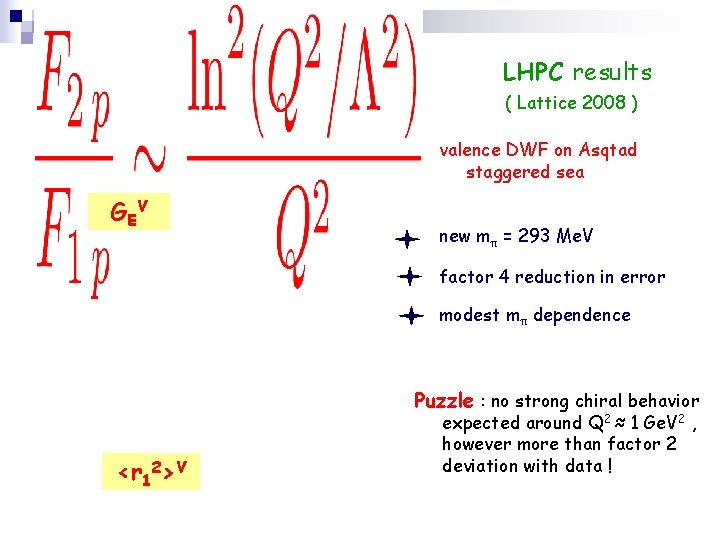
LHPC results ( Lattice 2008 ) valence DWF on Asqtad staggered sea G EV new mπ = 293 Me. V factor 4 reduction in error modest mπ dependence Puzzle : no strong chiral behavior <r 12>V expected around Q 2 ≈ 1 Ge. V 2 , however more than factor 2 deviation with data !

RBC results mπ = 0. 330 Ge. V ( Lattice 2008 ) mπ = 0. 420 Ge. V Nf = 2 + 1 degenerate dynamical flavors of DWF mπ = 0. 560 Ge. V F 1 V mπ = 0. 670 Ge. V F 2 V

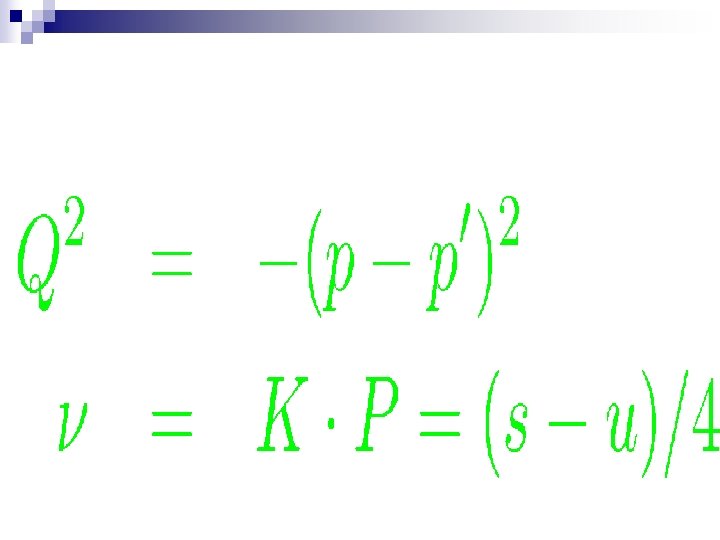
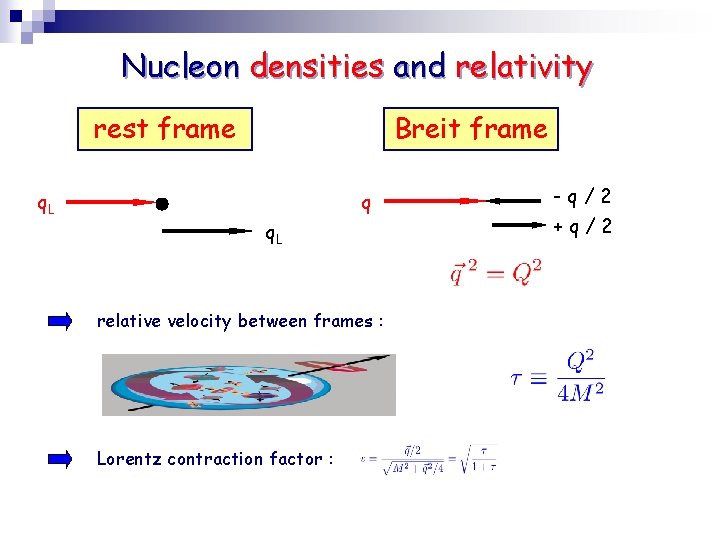
Nucleon densities and relativity rest frame q. L Breit frame q q. L relative velocity between frames : Lorentz contraction factor : -q/2 +q/2

Nucleon densities and relativity rest frame density intrinsic FF non-rel : importance of relativity limit : k = 2 M (Compton wavelength) Kelly (2000)

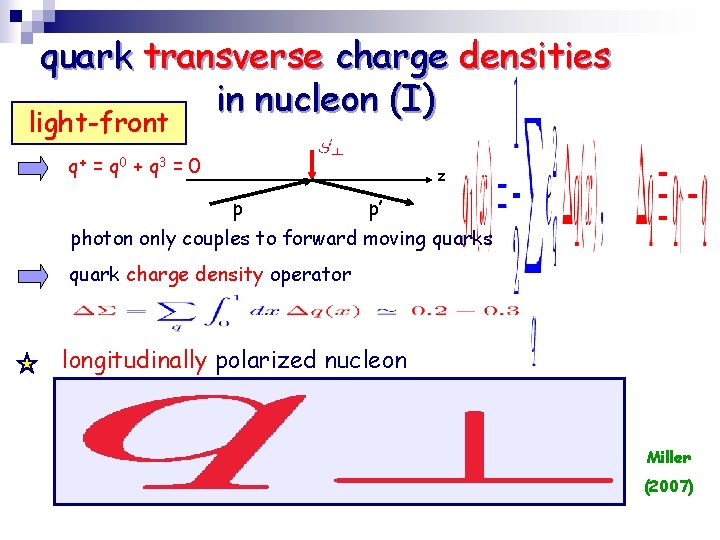
quark transverse charge densities in nucleon (I) light-front q+ = q 0 + q 3 = 0 z p p’ photon only couples to forward moving quarks quark charge density operator longitudinally polarized nucleon Miller (2007)

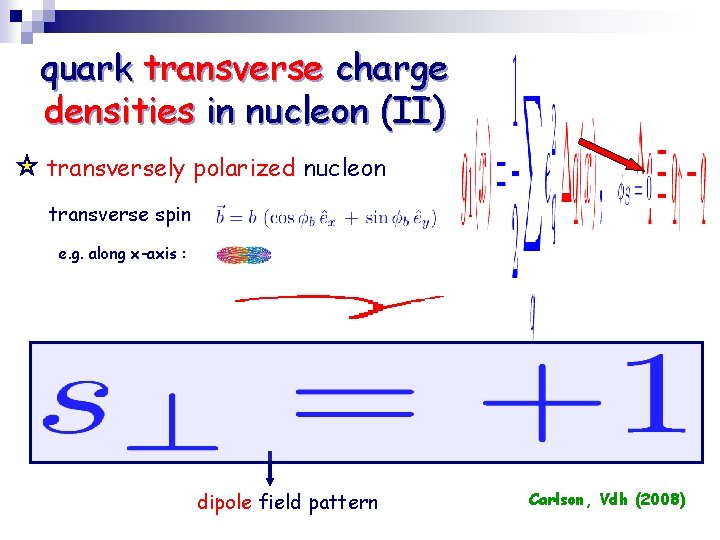
quark transverse charge densities in nucleon (II) transversely polarized nucleon transverse spin e. g. along x-axis : dipole field pattern Carlson, Vdh (2008)

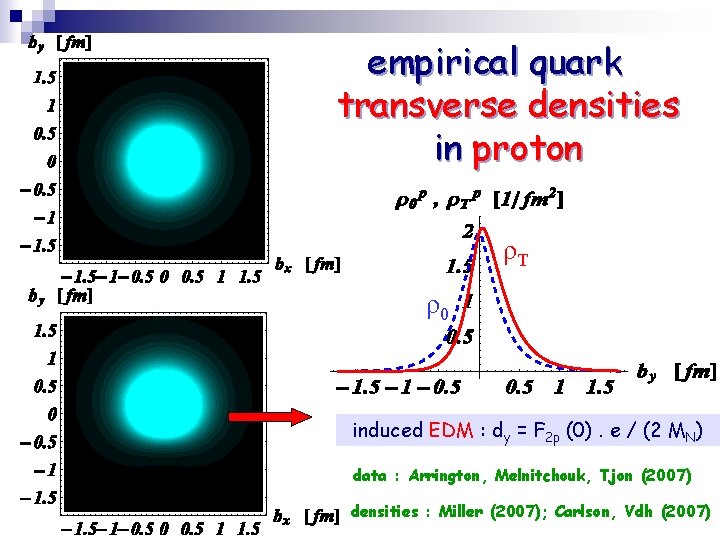
empirical quark transverse densities in proton ρT ρ0 induced EDM : dy = F 2 p (0). e / (2 MN) data : Arrington, Melnitchouk, Tjon (2007) densities : Miller (2007); Carlson, Vdh (2007)

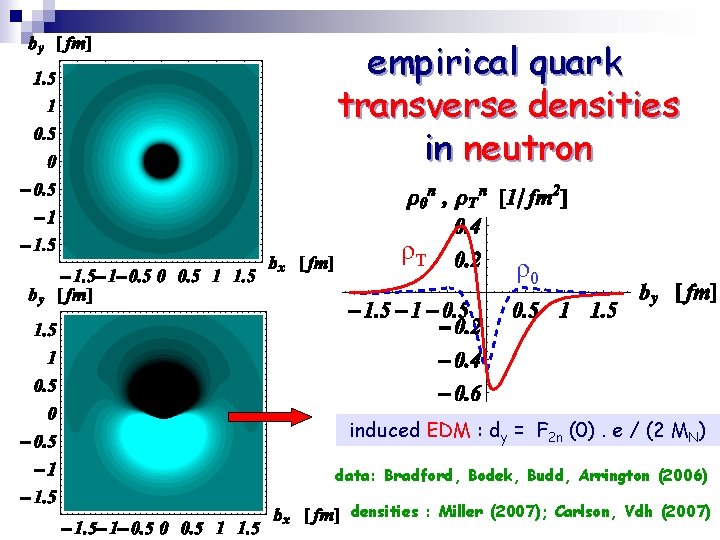
empirical quark transverse densities in neutron ρT ρ0 induced EDM : dy = F 2 n (0). e / (2 MN) data: Bradford, Bodek, Budd, Arrington (2006) densities : Miller (2007); Carlson, Vdh (2007)

empirical quark transverse densities in deuteron λ= ± 1 λ= 0 separated data up to 2 Ge. V 2 : Abbott et al. (2000) densities : Carlson, Vdh (2008)

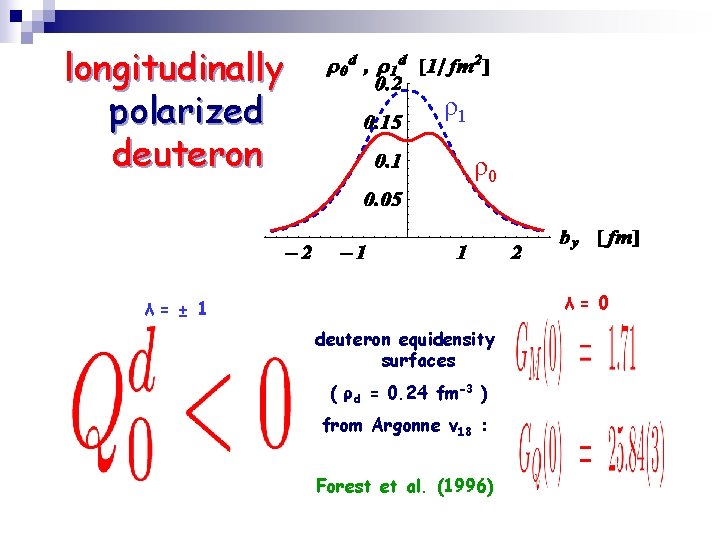
longitudinally polarized deuteron ρ1 ρ0 λ= ± 1 deuteron equidensity surfaces ( ρd = 0. 24 fm-3 ) from Argonne v 18 : Forest et al. (1996)

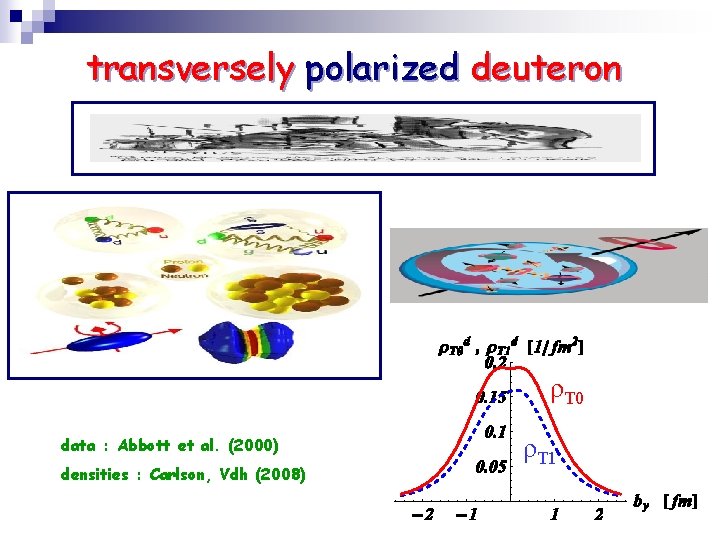
transversely polarized deuteron ρT 0 data : Abbott et al. (2000) densities : Carlson, Vdh (2008) ρT 1

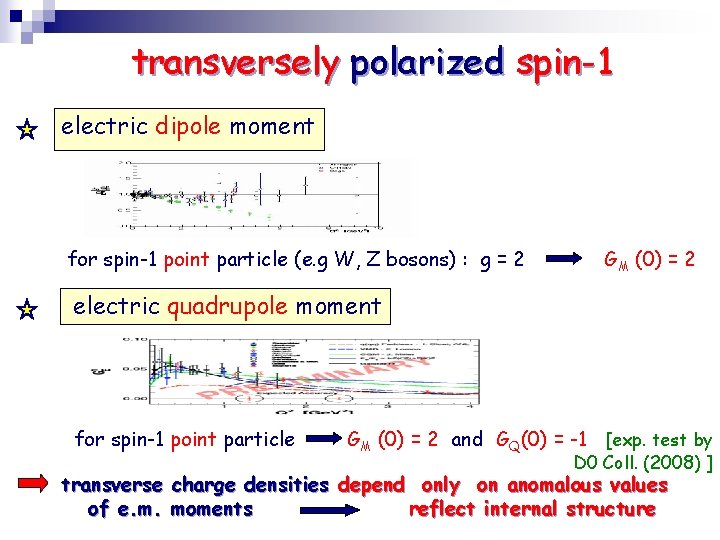
transversely polarized spin-1 electric dipole moment for spin-1 point particle (e. g W, Z bosons) : g = 2 GM (0) = 2 electric quadrupole moment for spin-1 point particle GM (0) = 2 and GQ(0) = -1 [exp. test by D 0 Coll. (2008) ] transverse charge densities depend only on anomalous values of e. m. moments reflect internal structure

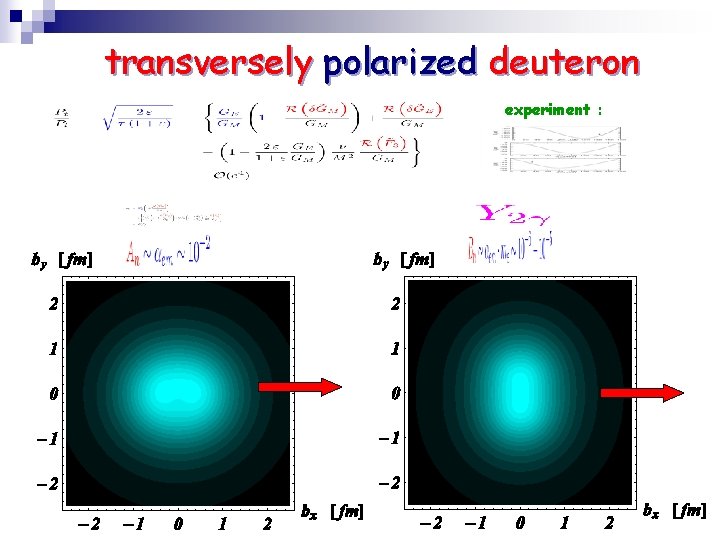
transversely polarized deuteron experiment :