HA 1 395 Parallel and Perpendicular Lines In

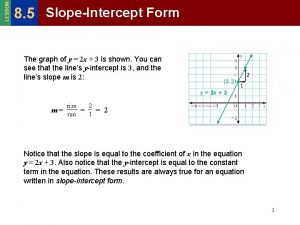
HA 1 -395: Parallel and Perpendicular Lines In this PPT, we will explore the wonderful world of parallel and perpendicular lines. Note: Parallel lines have the same slope. Example: y=2 x+5 is parallel to y=2 x-3. They both have a slope of 2. The only difference is that one line crosses the y-axis at 5 and the other line crosses the y-axis at -3 Perpendicular Lines have opposite ( switch the sign) reciprocal ( FLIP the fraction) slope: Like -2/3 and 3/2, or 3 and -1/3, or -3/4 and 4/3, or -5 and 1/5 th Example: y=2 x+5 has a slope of 2. In rise over run that is 2/1. A line that would be perpendicular to this line , and have a y intercept of -1, would have a slope of – ½ ( remember: opposite reciprocal). So the equation for this line would be y= -1/2 x-1. This line would form a perfect right angle ( like a plus sign) with y=2 x + 5. The third possibility is that lines are neither parallel or perpendicular, which is the “neither” choice. Example: y=2 x+5 and y=4 x-6 are neither parallel or perpendicular because their slopes have no relation ( they’re not the same or opposite reciprocal slopes).

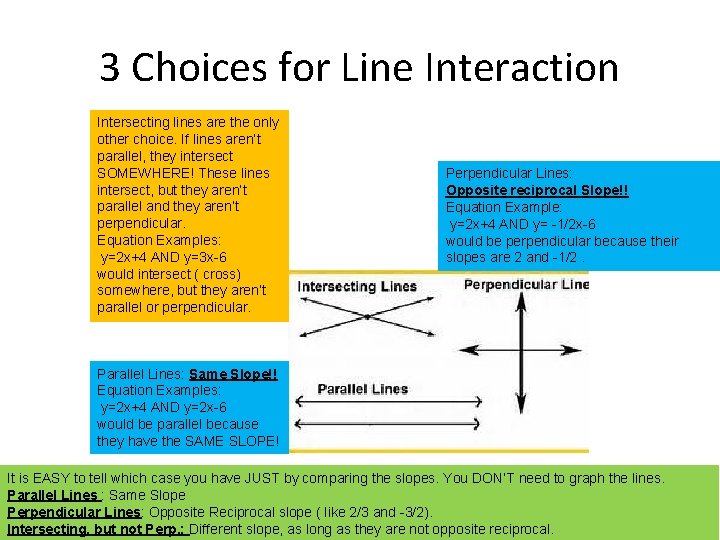
3 Choices for Line Interaction Intersecting lines are the only other choice. If lines aren’t parallel, they intersect SOMEWHERE! These lines intersect, but they aren’t parallel and they aren’t perpendicular. Equation Examples: y=2 x+4 AND y=3 x-6 would intersect ( cross) somewhere, but they aren’t parallel or perpendicular. Perpendicular Lines: Opposite reciprocal Slope!! Equation Example: y=2 x+4 AND y= -1/2 x-6 would be perpendicular because their slopes are 2 and -1/2. Parallel Lines: Same Slope!! Equation Examples: y=2 x+4 AND y=2 x-6 would be parallel because they have the SAME SLOPE! It is EASY to tell which case you have JUST by comparing the slopes. You DON’T need to graph the lines. Parallel Lines : Same Slope Perpendicular Lines: Opposite Reciprocal slope ( like 2/3 and -3/2). Intersecting, but not Perp. : Different slope, as long as they are not opposite reciprocal.

Parallel Lines • Let’s look at a few examples: – Find a line that is parallel to y=3 x-4 A) y=1/3 x +4 C) y= 4 x-3 B) y= -1/3 x-6 D) y= 3 x+7 Parallel Lines: Same Slope!! We need a line with a slope of 3. So D is the answer. - Find a line that is parallel to -2 x + y= 14 A) y= -2 x +4 C) y= 2 x-3 B) y= -2 x +14 D) y= 14 x+ 2 Parallel Lines: Same Slope!! Remember, we CAN’T pick out our slope if our equation is not in y=mx+b form. Use inverses and transform first to get y = 2 x +14. We need a line with a slope of 2. So C is the answer.

Parallel Lines • Let’s look at a few examples: – Find a line that is parallel to y=3 x-4 that passes through (-6, 12) careful if here • Be So. VERY we know we want a parallel line, then the slope is 3. So to thestart -6 in for x y=3 x + b for this parallel line. BUT, now we weputcan with and theto 12 find in for need b. y. • To find b, we use the point given ( -6, 12) and plug this x and y into our equation. 12 = 3 ( -6) + b => 12 = -18 + b => b = 30 Now we can write the FINAL equation that is parallel to y=3 x-4 and goes through point ( -6, 12) It is ……………. . y = 3 x + 30. YEAH!!!

Parallel Line practice problems. Now you try these 2 before we go onto perpendicular. Practice problems. 1. Find a line parallel to y= -2 x +3 that goes through ( 0, 6). 2. Jimmy is walking down a street that contains the points (-4, 4) and (4, 0). His sister is walking down a parallel street that goes through the point ( 6, 12). What is the equation for the parallel line that her street is on?

Parallel Practice Problem #1 1. Find a line parallel to y= -2 x +3 that goes through ( 0, 6). Well! We know it’s parallel, so let’s start with the slope intercept equation with just the slope in it. y = -2 x +b Look, we can’t put the b in yet because we don’t know where this line crosses the y axis. Now we know they gave us a point, let’s USE IT! Plug it in for x and y in the y=-2 x +b equation. We get 6 = -2(0) +b => 6 = 0 + b => 6 = b Now we can write the final equation of the line that is parallel to y=-2 x+3 and goes through (0, 6) It is………………y = -2 x + 6. Ta Dah!!!!

Parallel practice Problem #2 2. Jimmy is walking down a street that contains the points (-4, 4) and (4, 0). His sister, Jenny, is walking down a parallel street that goes through the point ( 6, 12). What is the equation for the line that her street is on? So, this is JUST LIKE #1, except we need to use our y 2 -y 1 over x 2 -x 1 skill to find slope before we do the same process as we did in #1. So let’s find slope first so we know what the parallel slope would be. ( -4, 4) and (4, 0) will give us 0 -4__ = -4 or -1 4 -(-4) 8 2 So the slope of Jimmy’s line is -1/2, that means the slope of Jenny’s line is ALSO -1/2. NICE!!!! Now we can begin to write her equation. y= -1/2 x +b. Now let’s find her y intercept!!

Parallel practice Problem #2 cont. So like said, now we know Jenny’s line is y= -1/2 x + b, but we don’t know her y intercept. Let’s USE WHAT THEY GAVE US!! They told us her line goes through (6, 12). Plug this x and y in! We go from y = -1/2 x + b to 12 = -1/2(6) +b 12 = -3 + b 15 = b Wow, not BAD! Now we can finish off Jenny’s equation. Jenny’s line, which is parallel to Jimmy, is ………………… y = -1/2 x + 15. C’mon, you can do that in your sleep! Now, let’s learn about perpendicular lines!

Perpendicular Lines • Perpendicular lines ( like a 90 degree cross) have slopes that are opposite and reciprocal, like 2/3 and -3/2 and -5 and 1/5 th. So if we’re given a slope it’s easy to find the perpendicular slope line. • Example 1: Choose the line Perpendicular line to y = 3 x – 6. A) y=1/3 x +4 B) y= -1/3 x-6 C) y= 4 x-3 D) y= 3 x+7 Perpendicular Lines: Opposite reciprocal Slope!! Our slope is 3, perp. Slope would be -1/3, so B is answer. • Example 2: Choose the line Perpendicular line to y = 3/4 x +9. A) y=-9 x+4 B) y= -3/4 x-6 C) y= 4 x-3 D) y= -4/3 x+7 Perpendicular Lines: Opposite reciprocal Slope!! Our slope is 3/4, perp. Slope would be -4/3, so D is answer.

Perpendicular Lines • Perpendicular lines ( like a 90 degree cross) have slopes that are opposite and reciprocal, like 2/3 and -3/2 and -5 and 1/5 th. So if we’re given a slope it’s easy to find the perpendicular slope, the part that needs work is to find the y intercept of our new line, the b. • Example: We have a line, y = 3 x – 6. We want the line that is perpendicular to this Look! line AND A lightpasses bulb should GO OFF and you through ( 12, 18). Let’simmediately find the slope of our new line. The slope need to realize we’re going to of this point in a minute!! y= 3 x-6 has slope of 3 use because m=3. So the slope of a line perpendicular to this line would have opposite, reciprocal slope. We go from 3 to opposite reciprocal slope of -1/3 rd. So we can START to write our perp. line equation, y = -1/3 x + b. Now let’s find that PESKY y intercept, which is the b, for our perp. Line.

Perpendicular Lines cont. Be VERY careful here to put the 12 in for x and the 18 in for y. So far we have y = -1/3 x + b. Now, we need to use the given point ( 12, 18) to find the b. LET’S PLUG IT IN! y = -1/3 x + b 18 = -1/3(12) + b 18 = -4 + b 22 = b Now we can write our final equation, the line that is perpendicular to y = 3 x – 6 is ……………. . y = -1/3 x + 22 Now you try a couple before you ACE your quiz. Practice problems: 1. Find the line perpendicular to y = 4 x – 8 that goes through ( 8, -4) 2. Jimmy is in the mall walking along looking in stores. His path goes through the points ( 0, -3) and ( 2, 3). Jenny is walking perpendicular to him along stores. Her path goes through the point ( 6, -6). What is the equation of the line Jenny is walking on?

Perpendicular Practice problem #1 1. Find the line perpendicular to y = 4 x – 8 that goes through ( 8, -4) Step 1: Find the perp. Slope. We go from a slope of 4 to the opposite reciprocal slope of -1/4 th. Step 2: BEGIN to write your equation now that we know our slope. y= -1/4 x + b Step 3: Find the y intercept of our line, the b. We need to plug in the given point of (8, -4). Let’s DO IT! -4 = -1/4(8) + b => -4 = -2 + b or -2=b Finally we can write our final equation. y= -1/4 x – 2. This line goes through (8, -4) and is perpendicular to y=4 x-8.

Perpendicular Practice problem #2 1. 2. Jimmy is in the mall walking along looking in stores. His path goes through the points ( 0, -3) and ( 2, 3). Jenny is walking perpendicular to him along stores. Her path goes through the point ( 6, -6). What is the equation of the line Jenny is walking on? Step 1: Find Jimmy’s slope using y 2 -y 1 x 2 -x 1 The points we have are (0, -3) and (2, 3), so our slope will be 3 -(-3) = 6 = 3 = slope of 3 2 -0 2 1 SO!! If the slope of Jimmy’s line is 3, the slope of the Jenny’s line perpendicular to this will be the opposite reciprocal of 3 or -1/3 rd. Step 2: Use the new slope to BEGIN to write the equation of the new line. So far we know Jenny’s line is y = -1/3 x + b Step 3: FIND the y intercept of Jenny’s line.

Perpendicular Practice problem #2 cont. Step 3: FIND the y intercept of Jenny’s line. We know they gave us a point (6, -6) on Jenny’s line we HAVEN’T used yet. Let’s PLUG IT IN and find b. y = -1/3 x + b -6 = -1/3(6) + b -6 = -2 + b -4 = b Step 4: Put the b we just found back into Jenny’s equation. y = -1/3 x + b now becomes y = -1/3 x -4 SO! To recap. Jimmy is walking along a slope of 3, and Jenny is walking along a line that is perpendicular to Jimmy with an equation of y = -1/3 x -4. NOW GO PASS THAT QUIZ!!