Gyrgy Dsa M Grazia Speranza Zsolt Tuza Improved

György Dósa – M. Grazia Speranza – Zsolt Tuza: Improved bounds for scheduling two uniform machines with known sum of the jobs University of Pannonia, University of Brescia, Hung. Academy of Science

Scheduling: some kind of combinatorial optimization We use three-field notation: α ׀ β ׀ γ, where α : machines: parallel, uniform (processing time is pi/s), … β : jobs: precedence constraints, release dates, due dates, preemption is allowed or not, … γ : objectives: makespan, (weighted) sum of completion times of jobs, number of not completed jobs, … (many practical applications, interesting, hard problems, …)

just an example: P 4 ׀׀ Cmax , i. e. • identical parallel machines, Cmax • no restrictions on jobs, • minimizing the maximum J 6 s J 1 6 J 2 M 1 M 2 J 3 3 M 3 J 5 compl. time (makespan) = Cmax J 4 • load: sum of proc. times of jobs assigned to the machine M 4 • s = smallest load this schedule is made by List Scheduling (Graham, ‘ 66)

Competitiveness (performance ratio) • We compare the „goodness” of an algorithm A to an optimal algorithm OPT • How many times can be A worse than OPT in the „worst case”, i. e. C(A) = sup { A(I) / OPT(I) }, where I is an arbitrary input (instance) ( for example, C(LS)= 2 - 1/m )

Lower bounds • Adversary: a very wrong sequence, for what no algorithm can perform well • Similar to a Maker-Breaker game: Maker = adversary (building a big makespan) Breaker = algorithm (enforcing a small makespan) • Optimality: if the lower bound touches the competitive ratio (we are happy if our algorithm is optimal)

(some) recent, and popular topics: • • Scheduling with machine cost (J. Noga, Cs. Imreh) Randomization (can help? ) Rejection (we can reject the job, but must pay penalty) Semi online problems: we know something, but not everything about the jobs, (or we have a buffer, or…) What is Known: sum, largest size, a range of sizes, order of the jobs, … now we will deal with this condition

so our problem is now: Q 2 ׀ Sum = S ׀ Cmax • two related machines, • only the sum of the sizes is known • the makespan is minimized

previous work: [1] Kellerer, Kotov, Speranza, Tuza: Semi online algorithms for the partition problem, Op. Res. Letters 21 (1997) a many times cited paper the main results: - three semi online versions of P 2 II Cmax, - three optimal algorithms with the same comp. ratio C=4/3, ( the pure online comp. ratio is C=3/2 (LS) )

case of 2 uniform machines, [2] Angelelli, Speranza, Tuza: known sum: Semi online scheduling on two uniform processors, Theor. Comp. Science 393 (2008), 211 -219. the paper provides: • three simple algorithms Q 2 ׀ Sum=S ׀ Cmax • lower bounds • optimality if s=1, and in two intervals (not everywhere opt. , or not proved to be opt. )

Previous (lower and upper) bounds from [2] these two intervals remained to be investigated better, where previous algorithms are not (or not proved to be) optimal

The case of the first interval: 1 < s < 1. 28 we have optimal algorithms for almost the whole interval

in the case of the first interval • the problem is solved by a „ladder” algoritm, (we will define it a little bit later) • only two „steps” are enough to get optimal ratio • the case of the other interval seems to be more difficult: - we still get optimal ratio for some subintervals - more steps are needed - we will show the results only for s=1. 5

lower the present results for s=1. 5: 1. 333 15/11=1. 3636 lower improved bounds upper 1. 4 Coal. Bas(1): 1. 4 (original) U Coal. Bas(2): 1. 3846 (better) P Coal. Bas(3): 1. 375 (better) P Coal. Bas(4): 1. 3721 (better) E Coal. Bas(5): 1. 3718 (better) R Coal. Bas(6): 1. 3714 (better) Coal. Bas(7): 1. 3715 (worse) (for further k? OPT = ? in case of other s? open questions)

How does an adversary work? (how to get 15/11) Suppose SUM=11+16. 5, we want to get loads 15 and 22. 5 resp. 15 22. 5 safe sets 11 S 0 (at least) Let J 1=1 if J 1 goes to M 2: 16. 5 12. 5 J 2=5 if J 2 goes to M 1: J 3=10, J 4=11. 5 5 4 6 s=1. 5 if J 2 goes to M 2: J 1 J 3=16. 5, J 4=5 in both cases: OPT=11, C ≥ 15, OK.

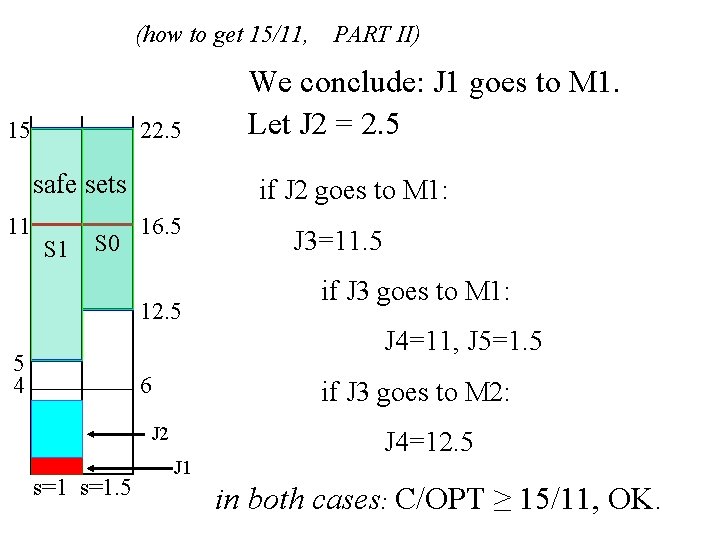
(how to get 15/11, 15 22. 5 safe sets 11 S 0 PART II) We conclude: J 1 goes to M 1. Let J 2 = 2. 5 if J 2 goes to M 1: 16. 5 12. 5 J 3=11. 5 if J 3 goes to M 1: J 4=11, J 5=1. 5 5 4 6 if J 3 goes to M 2: J 2 s=1. 5 J 1 J 4=12. 5 in both cases: C/OPT ≥ 15/11, OK.

(how to get 15/11, 15 22. 5 safe sets 11 S 0 16. 5 12. 5 5 4 6 J 3=4 J 1=1 J 2=2. 5 s=1. 5 PART III) We conclude: J 2 goes to M 2. Let J 3 = 4 if J 3 goes to M 2: J 4=16. 5 then: OPT=11, C ≥ 15, OK. We conclude: J 3 goes to M 1. *****THEN******* the last two jobs are J 4 = J 5 = 10, and OK.

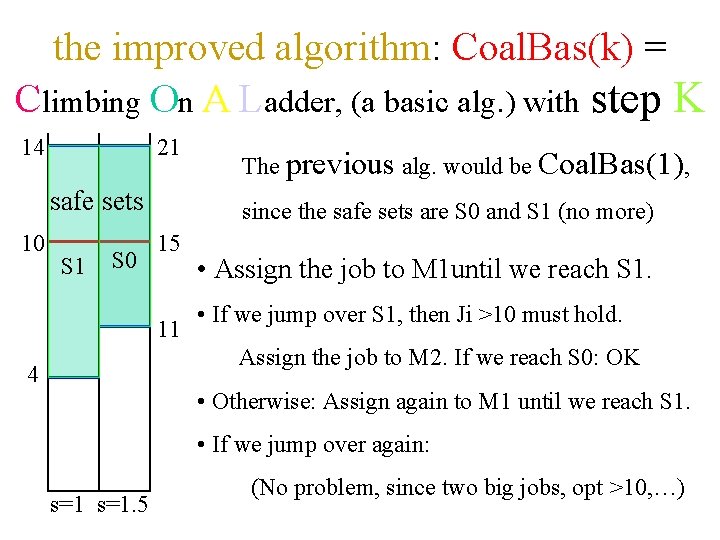
the improved algorithm: Coal. Bas(k) = Climbing On A Ladder, (a basic alg. ) with step K 14 21 safe sets 10 S 1 S 0 The previous alg. would be Coal. Bas(1), since the safe sets are S 0 and S 1 (no more) 15 11 • Assign the job to M 1 until we reach S 1. • If we jump over S 1, then Ji >10 must hold. Assign the job to M 2. If we reach S 0: OK 4 • Otherwise: Assign again to M 1 until we reach S 1. • If we jump over again: s=1. 5 (No problem, since two big jobs, opt >10, …)

the idea : by one more safe set: we get Coal. Bas(2), and C=36/26=1. 3846 < 1. 4 36 54 • Assign to M 2 while L 2 < 4 • If S 2 is reached: 26 S 1 S 0 39 - assign the next jobs to M 1 while L 1<11. - if S 1 is reached: OK (further jobs go to M 2) 29 - if the next job would jump over S 1: it is > 25 -assign it to M 2 11 15 S 2 s=1. 5 4 -if we reach S 0: OK (further jobs go to M 1) -if we jump over S 0: OK (further jobs go to M 1) • If S 2 is jumped over: the job is > 11, and so on…

How to define the safe sets? • we ensure that the proof will be correct • a simple recursion is applied • a better way? - If we get valid safe sets (nonnegative top and bottom, non overlapping safe sets) then this recursion is the best choice • what is the best choice of the safe sets if the recursion fails? • what is the best choice of parameter K?

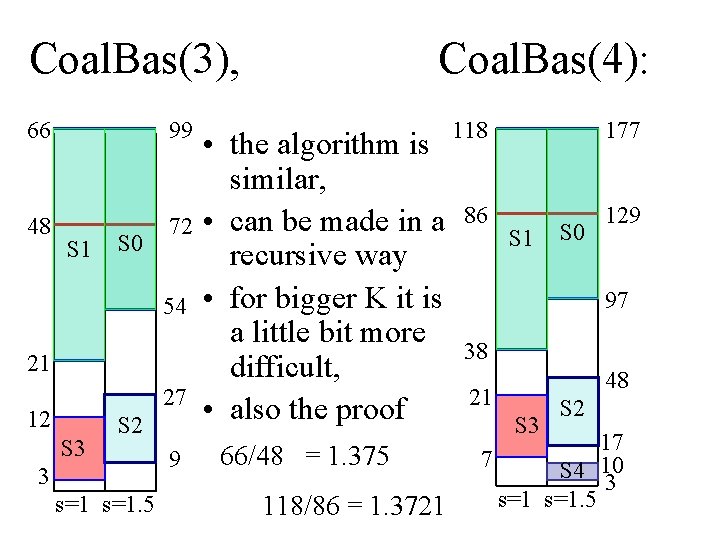
Coal. Bas(3), 66 99 48 72 S 1 S 0 54 21 27 12 S 3 S 2 3 s=1. 5 9 Coal. Bas(4): • the algorithm is similar, • can be made in a recursive way • for bigger K it is a little bit more difficult, • also the proof 66/48 = 1. 375 118/86 = 1. 3721 118 177 86 129 S 1 S 0 97 38 48 21 S 3 S 2 17 7 S 4 10 3 s=1. 5

• Coal. Bas(6): the best we can do in this way for s=1. 5 the best upper bound is 1. 3714 • • the lower bound is 1. 3636 Further improvements? Case of other s speeds? Better lower bound? (many open questions) Thank You for your kind attention!