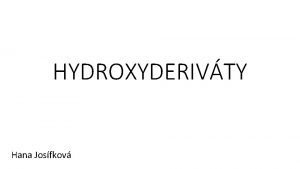Gymnzium T G Masaryka Hustopee Dukelsk nmst 7









- Slides: 11

Gymnázium T. G. Masaryka, Hustopeče , Dukelské náměstí 7 Vzdělávací oblast: Matematika a její aplikace Název: Hornerovo schema – algoritmus Autor: Ctirad Šedý Datum ověření, třída: 4. 2. 2013, Septima + 3. A (Seminář z matematiky) Stručná anotace: Slouží k hledání celočíselných kořenů rovnic vyššího řádu. Zároveň slouží K rozkladu mnohočlenu na součin. Tento materiál byl vytvořen v rámci projektu Inovace ve vzdělávání na naší škole V rámci OP Vzdělávání pro konkurenceschopnost

Hornerovo schema 1. 2. 3. Hledání kořenů kvadratické rovnice pomocí vztahů mezi kořeny Hledání celočíselných kořenů rovnic vyššího řádu než kvadratického Vytvoření tabulky z koeficientů rovnice a algoritmus hledání kořenů

Hledání kořenů kvadratické rovnice pomocí vztahů mezi kořeny Z učiva o kvadratických rovnicích je zřejmé, že pokud má normovaná rovnice celočíselné kořeny, lze je nalézt pomocí vztahů mezi kořeny kvadratické rovnice Z těchto i dalších příkladů je zřejmé, že pokud má normovaná kvadratická rovnice celočíselné kořeny, jsou tyto kořeny děliteli absolutního členu. (důležitý poznatek) Uvidíme, že tohoto poznatku ještě využijeme

Př. : Řešte pomocí vztahů mezi kořeny kvadratické rovnice Rozklad na kořenové činitele Jeden kořenový činitel Druhý kořenový činitel Jeden dvojnásobný kořenový činitel

Hledání celočíselných kořenů rovnic vyššího řádu než kvadratického i. Pokud má algebraická rovnice celočíselné kořeny, dá se rovnice zapsat ve tvaru součinu kořenových činitelů ii. S každým nalezeným celočíselným kořenem se sníží stupeň původní rovnice tak, že ji vydělíme kořenovým činitelem iii. Takto pokračujeme tak dlouho, až se dostaneme k jednotlivým kořenovým činitelům

V praxi to vypadá takto : Tento postup se ale jeví zdlouhavý a nepraktický a proto je nahrazen algoritmem pomocí tabulky s koeficienty rovnice

Vytvoření tabulky z koeficientů rovnice a algoritmus hledání kořenů 1 -2 -5 6 1 1 -1 -6 0 1 1 0 -6 1. 1 -1=0; 1. 0 -6=-6 -1 1 -2 -4 -1. 1 -1=2; -1. (-2)-6=-4 2 1 1 -4 2. 1 -1=1; 2. 1 -6=-4 -2 1 -3 0 3 1 0 1. 1 -2=-1; 1. (-1)-5=-6; 1. (-6)=0 -2. 1 -1=-3; -2. (-3)-6=0 3. 1 -3=0

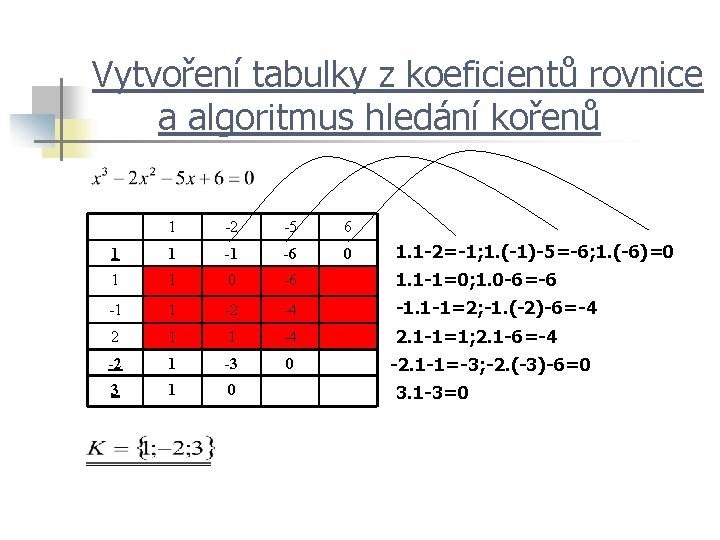
1 9 26 20 -24 -32 1 1 10 36 56 32 0 1 1 11 47 103 135 -1 1 9 27 29 -3 2 1 12 60 176 384 -2 1 8 20 16 0 -2 1 6 8 0 -2 1 4 0 -4 1 0

1 6 9 -4 -12 1 1 7 16 12 0 1 1 8 24 36 36 -1 1 6 10 2 2 2 1 9 34 80 160 -2 1 5 6 0 -2 1 3 0 -3 1 0

1 5 7 -1 -8 -4 1 1 6 13 12 4 0 1 1 7 20 32 36 -1 1 5 8 4 0 -1 1 4 4 0 2 1 6 16 -2 1 2 0 -2 1 0

A co na závěr? ? ? n n Doufám, že je algoritmus tvorby tabulky z koeficientů rovnice zřejmý Ne však vždy vede algoritmus tvorby tabulky k celočíselným kořenům. Pak tato rovnice (pokud jste počítali dobře) nemá buď celočíselné nebo reálné řešení.