Gymnzium Jozefa Gregora Tajovskho Bansk Bystrica STEREOMETRIA REZY

Gymnázium Jozefa Gregora Tajovského Banská Bystrica STEREOMETRIA REZY TELIES Tamás Fodor III. F 2010/2011

Čo je to stereometria Stereometria – priestorová geometria – vyšetruje geometrické útvary v priestore a ich vzťahy. � Úlohy riešené v stereometrii môžu byť dôkazové, výpočtové alebo konštrukčné. � Základnými stereometrickými pojmami sú bod, priamka, rovina. � Body označujeme veľkými tlačenými písmenami ( A, B, C, . . . ) � Priamky označujeme malými písanými písmenami (a, b, c, . . . ) � Roviny označujeme malými písmenami gréckej abecedy ( α, β, γ, . . . ) �

Niektoré základné stereometrické vzťahy � � � Ľubovoľnými dvomi navzájom rôznymi bodmi A, B v priestore prechádza práve jedna priamka. Ak priamka a je rovnobežná s priamkou b, priamka b je rovnobežná s priamkou c, tak aj priamka a bude rovnobežná s priamkou c. Rovina je určená: a) priamkou a bodom, ktorý neleží na nej b) dvomi rôznobežkami c) dvomi rôznymi rovnobežkami d) tromi bodmi, ktoré neležia na jednej priamke Ak priamka p je rovnobežná s niektorou priamkou p´ roviny ρ, je rovnobežná s rovinou ρ. Ak je priamka p kolmá ku dvom rôznobežným priamkam a, b roviny ρ, tak je kolmá k tejto rovine.

Vzájomné polohy útvarov 2 body sú rôzne bod patrí priamke bod patrí rovine 2 body sú totožné bod nepatrí priamke bod nepatrí rovine

Vzájomné polohy útvarov 2 priamky sú totožné 2 priamky sú rovnobežné 2 priamky sú rôznobežné 2 priamky sú mimobežné

Vzájomné polohy útvarov 2 ro viny sú 2 ro viny 2 ro s viny ú ro toto vno sú r žné bež ôzn né obe žné pria mka m k mka a je je r ôzn r pat o s v s n rov rí ro obe rov o b i e n žná vine ino ž o n u á u

Telesá HRANOL KOCKA IHLAN ZREZANÝ IHLAN KVÁDER VALEC

Telesá KUŽEĽ GUĽOVÁ VRSTVA ZREZANÝ KUŽEĽ GUĽOVÝ PÁS GUĽA GUĽOVÝ VRCHLÍK GUĽOVÝ VÝSEK

Rezy telies � Rez telesa rovinou je rovinný útvar, ktorého hranica je prienik hranice telesa s rovinou rezu. Hranica rezu telesa sa skladá z prienikov roviny so stenami telesa. � V 1: Ak je rovina rôznobežná s dvoma rovnobežnými rovinami, tak ich pretína v rovnobežných priamkach. � V 2: Ak je priamka rovnobežná s dvoma rôznobežnými rovinami, tak je rovnobežná aj s ich priesečnicou. � V 3: Nech každé dve z troch rovín sú rôznobežné. a) Ak dve z ich priesečníc sú rôznobežné, tak aj tretia prisečnica prechádza priesečníkom prvých dvoch. b) Ak dve z priesečníc sú rovnobežné, tak je s nimi rovnobežná aj tretia priesečnica.

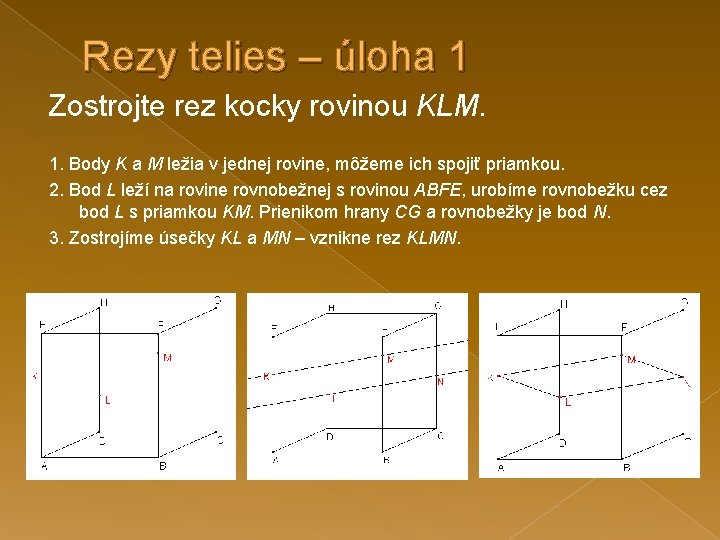
Rezy telies – úloha 1 Zostrojte rez kocky rovinou KLM. 1. Body K a M ležia v jednej rovine, môžeme ich spojiť priamkou. 2. Bod L leží na rovine rovnobežnej s rovinou ABFE, urobíme rovnobežku cez bod L s priamkou KM. Prienikom hrany CG a rovnobežky je bod N. 3. Zostrojíme úsečky KL a MN – vznikne rez KLMN.

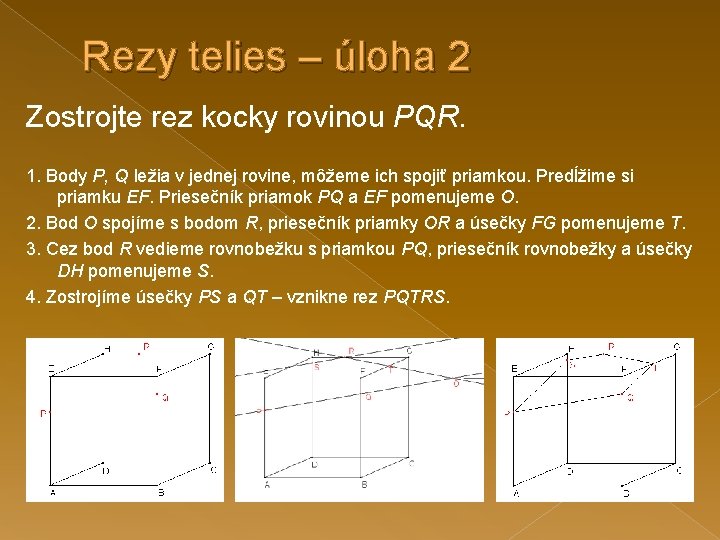
Rezy telies – úloha 2 Zostrojte rez kocky rovinou PQR. 1. Body P, Q ležia v jednej rovine, môžeme ich spojiť priamkou. Predĺžime si priamku EF. Priesečník priamok PQ a EF pomenujeme O. 2. Bod O spojíme s bodom R, priesečník priamky OR a úsečky FG pomenujeme T. 3. Cez bod R vedieme rovnobežku s priamkou PQ, priesečník rovnobežky a úsečky DH pomenujeme S. 4. Zostrojíme úsečky PS a QT – vznikne rez PQTRS.

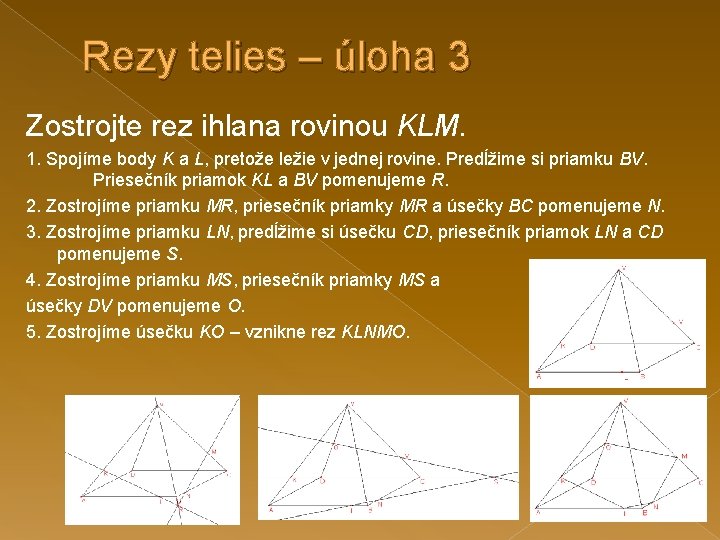
Rezy telies – úloha 3 Zostrojte rez ihlana rovinou KLM. 1. Spojíme body K a L, pretože ležie v jednej rovine. Predĺžime si priamku BV. Priesečník priamok KL a BV pomenujeme R. 2. Zostrojíme priamku MR, priesečník priamky MR a úsečky BC pomenujeme N. 3. Zostrojíme priamku LN, predĺžime si úsečku CD, priesečník priamok LN a CD pomenujeme S. 4. Zostrojíme priamku MS, priesečník priamky MS a úsečky DV pomenujeme O. 5. Zostrojíme úsečku KO – vznikne rez KLNMO.

Rezy telies – úloha 4 Zostrojte rez kocky rovinou PQR. 1. Body P a Q kolmo premietneme do roviny ABC, vzniknú body P´a Q´. Zostrojíme pomocnú rovinu PQP´. Zostrojíme priamku PQ a P´Q´. Ich priesečník pomenujeme O. Zostrojíme priamku OR. Priesečník priamky OE a úsečky BC pomenujeme S. 2. Zostrojíme rovnobežku s priamkou RS cez bod P. Priesečník rovnobežky s úsečkou GH pomenujeme T. Zostrojíme úsečku QT. Cez bod R vedieme rovnobežku s úsečkou QT, priesečník rovnobežky a úsečky AE pomenujeme U. 3. Zostrojíme úsečky QS a PU – vznikne rez PURSQT.

Zdroje informácií Božek, M. : Základy geometrie v priestore. SPN, Bratislava 1990 � Polák, J. : Přehled středoškolské matematiky. SPN, Praha 1983 � http: //www. zones. sk/studentske-prace/matematika/384 stereometria-telesa/ � http: //www. cbjanskanoc. ic. cz/Matematika. files/telesa 1. jpg � http: //www. cbjanskanoc. ic. cz/Matematika. files/Telesa 3. jpg 20. 5. 2011 – 16: 30 � � Obrázky: Cabri Geometry II Plus

ĎAKUJEM ZA POZORNOSŤ