GUC Spring 2012 1 Lecture 6 Linear Algebra

GUC - Spring 2012 1

Lecture 6 Linear Algebra (III) Linear Systems of Equations GUC - Spring 2012 2

Linear System of Equations • A system of m-linear equations in n variables x 1, x 2, . . . , xn has the general form (1) GUC - Spring 2012 3

Linear System of Equations • where the coefficients aij(i = 1, 2, . . . , m; j = 1, 2, . . . , n) • and the quantities bi • are all known scalars (numbers). GUC - Spring 2012 4

This is a Linear System GUC - Spring 2012 5

This is not a Linear System GUC - Spring 2012 6

Matrix Representation of a Linear System of Equations • Any linear system of the form (1) can be written in the matrix form AX = B GUC - Spring 2012 7

Matrix Representation of a Linear System of Equations • With A is the coefficient matrix GUC - Spring 2012 8

Matrix Representation of a Linear System of Equations X is the column of variables GUC - Spring 2012 9

Matrix Representation of a Linear System of Equations B is the column of constants GUC - Spring 2012 10

Example • Can be represented as GUC - Spring 2012 11

Example • The matrix form • Represents the system GUC - Spring 2012 12

Gauss Elimination Method • The method consists of four steps Ø 1. Construct an augmented matrix for the given system of equations. Ø 2. Use elementary row operations to transform the augmented matrix into an augmented matrix in row-reduced form. Ø 3. Write the equations associated with the resulting augmented matrix. Ø 4. Solve the new set of equations by back substitution. GUC - Spring 2012 13

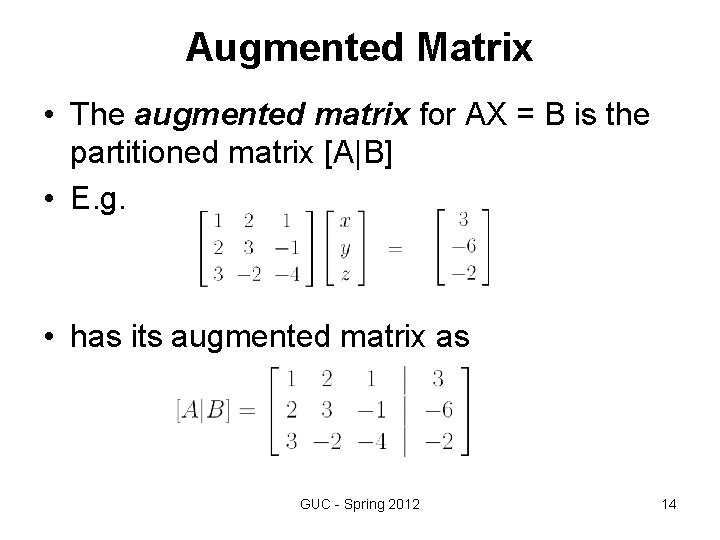
Augmented Matrix • The augmented matrix for AX = B is the partitioned matrix [A|B] • E. g. • has its augmented matrix as GUC - Spring 2012 14

Elementary Row Operations elementary row operations are : • 1 - Interchange any two rows in a matrix • 2 - Multiply any row of a matrix by a nonzero scalar • 3 - Add to one row of a matrix a scalar times another row of the same matrix GUC - Spring 2012 15

Row-Reduced Form • A matrix is in row-reduced form if it satisfies the following four conditions: 1. All zero rows appear below nonzero rows when both types are present in the matrix. 2. The first nonzero element in any nonzero row is 1. 3. All elements directly below (that is, in the same column but in succeeding rows form) the first (left- to- right) nonzero element of a nonzero row are 0. 4. The first nonzero element of any nonzero row appears in a later column (further to right) than the first nonzero element in any preceding row. GUC - Spring 2012 16

Example • Use Gaussian elimination to solve the system GUC - Spring 2012 17

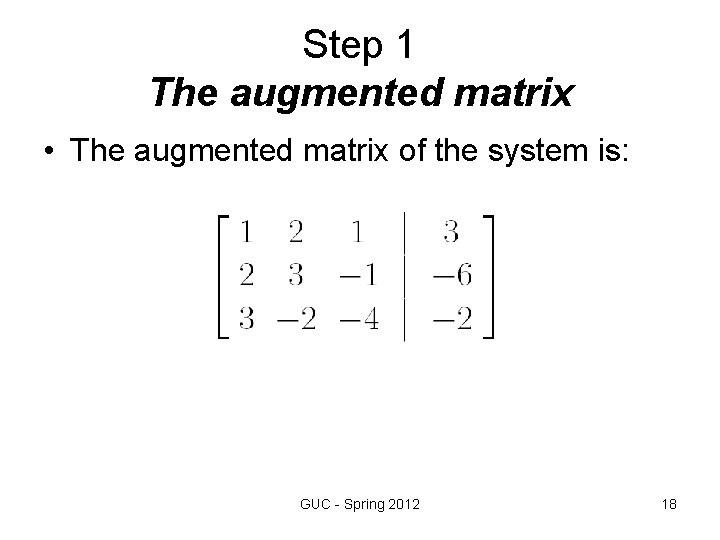
Step 1 The augmented matrix • The augmented matrix of the system is: GUC - Spring 2012 18

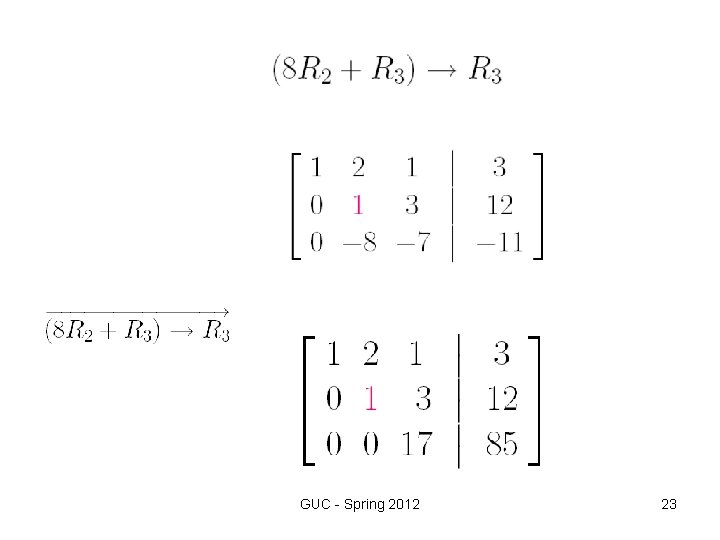
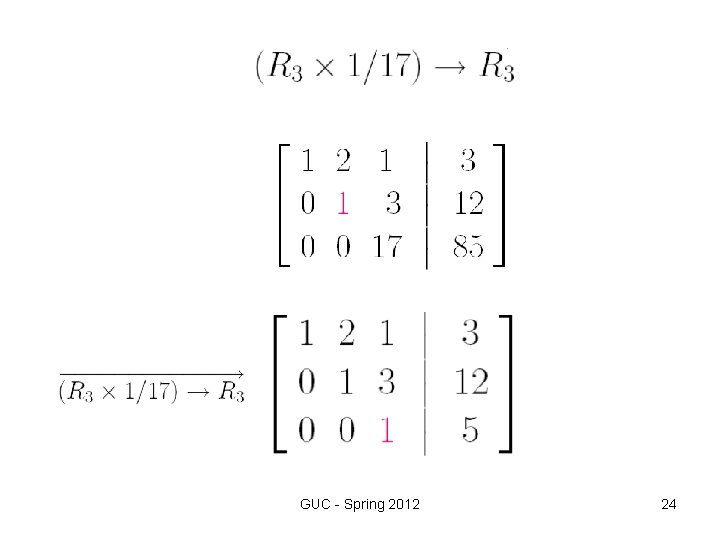
Step 2 Elementary row operations We use elementary row operations to transform the augmented matrix into row -reduced form as follows, GUC - Spring 2012 19

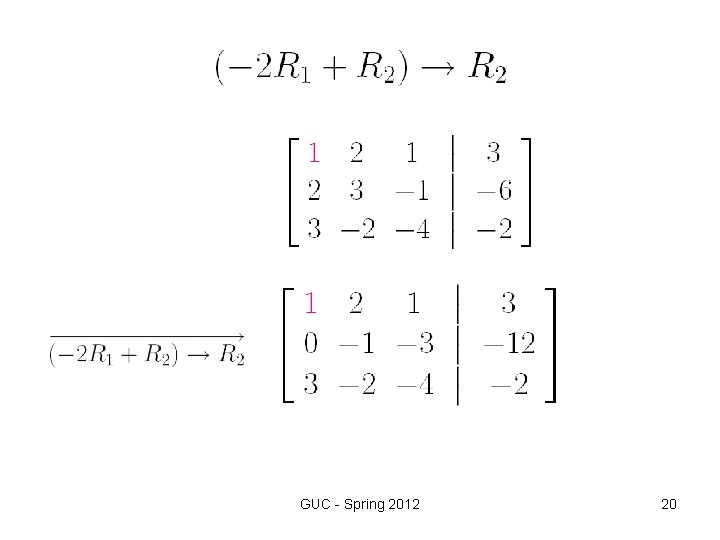
GUC - Spring 2012 20

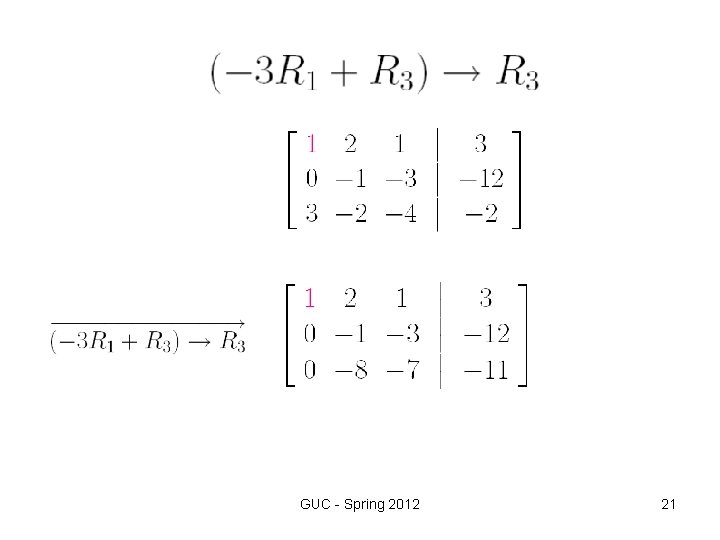
GUC - Spring 2012 21

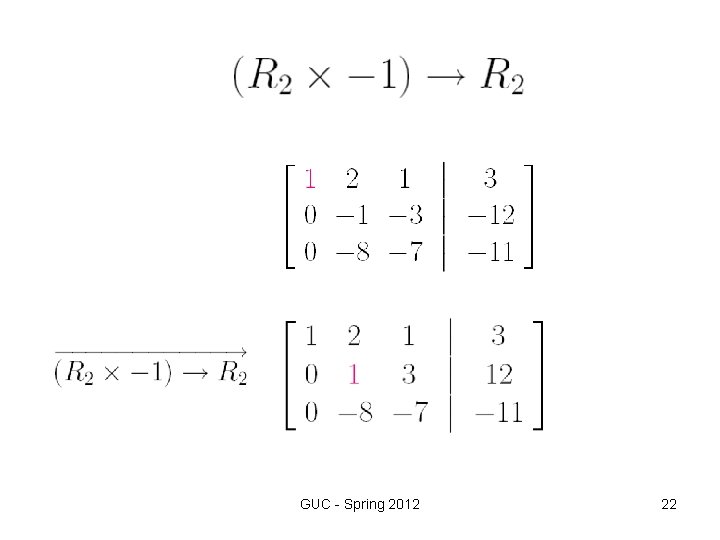
GUC - Spring 2012 22

GUC - Spring 2012 23

GUC - Spring 2012 24

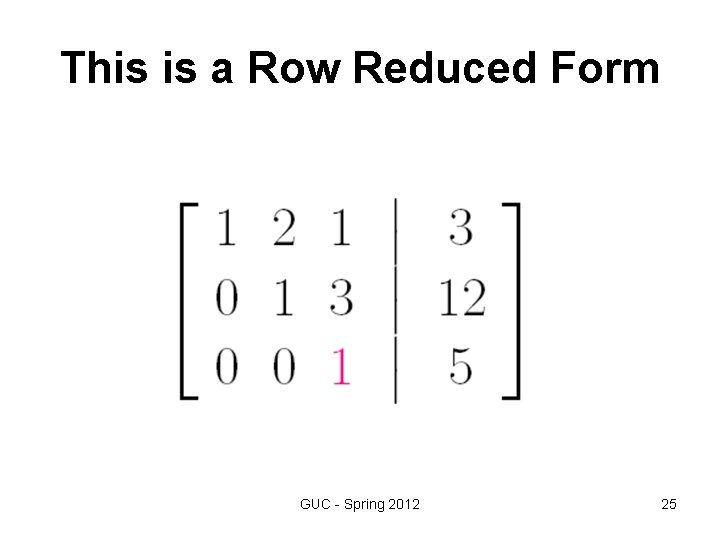
This is a Row Reduced Form GUC - Spring 2012 25

Step 3 The Resulting System • We write the equations of the resulting augmented matrix GUC - Spring 2012 26

Step 3 Writing the Resulting System • We write the equations associated with the resulting augmented matrix GUC - Spring 2012 27

Step 4 Solving the Resulting System • we Solve the derived set of equations by back substitution. • The third equation implies that z = 5, • Substituting in the second equation, we get y = 12 − 15 = − 3, • substituting with the values of z and y in the first equation, we get x = 4 GUC - Spring 2012 28

Example • Use Gauss elimination method to solve the linear system of equations GUC - Spring 2012 29

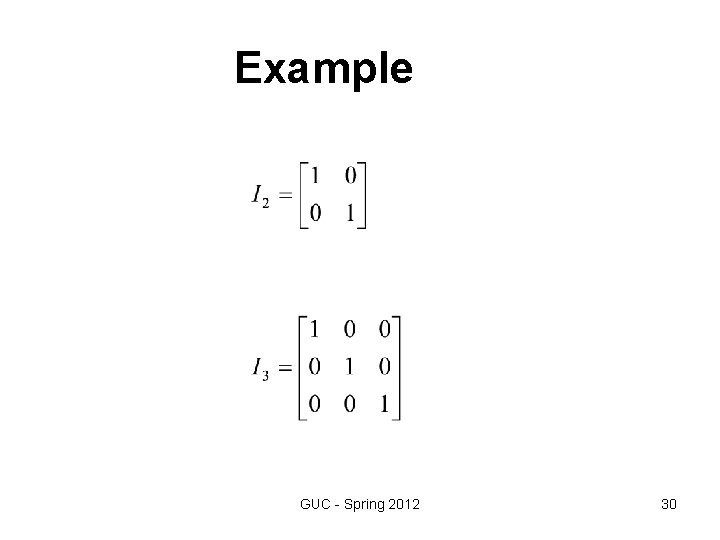
Example GUC - Spring 2012 30

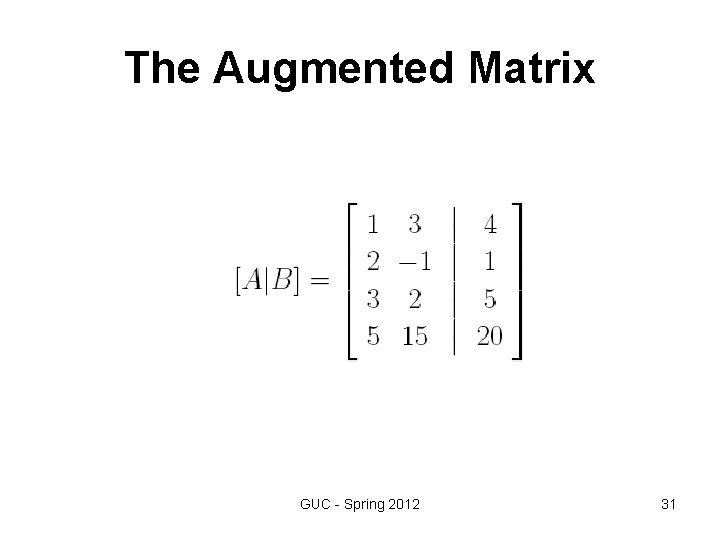
The Augmented Matrix GUC - Spring 2012 31

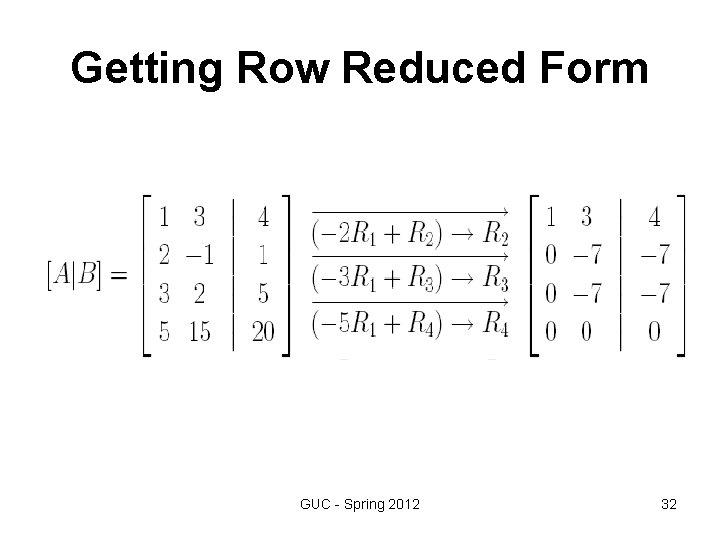
Getting Row Reduced Form GUC - Spring 2012 32

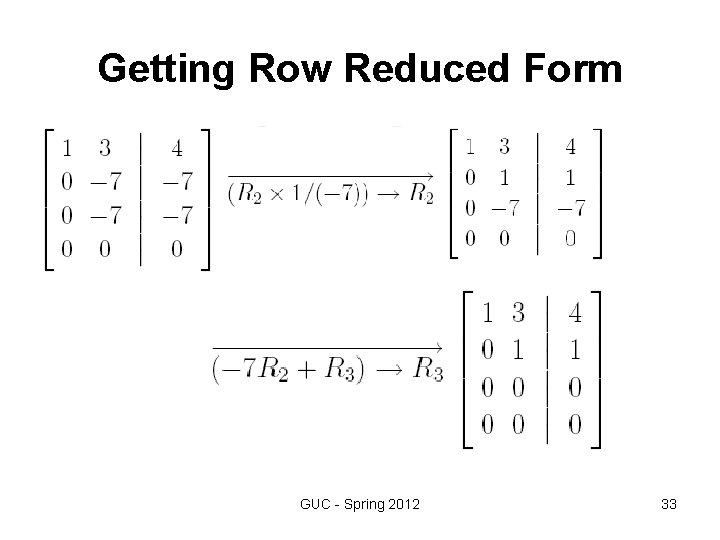
Getting Row Reduced Form GUC - Spring 2012 33

Writing the Resulting System • The resulting system of equations is GUC - Spring 2012 34

Solving the Equations • Solving the last system by substitution, we get the solution back • x = 1 and y = 1 GUC - Spring 2012 35

Example • Use Gauss elimination method to solve the linear system of equations GUC - Spring 2012 36

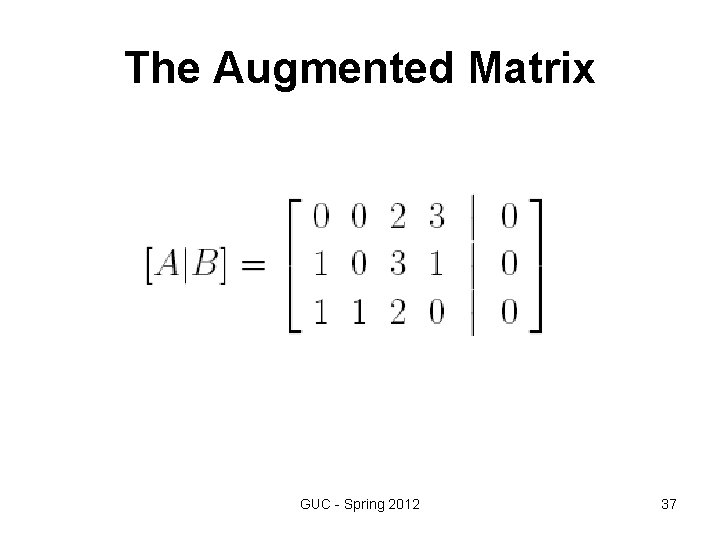
The Augmented Matrix GUC - Spring 2012 37

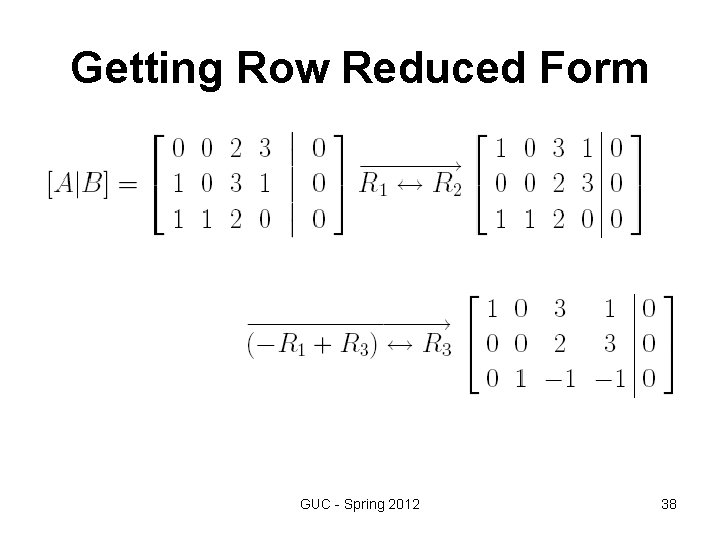
Getting Row Reduced Form GUC - Spring 2012 38

Getting Row Reduced Form GUC - Spring 2012 39

Writing the Resulting System GUC - Spring 2012 40

Important Note • Since the final system has the number of variables (4) greater than the number of equations (3), • then one of the variable will be arbitrary, • and the other variables will be found in terms of it. GUC - Spring 2012 41

Solving The Resulting System • The solution will be found in terms of x 4 as follows, GUC - Spring 2012 42

Note • Since x 4 is arbitrary, then the system has infinite number of solutions, depending on the value of x 4 • for example if you choose • Then, GUC - Spring 2012 43

Japan ! GUC - Spring 2012 44

No Comment GUC - Spring 2012 45