GSM CLONING GSM Global System for Mobile Communication

GSM CLONING

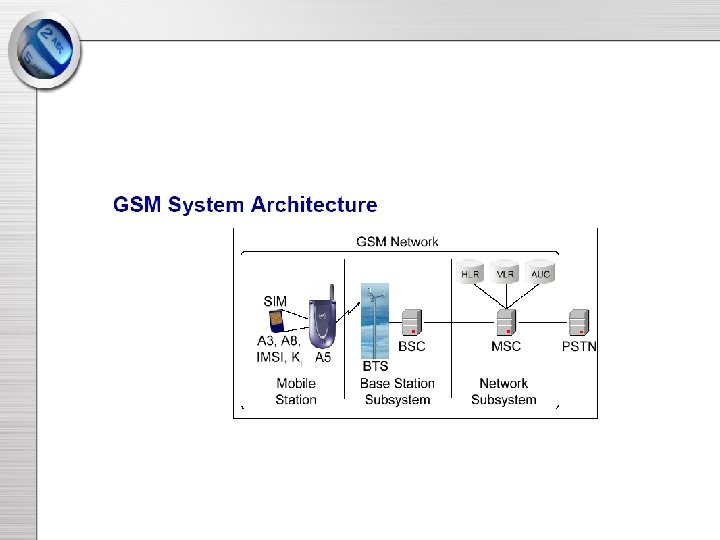
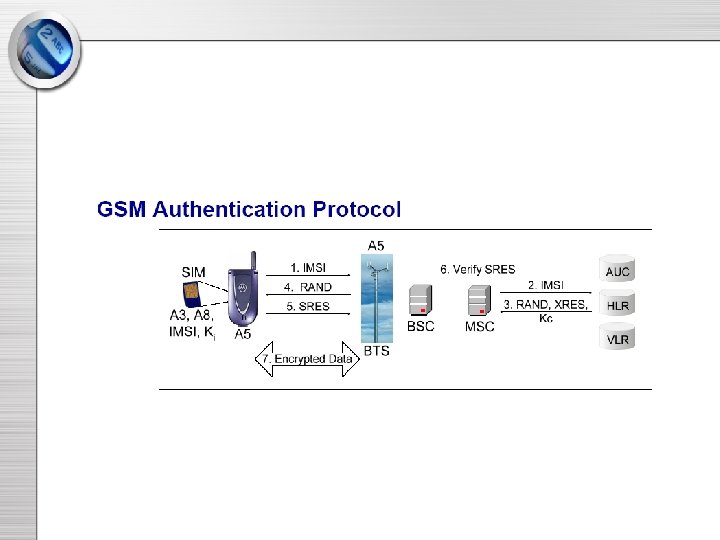
GSM (Global System for Mobile Communication) • Most widely used cellular mobile phone system. • First digital system to follow analog era. • Specification designed by GSM Consortium in secrecy. • Relied on Security by Obscurity. • Distributed on need-to-know basis. • Eventually leaked out and researchers have found many ways to break the GSM algorithms. • One way was breaking COMP 128 to retrieve the secret key from a SIM card.

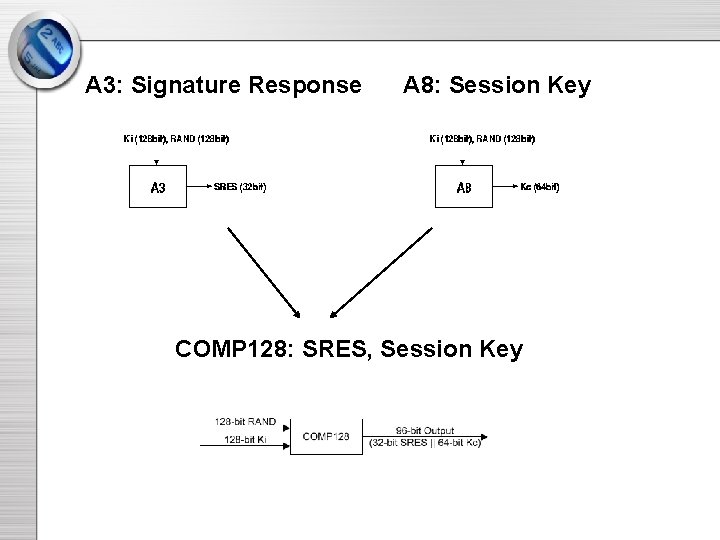
A 3: Signature Response A 8: Session Key COMP 128: SRES, Session Key

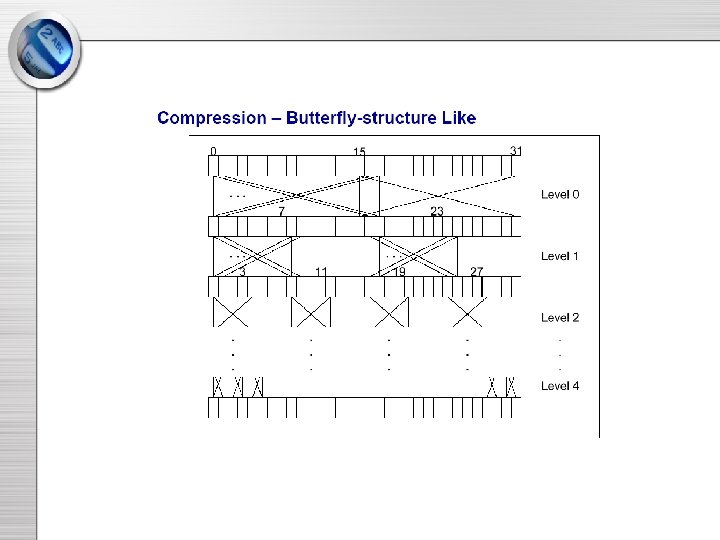
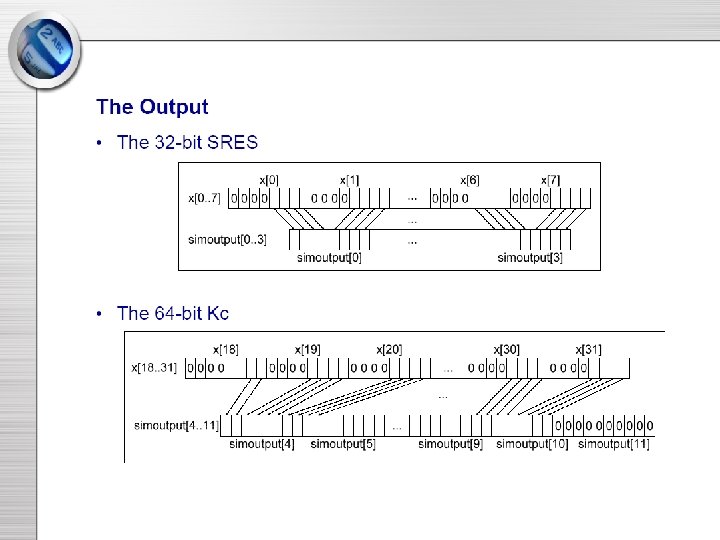
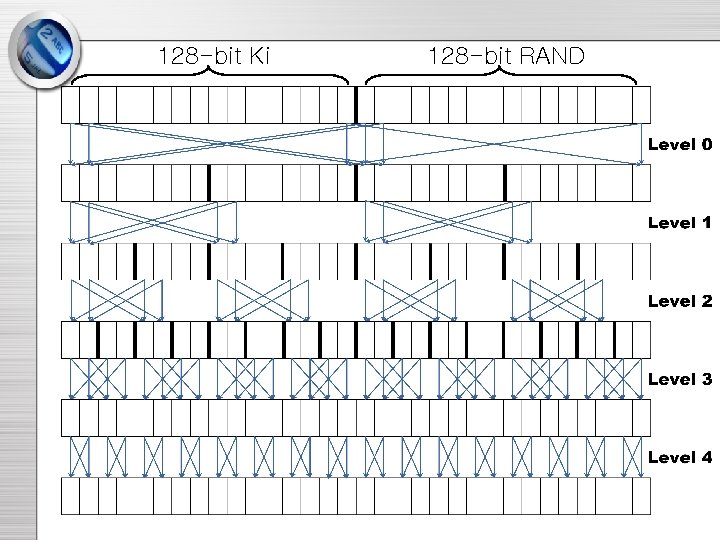
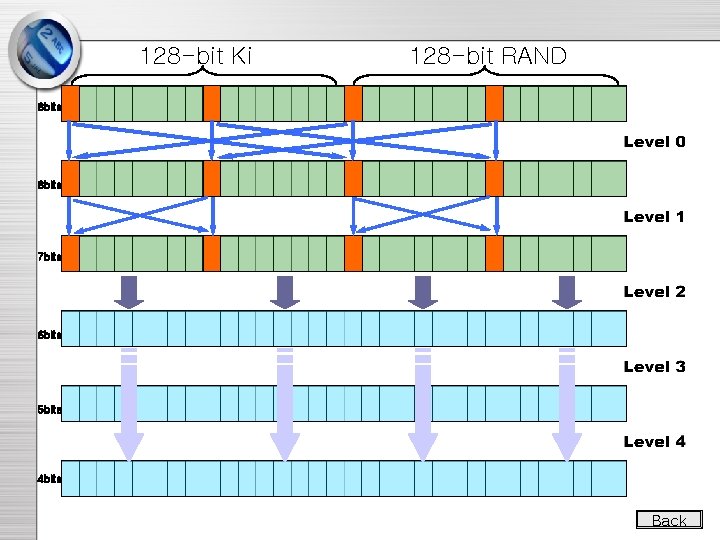
COMP 128 Pseudocode: • Input: 16 byte secret key, 16 byte RAND • Output: 4 byte SRES, 8 byte session key (simoutput[12]) • Load RAND into x[16… 31] • Perform the following 8 times – – Load secret key into x[0… 15] Compression Bits to Bytes Permutation (only on first 7 rounds) • Compress 16 bytes to 12 bytes (simoutput) • Return simoutput[ ]

Permutation: - Bits to Bytes - Only 4 bits in each entry - Example shows bits for x[0], x[1] gets bits 8, 25, 42, 59, 76, 93, 110, 127 Bits: 0 … 17 … 34 … 51 … 68 … 85 … 102 … Bytes: x[0] x[1] x[2] 119 …

What went wrong? • Design of a security cryptosystem should be under the Kerckhoffs’ principle. • GSM design committee kept all security specifications secret.

Attacks on COMP 128 • April 13, 1998: Marc Briceno (Director of the Smartcard Developer Association and two U. C. Berkeley researchers-David Wagner and Ian Goldberg The 128 bit Ki could be deduced by collecting around 150, 000 chosen RAND-SRES pairs. • May 2002: IBM Side-Channel attack (Partitioning Attack) 1000 random inputs, or 255 chosen inputs, or only 8 adaptively chosen inputs.

128 -bit Ki 128 -bit RAND

Crypto-attack by B. and G. • Information leaking. • A narrow “pipe” exists in COMP 128. bytes i, i+8, i+16, i+24 at the output of the 2 nd level depend only on bytes i, i+8, i+16, i+24 of the initial input. • Birthday paradox. • Differential technique.

128 -bit Ki 128 -bit RAND 8 bits 7 bits 6 bits 5 bits 4 bits Back

Crypto-attack cont. • • After the compression at level 1, The correlated 32 bits 28 bits. Transfer problem to Collision Attack. Alg. in the Random Oracle Model FINDCOLLISION 1. Choose 2. For each 3. do 4. If for some 5. then return 6. else return (failure)

Crypto-attack cont. 2 • The birthday paradox tells us if let our , we have probability at least 1/2 to get a collision. • The expectation of the number of queries: • How many chances can we have • The total expected queries to recover the entire 128 bit Ki is • How fast can we get? Computational ability of IC 6. 25 queries/s Totally recovery period: 7. 3 hours.

Improvement on B. and G. • Pre-compute 8 tables each has entries. • Every time we find a collision, just look up the corresponding tables to find the key. • Space requirements: GB • Limitation: The bottle-neck of recovery time is dominated by computational time of IC. This technique could decrease computational requirement of PC, but the whole time won’t decrease so much.

Evaluation of B. G. ’s Method • Pros: Easily to implement. High accuracy. Doesn’t have to physical access to the SIM card. • Cons: Slow: 7. 3 hours Spurious key Assumption Avoidance

Gains from B. G. ’s Attack • Necessity of the open design process • Importance of the first round • Aftermath of collisions

Partitioning Attack • Side channels: q q q Timing of operations Power consumption Electromagnetic emanations • Cardinal Principle: Relevant bits of intermediate cycles and their values should be statistically independent of the inputs, outputs and sensitive information.

Partitioning Attack cont. • Problems in COMP 128: q Huge correlation between MSB of R[0] and the beginning of the first compression. Figure q Substitution. Table look up operation. q Implementation in IC.

Partitioning Attack cont. 2 • Explanation for the correlation. Graph X[i]=T 0[K[i]+2*R[i]] and X[i+16]=T 0[2 K[i]+R[i]] K+2*26<256 • Example: Byte 1: All signals with R[0] in the range[0 -26] K+2*27>=256 and [155 -255] fell in one category and all signals K=202 or 203 with R[0] K=? in the range[27 -154] fell into the other. 2*K+105<512 and signals 2*K+106>=512 Byte 2: R[0] in the range[0 -105] fell in one category and [106 -255] signals fell into the other. K=203

Partitioning Attack cont. 3 • Efficiency q 1000 samples with random inputs q 256 chosen inputs q 8 adaptively chosen inputs

Future Improvements • COMP 128 -2 has replaced the COMP 128 to overcome some weakness • COMP 128 -3 is develop to generate 64 bits for Kc. • COMP 128 -4 is underdevelopment based on the 3 GPP(3 rd Generation Partnership Project) algorithm. (AES)

Input correlation for MSB of R[0]